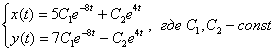Линейные неоднородные системы дифференциальных уравнений

Практически то же самое, только решение будет несколько длиннее.

Неоднородная система дифференциальных уравнений, которая в большинстве случаев может встретиться вам в задачах, имеет следующий вид:

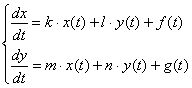
По сравнению с однородной системой в каждом уравнении дополнительно добавляется некоторая функция, зависящая от «тэ». Функции 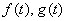могут быть константами (причем, по крайне мере одна из них не равна нулю), экспонентами, синусами, косинусами и т.д.

Пример 3

Найти частное решение системы линейных ДУ, соответствующее заданным начальным условиям

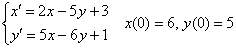
Решение: Дана линейная неоднородная система дифференциальных уравнений, в качестве «добавок» 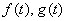выступают константы. Используем метод исключения, при этом сам алгоритм решения полностью сохраняется. Для разнообразия я начну как раз с первого уравнения.

1) Из первого уравнения системы выражаем:

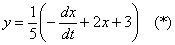
Это важная штуковина, поэтому я её снова замаркирую звёздочкой. Скобки лучше не раскрывать, зачем лишние дроби?

И еще раз заметьте, что из первого уравнения выражается именно «игрек» – через два «икса» и константу.

2) Дифференцируем по 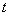обе части:

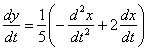
Константа (тройка) исчезла, ввиду того, что производная константы равна нулю.

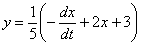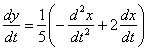3) Подставим и во второе уравнение системы :

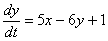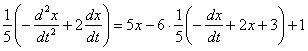
Сразу после подстановки целесообразно избавиться от дробей, для этого каждую часть уравнения умножаем на 5:

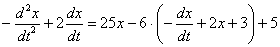
Теперь проводим упрощения:

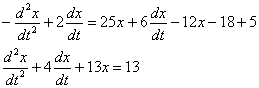
В результате получено линейное неоднородное уравнение второго порядка с постоянными коэффициентами. Вот, по сути, и всё отличие от решения однородной системы уравнений, разобранного в предыдущем параграфе.

Примечание: Тем не менее, в неоднородной системе иногда может получиться и однородное уравнение.

Найдем общее решение соответствующего однородного уравнения:

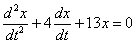
Составим и решим характеристическое уравнение:

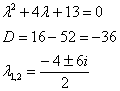
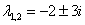– получены сопряженные комплексные корни, поэтому:
.

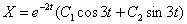Корни характеристического уравнения опять получились «хорошими», значит, мы на верном пути.

Частное решение неоднородного уравнения ищем в виде .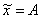
Найдем первую и вторую производную:

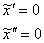
Подставим 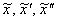в левую часть неоднородного уравнения:

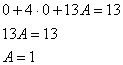
Таким образом: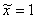

Следует отметить, что частное решение 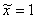легко подбирается устно, и вполне допустимо вместо длинных выкладок написать: «Очевидно, что частное решение неоднородного уравнения: ».

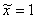В результате: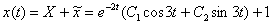

4) Ищем функцию 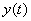. Сначала находим производную от уже найденной функции :

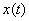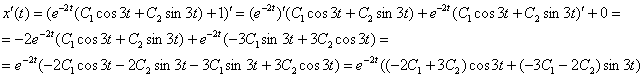
Не особо приятно, но подобные производные в диффурах приходится находить часто.

Шторм в самом разгаре, и сейчас будет девятый вал. Привяжите себя канатом к палубе.

Подставим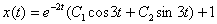
и 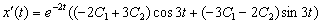в уравнение (*):

5) Общее решение системы:

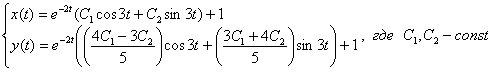
6) Найдем частное решение, соответствующее начальным условиям :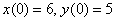

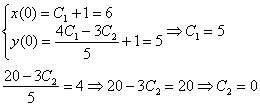
Окончательно, частное решение:

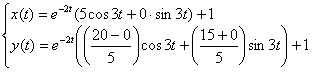
Вот видите, какая история со счастливым концом, теперь можно безбоязненно плавать на шлюпках по безмятежному морю под ласковым солнцем.

Ответ: частное решение: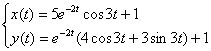

Кстати, если начать решать эту систему со второго уравнения, то вычисления получатся заметно проще (можете попробовать), но многие посетители сайта просили разбирать и более трудные вещи. Как тут откажешь? =) Пусть будут и более серьезные примеры.

Пример проще для самостоятельного решения:

Пример 4

Найти частное решение линейной неоднородной системы дифференциальных уравнений, соответствующее заданным начальным условиям

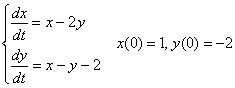
Данная задача решена мной по образцу Примера №1, то есть, из второго уравнения выражен «икс». Решение и ответ в конце урока.

В рассмотренных примерах я не случайно использовал различные обозначения, применял разные пути решения. Так, например, производные в одном и том же задании записывались тремя способами: 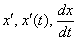. В высшей математике не нужно бояться всяких закорючек, главное, понимать алгоритм решения.

Метод характеристического уравнения (метод Эйлера)

Как уже отмечалось в начале статьи, с помощью характеристического уравнения систему дифференциальных уравнений требуют решить довольно редко, поэтому в заключительном параграфе я рассмотрю всего лишь один пример.

Пример 5

Дана линейная однородная система дифференциальных уравнений

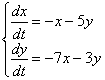
Найти общее решение системы уравнений с помощью характеристического уравнения

Решение: Смотрим на систему уравнений и составляем определитель второго порядка:

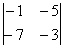
По какому принципу составлен определитель, думаю, всем видно.

Составим характеристическое уравнение, для этого из каждого числа, которое располагается на главной диагонали, вычитаем некоторый параметр :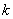

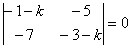
На чистовике, естественно, сразу следует записать характеристическое уравнение, я объясняю подробно, по шагам, чтобы было понятно, что откуда взялось.

Раскрываем определитель:

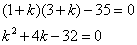
И находим корни квадратного уравнения:

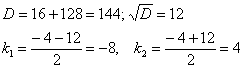
Если характеристическое уравнение имеет два различных действительных корня, то общее решение системы дифференциальных уравнений имеет вид:

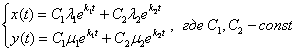
Коэффициенты в показателях экспонент 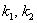нам уже известны, осталось найти коэффициенты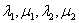

1) Рассмотрим корень 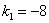и подставим его в характеристическое уравнение:

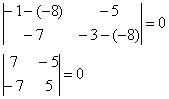
(эти два определителя на чистовике тоже можно не записывать, а сразу устно составить нижеприведенную систему)

Из чисел определителя составим систему двух линейных уравнений с двумя неизвестными:

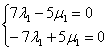
Из обоих уравнений следует одно и то же равенство:

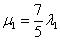
Теперь нужно подобрать наименьшее значение 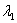, такое, чтобы значение 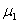было целым. Очевидно, что следует задать 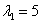. А если 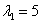, то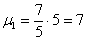

2) Всё аналогично. Рассмотрим корень 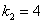и устно подставим его в характеристическое уравнение:

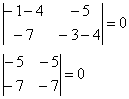
Из чисел определителя составим систему:

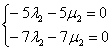
Из обоих уравнений следует равенство:

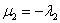
Подбираем наименьшее значение 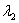, таким образом, чтобы значение 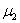было целым. Очевидно, что .

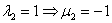Все четыре коэффициента 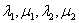найдены, осталось их подставить в общую формулу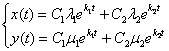

Ответ: общее решение: