Проверка шинных конструкций с жесткими опорами на электродинамическую стойкость
7.3.3.1. Шинную конструкцию, изоляторы которой обладают высокой жесткостью и неподвижны при КЗ, при расчете следует представлять как стержень с защемленными концами, имеющий основную частоту собственных колебаний.
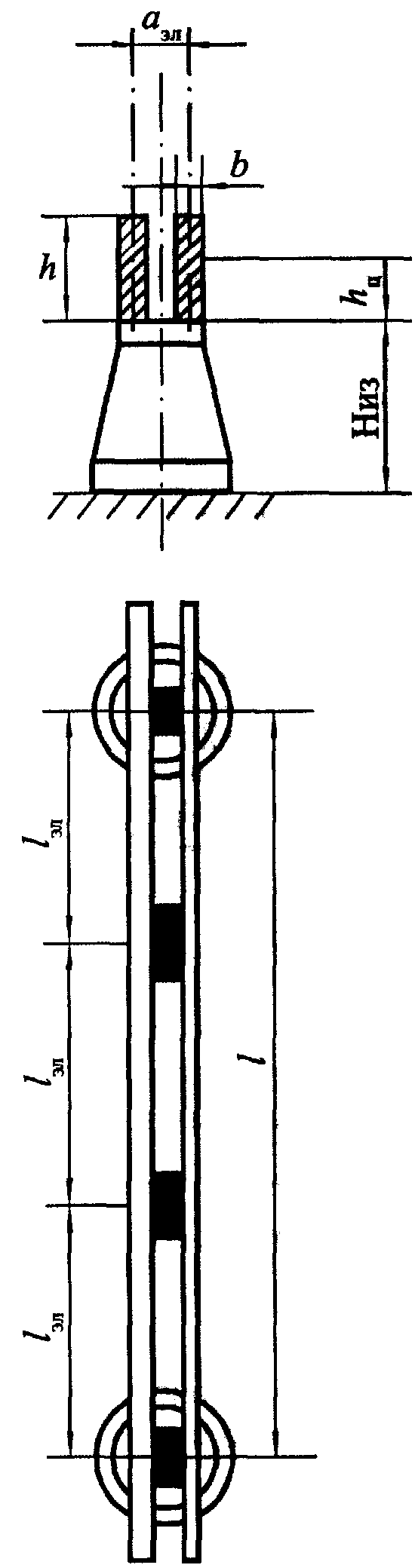
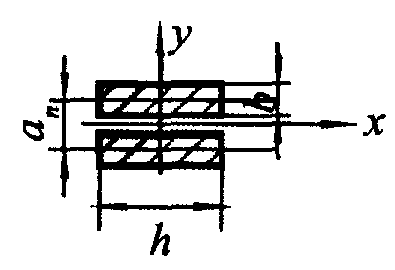
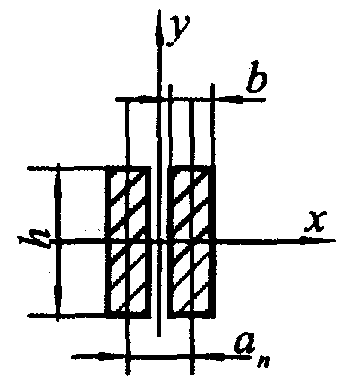
Рис. 7.4. Двухполосная шина
Таблица 7.4
Формулы для определения момента инерции J
и момента сопротивления W поперечных сечений шин
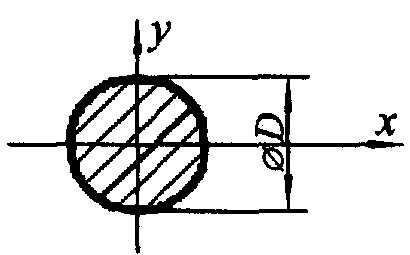
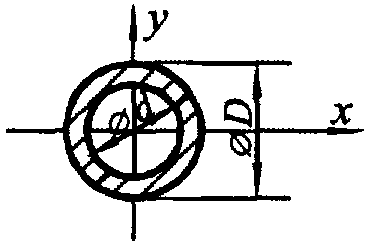
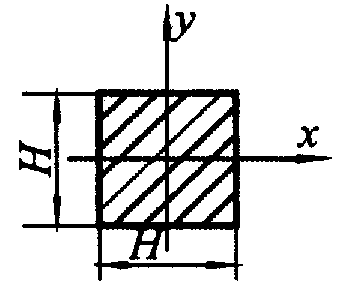
| Сечения шин | Расчетные формулы | |
| J, м4 | W, м3 | |
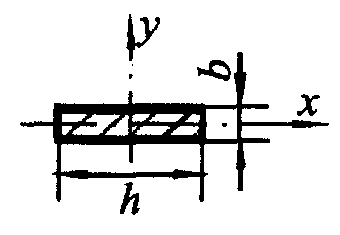 | 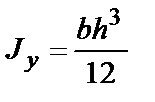 | 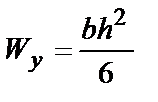 |
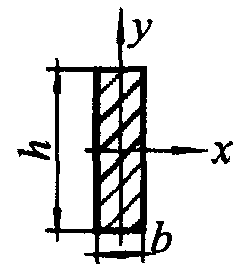 | 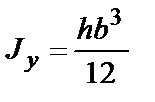 | 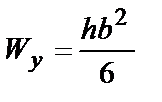 |
 | 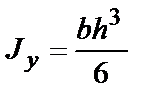 | 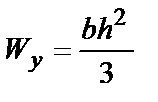 |
 | 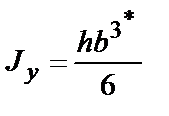 | 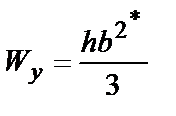 |
 | 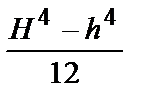 | 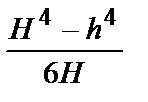 |
 | 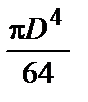 | 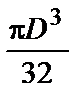 |
 | 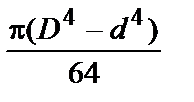 | 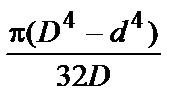 |
 | 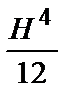 |  |
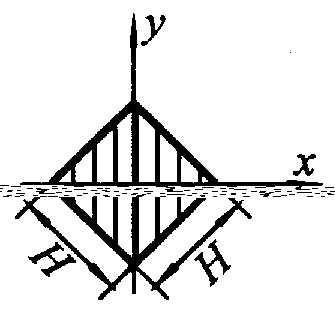 | 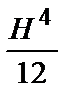 | 0,118Н3 |
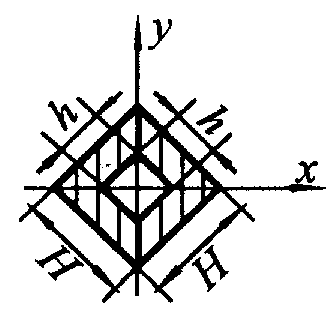 | 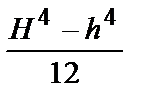 | 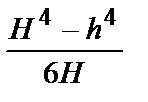 |
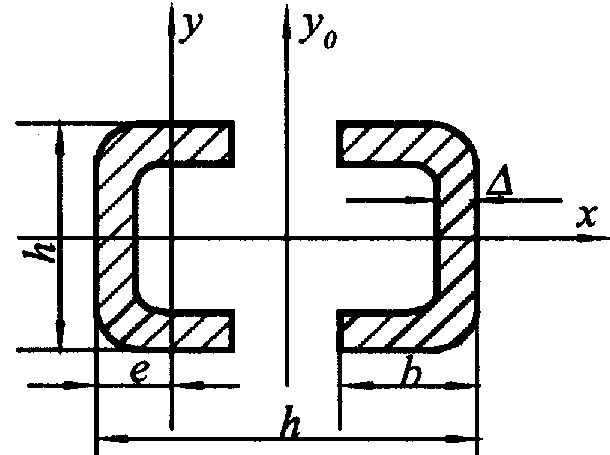 | Для одного элемента 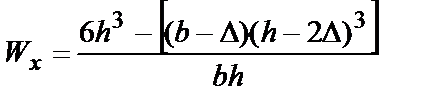 ; ; 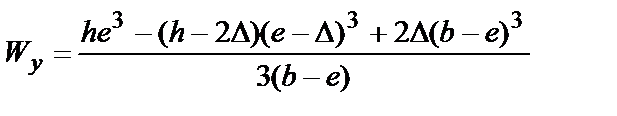 | |
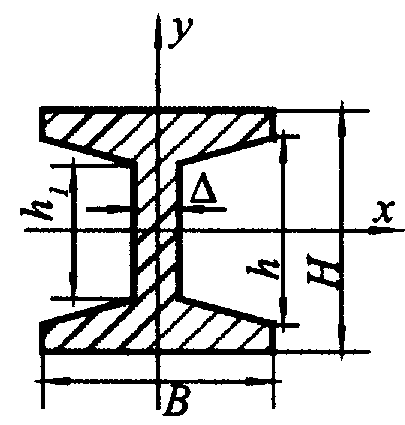 | 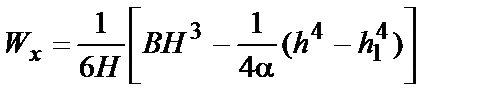 ; ; 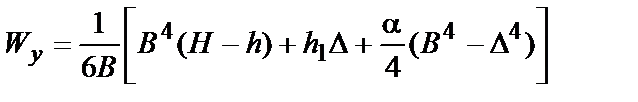 ; ; 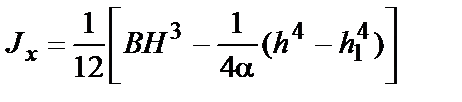 ; ; 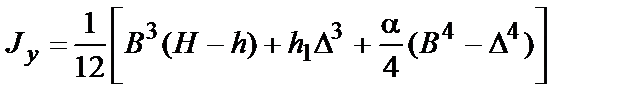 ; a»1/6 для стандартных двутавровых профилей ; a»1/6 для стандартных двутавровых профилей | |
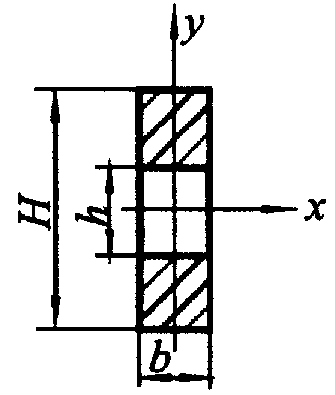 | 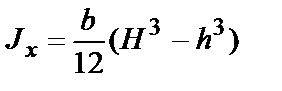 ; ; 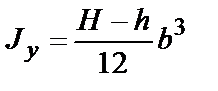 | 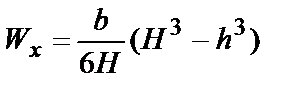 ; ; 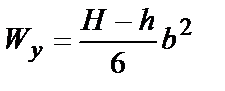 |
| Сечение прокатных профилей стандартных размеров | Приближенные формулы: двутавровый профиль на «ребро» 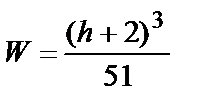 швеллерообразный (корытный) профиль на «ребро» швеллерообразный (корытный) профиль на «ребро» 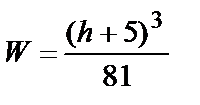 | |
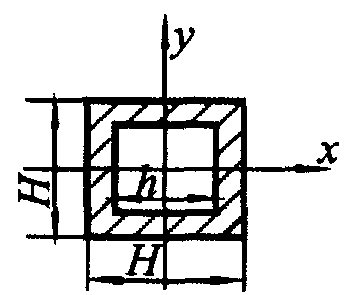
| Сечение любой формы | Ориентировочная оценка момента сопротивления относительно центральной оси: для сплошного симметричного сечения 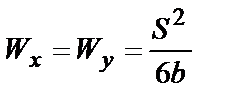 ; ; 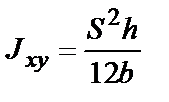 ; для полого симметричного сечения ; для полого симметричного сечения 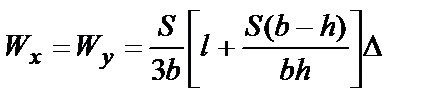 ; ; 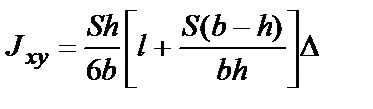 ; где S - площадь сечения; h, b - высота и ширина сечения соответственно; l - длина периметра; D - толщина стенки (для полого сечения) ; где S - площадь сечения; h, b - высота и ширина сечения соответственно; l - длина периметра; D - толщина стенки (для полого сечения) |
* Если прокладки приварены к обеим полосам пакета, моменты инерции и момент сопротивления принимаются равными: 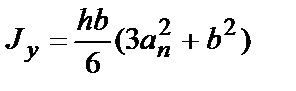 и
и 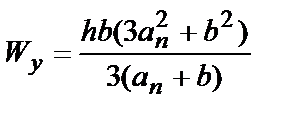 .
.
7.3.3.2. Максимальное напряжение в материале шин и нагрузку на изоляторы шинной конструкции, в которой шины расположены в одной плоскости, а изоляторы обладают высокой жесткостью, следует определять по формулам:
при трехфазном КЗ
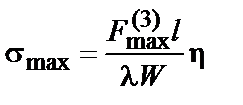 (7.19)
(7.19)
и
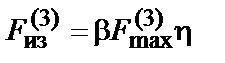 , (7.20)
, (7.20)
при двухфазном КЗ
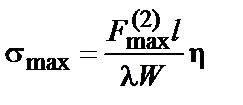 (7.21)
(7.21)
и
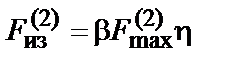 , (7.22)
, (7.22)
где h - коэффициент динамической нагрузки, зависящий от расчетной основной частоты собственных колебаний шины f1. Значения коэффициента для двухфазного и трехфазного КЗ в зависимости от отношения f1/fc (fc = 50 Гц) следует определять по графику на рис. 7.5.
Значения расчетной частоты собственных колебаний (f1) в герцах следует определять в соответствии с п. 7.3.3.4.
7.3.3.3. Максимальные нагрузки на проходные изоляторы следует определять по формуле
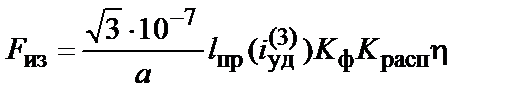 , (7.23)
, (7.23)
где lпр - расстояние от торца проходного изолятора до ближайшего опорного изолятора фазы, м.
7.3.3.4. Расчетную частоту собственных колебаний шины в герцах следует определять по формуле
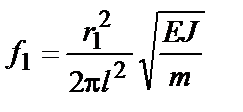 , (7.24)
, (7.24)
где Е - модуль упругости материала шины, Па;
J - момент инерции поперечного сечения шины, м4;
т - масса шины на единицу длины, кг/м;
r1 - параметр основной собственной частоты шины.
Значения параметра частоты зависят от типа шинной конструкции и представлены в табл. 7.1.
7.3.3.5. Максимальное напряжение в материале составных шин следует определять по формуле
smax = sф.max + sэл.max, (7.25)
где sф.max - максимальное напряжение в материале шин, которое следует определять в зависимости от вида КЗ по формуле (7.19) или (7.21);
sэл.max - максимальное напряжение в материале шины, которое следует определять по формуле
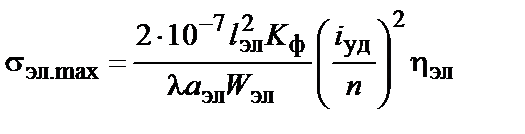 , (7.26)
, (7.26)
где hэл - коэффициент динамической нагрузки, зависящий от основной частоты (f1эл) собственных колебаний элементов составной шины, который следует определять по расчетному графику, приведенному на рис. 7.5.
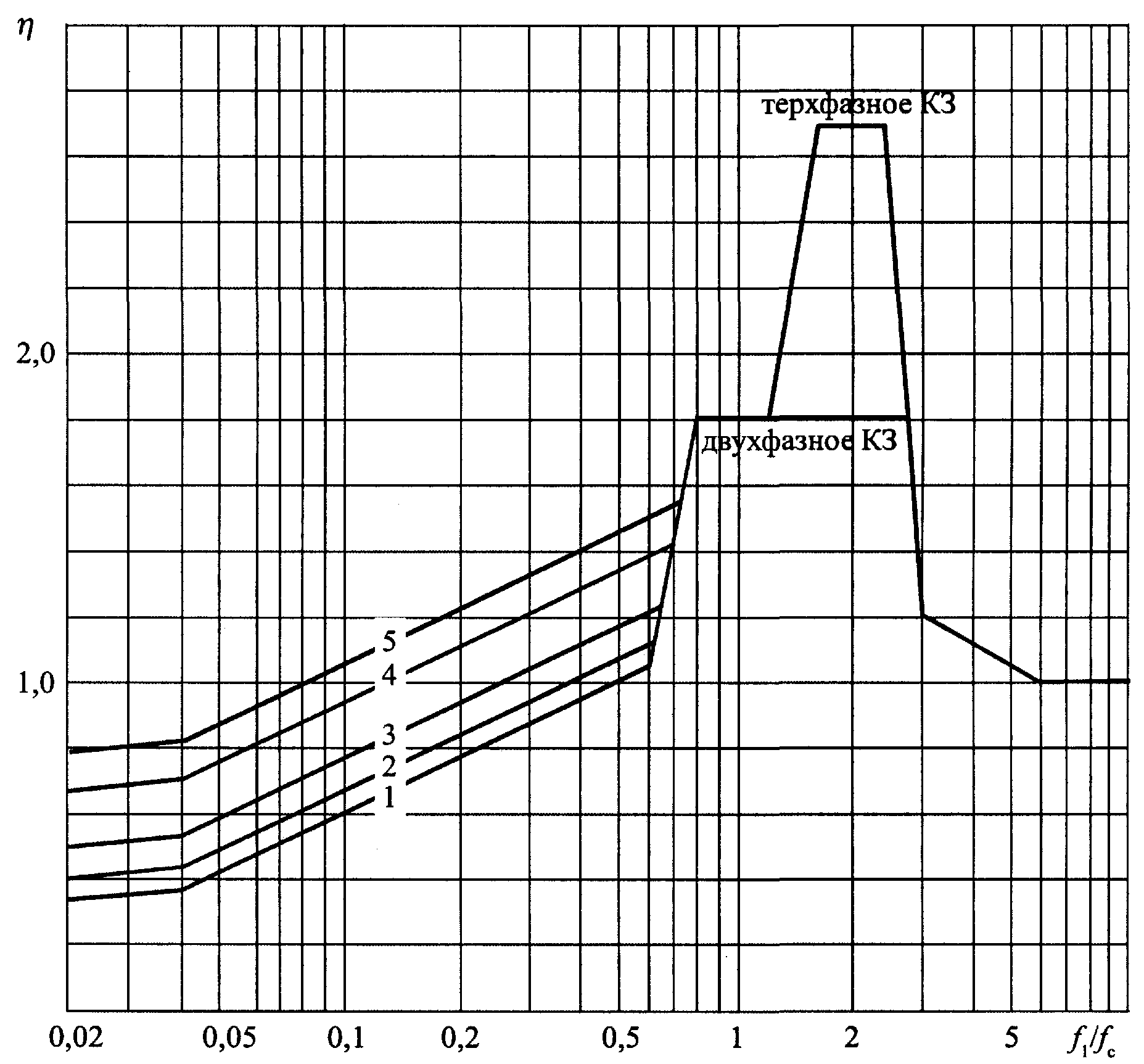
Рис. 7.5. Зависимость динамического коэффициента для изоляторов и шин от частоты собственных колебаний шины, где 1 при Куд ³ 1,60; 2 при Куд = 1,40;
3 при Куд =1,25; 4 при Куд = 1,10; 5 при Куд = 1,00
Расчетную основную частоту собственных колебаний элементов составной шины фазы в герцах следует определять по формуле
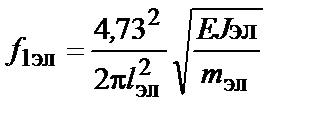 , (7.27)
, (7.27)
где lэл - длина пролета элемента шины между прокладками, м;
Jэл - момент инерции поперечного сечения элемента шин, м4;
тэл - масса элемента на единицу длины, кг/м;
аэл - расстояние между осями элементов составных шин (рис. 7.4), м.
7.3.3.6. Максимальные напряжения в материале шин и максимальные нагрузки на опорные и проходные изоляторы при расположении шин по вершинам треугольника (рис. 7.2, б, в, г) следует определять с учетом их пространственных колебаний по формулам
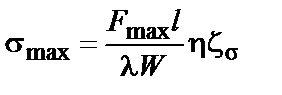 ; (7.28)
; (7.28)
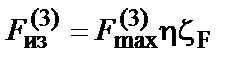 ; (7.29)
; (7.29)
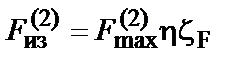 , (7.30)
, (7.30)
где W - меньший из двух моментов сопротивлений поперечного сечения шины (момента сопротивления WJ при изгибе в плоскости J и момента сопротивления Wt при изгибе шины в плоскости t) (рис. 7.2), м3;
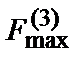 ,
, 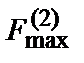 - электродинамические силы, определяемые соответственно по формулам (7.10) и (7.11);
- электродинамические силы, определяемые соответственно по формулам (7.10) и (7.11);
zs, zF - коэффициенты, значения которых для наиболее распространенных типов шинных конструкций (рис. 7.2, б, в, г) приведены в табл. 7.5.
Таблица 7.5
Значения коэффициентов zs и zF шинных конструкций
| Расположение | Эскиз | Значения | Значения коэффициента zs | |
| шин | конструкции на рис. 7.2 | коэффициента zF | для шин круглого и кольцевого сечения | для шин квадратного сечения |
| По вершинам прямоугольного равнобедренного треугольника | в | 0,95 | 0,95 | 1,16 |
| По вершинам равностороннего | б | 1,0 | 1,0 | 1,39 |
| треугольника | г | 1,0 | 1,0 | 1,21 |
