ТЕМА № 4. ПОЛОЖИТЕЛЬНЫЕ РАЦИОНАЛЬНЫЕ И
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
Понятие дроби. Сложение и вычитание положительных рациональных чисел. Умножение и деление рациональных чисел. Десятичные дроби и операции над ними. Понятие процента. Бесконечные десятичные дроби. Положительные действительные числа.
Литература: [1] с. 308-330, 335-339, [2] с. 148-152, [3] с. 180-228, [4] с. 82-89, [5] с. 152-165, [6] с.142-148.
ПОЛОЖИТЕЛЬНЫЕ РАЦИОНАЛЬНЫЕ И ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА (задания I уровня)
1А. Укажите значения истинности следующих высказываний:
а)  =
=  ; б)
; б)  >
>  ; в)
; в) 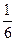 +
+  =
= 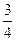 .
.
1Б. Верно ли, что:
а) 0,007 = 0,00 (7); б) 1,83 > 1,8; в) 1,(6) = 1 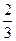 .
.
2А. Укажите значения истинности следующих высказываний:
а) 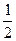 =
=  ; б)
; б)  >
> 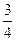 ; в)
; в) 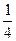 +
+ 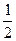 =
=  .
.
2Б. Верно ли, что:
а) 0,0612 = 0,06 (12); б) 1,05 > 1,1; в) 2,1 (25) = 2  .
.
3А. Укажите значения истинности следующих высказываний:
а) 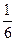 =
=  ; б)
; б) 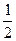 <
<  ; в) 1 –
; в) 1 –  =
=  .
.
3Б. Верно ли, что:
а) 0,09 = 0,0 (8); б) 21, (7) < 21,7; в) 2,8 (4) = 2  .
.
4А. Укажите значения истинности следующих высказываний:
а) 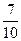 =
=  ; б)
; б)  >
>  ; в)
; в) 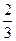 –
–  =
=  .
.
4Б. Верно ли, что:
а) 71,008 = 71,0 (08); б) 33,1 > 33, (1); в) 2, (3519) = 2  .
.
5А. Укажите значения истинности следующих высказываний:
а)  =
=  ; б)
; б)  <
<  ; в) 3
; в) 3  – 3
– 3  =
=  .
.
5Б. Верно ли, что:
а) 0,1375 = 0,1375 (0); б) 1,17 > 1,170; в) 8,291 (6) = 8  .
.
0А. Укажите значения истинности следующих высказываний:
а)  =
=  ; б)
; б)  <
<  ; в) 1
; в) 1 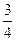 –
–  =
= 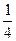 .
.
Решение:
а) НОК (7; 11) = 77, значит числа  и
и  можно привести к общему знаменателю 77:
можно привести к общему знаменателю 77:
 =
=  =
=  ;
;  =
=  =
=  ;
;  >
>  , т.е.
, т.е.  >
>  - истинное высказывание, значит
- истинное высказывание, значит  =
=  - ложное высказывание.
- ложное высказывание.
| б) | 8 | 2 | 12 | 2 | 8 = 23; 12 = 22 · 3; | |
| 4 | 2 | 6 | 2 | |||
| 2 | 2 | 3 | 3 | |||
| 1 | 1 |
НОК (8;12) = 23 · 3 = 24. Числа 8 и 12 можно привести к общему знаменателю 24:
 =
=  =
=  ;
;  =
=  =
=  ;
;  >
>  ;
;  >
>  ,
,
значит,  <
<  - истинно.
- истинно.
в)  –
–  =
=  –
–  = (1 – 1) + (
= (1 – 1) + ( 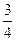 –
–  ) = 0 +
) = 0 + 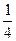 =
= 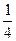 ,
,
т. е.  –
–  =
= 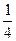 - истинно.
- истинно.
0Б. Верно ли, что:
а) 3,87 (5) = 3,87 (50); б) 23,05 < 23, (05); в) 7,91 (6) = 7  .
.
Решение:
а) Для проверки истинности записанного равенства переведем дроби в обыкновенные.
Чтобы смешанную периодическую дробь перевести в обыкновенную, нужно в числителе записать разность между числом, записанным цифрами, стоящими до второго периода, и числом, записанным цифрами предпериода. В знаменателе записываем число, состоящее из стольких 9, сколько цифр в периоде, и стольких 0, сколько цифр в предпериоде.
3,87 (5) = 3 +  =
=  ; 3,87 (50) = 3 +
; 3,87 (50) = 3 +  =
=  ;
;
 ≠
≠  .
.
Ответ: 3,87 (5) ≠ 3,87 (50).
б) Для проверки истинности неравенства переведем дроби в обыкновенные: 23,05 =  .
.
Чтобы чистую периодическую дробь перевести в обыкновенную, необходимо в числителе записать число, образованное цифрами периода, а в знаменателе – столько 9, сколько цифр в периоде. 23,05 = 
Сравниваем дроби  и
и 
Так как целые части равны, сравниваем дробные:  и
и  ;
;
 <
<  (т.к. 1 · 99 < 5 · 20);
(т.к. 1 · 99 < 5 · 20);  <
< 
Ответ: 23,05 < 23, (05).
в) Переведем десятичную дробь 7,91(6) в обыкновенную:
7,91(6) = 7 +  =
=  =
=  ;
;
Значит, 7,91(6) =  - верно.
- верно.
Ответ: 7,91(6) =  .
.
ПОЛОЖИТЕЛЬНЫЕ РАЦИОНАЛЬНЫЕ И ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА (задания II уровня)
1А. Представьте десятичные дроби в виде обыкновенной:
а) 0,125; б) 0,0(3); в) 6,(435).
1Б. Для данного множества запишите подмножества, состоящие из: а) рациональных чисел; б) иррациональных чисел; в) целых чисел.
А={  ; 1,666…; 2
; 1,666…; 2 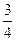 ; 1,521131313…;
; 1,521131313…;  ;
;  ; 5,1234167…, 0,27000…; 6,000…; 2,313133313…}
; 5,1234167…, 0,27000…; 6,000…; 2,313133313…}
2А. Представьте десятичные дроби в виде обыкновенной:
а) 9,126; б) 2,(2519); в) 2,1(3).
2Б. Для данного множества запишите подмножества, состоящие из: а) рациональных чисел; б) иррациональных чисел; в) целых чисел.
В={5,111…; 2,311331133113…;  ;
;  ;
;  ; 3,000…; 1
; 3,000…; 1  ; 0,1231757…;
; 0,1231757…;  }.
}.
3А. Представьте десятичные дроби в виде обыкновенной:
а) 43,375; б) 0,1(2); в) 0,(571428).
3Б. Для данного множества запишите подмножества, состоящие из: а) рациональных чисел; б) иррациональных чисел; в) целых чисел.
С={7,(5);  ; 0,75; 5,666…;
; 0,75; 5,666…;  ;
;  ;
;  ; 1,7121314…; 0,(83)}.
; 1,7121314…; 0,(83)}.
4А. Представьте десятичные дроби в виде обыкновенной:
а) 0,1375; б) 0,(31); в) 4,6(3).
4Б. Для данного множества запишите подмножества, состоящие из: а) рациональных чисел; б) иррациональных чисел; в) целых чисел.
Д={ 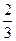 ; 4,(2); 7,00…;
; 4,(2); 7,00…;  ; 0,2(34); П;
; 0,2(34); П;  ;
;  ;
;  ; 0,121314…}
; 0,121314…}
5А. Представьте десятичные дроби в виде обыкновенной:
а) 3,075; б) 0,2(35); в) 17,(22).
5Б. Для данного множества запишите подмножества, состоящие из: а) рациональных чисел; б) иррациональных чисел; в) целых чисел.
Е={  ;
;  ; 2,1(3); 45
; 2,1(3); 45 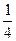 ;
;  ; 11,1212…; 25,(2); 71,1444…}.
; 11,1212…; 25,(2); 71,1444…}.
0А. Представьте десятичные дроби в виде обыкновенной:
а) 7,001; б) 0,5(8); в) 6,(12).
Решение:
а) 7,001 =  ;
;
б) Для того, чтобы смешанную периодическую дробь перевести в обыкновенную, нужно в числителе записать разность между числом, записанным цифрами, стоящими до второго периода, и числом, записанным цифрами предпериода. В знаменателе записывают число, стоящее из стольких девяток, сколько цифр в периоде, и стольких нулей, сколько цифр в предпериоде.
0,5(8) =  =
=  ;
;
в) Чтобы чистую периодическую дробь перевести в обыкновенную, необходимо в числителе записать число, образованное цифрами периода, а в знаменателе – столько 9, сколько цифр в периоде.
6,(12) = 6  = 6
= 6  .
.
0Б. Для данного множества запишите подмножества, состоящие из: а) рациональных чисел; б) иррациональных чисел; в) целых чисел.
F={  ;
;  ; 46,(3); 7,21(35);
; 46,(3); 7,21(35);  ;
;  ; 47,2(571); 2,1234567…}.
; 47,2(571); 2,1234567…}.
Решение:
а)  ; 46,(3); 7,21(35);
; 46,(3); 7,21(35);  ;
;  ; 47,2(571) – элементы множества рациональных чисел Q;
; 47,2(571) – элементы множества рациональных чисел Q;
б)  ; 2,1234567…– элементы множества иррациональных чисел I;
; 2,1234567…– элементы множества иррациональных чисел I;
в)  ;
;  – элементы множества целых чисел Z.
– элементы множества целых чисел Z.
ПОЛОЖИТЕЛЬНЫЕ РАЦИОНАЛЬНЫЕ И ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА (задания III уровня)
1А. Найдите значение выражения:  .
.
1Б. Решите уравнение, используя зависимость между результатами и компонентами арифметических действий: (2  – (1
– (1  – (х –
– (х –  ))) + 3
))) + 3  =5.
=5.
2А. Найдите значение выражения: (1,6 – 2  .
.
2Б. Решите уравнение, используя зависимость между результатами и компонентами арифметических действий: 1  + (2
+ (2  – ((
– (( 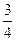 + х) + 1)) = 2
+ х) + 1)) = 2  .
.
3А. Найдите значение выражения:
(22 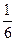 – 21
– 21  ) × 1
) × 1  + 1
+ 1  (6,3 – 3
(6,3 – 3  ).
).
3Б. Решите уравнение, используя зависимость между результатами и компонентами арифметических действий:
12 – (30 – 19 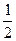 : (2
: (2 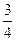 –
–  х)) ×
х)) ×  = 3.
= 3.
4А. Найдите значение выражения: 1  × 4 – (8,9 – 2,6 :
× 4 – (8,9 – 2,6 : 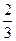 ) + 12
) + 12 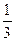 .
.
4Б. Решите уравнение, используя зависимость между результатами и компонентами арифметических действий:
(3,28 – (–1,52)) : х + (–1,3)) × (–0,04) = –0,148.
5А. Найдите значение выражения: (0,8 –  ) : 2
) : 2 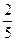 – (
– (  – 0,25) : 2
– 0,25) : 2 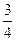 .
.
5Б. Решите уравнение, используя зависимость между результатами и компонентами арифметических действий:
3  : ((2
: ((2 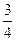 х + 4
х + 4 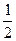 ) : 21
) : 21  ) – 1
) – 1 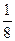 = 5
= 5  .
.
0А. Найдите значение выражения:  .
.
Решение:
1) 8,3 · 1,2 = 9,96;
2) 9,96 + 4,2 = 14,16;
3) 3  ;
;
4)  ;
;
5)  ;
;
6) 14,16 :  .
.
Ответ: 42,48.
0Б. Решите уравнение, используя зависимость между результатами и компонентами арифметических действий:
Решение:
66  : (5 + 3
: (5 + 3 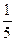 : (1
: (1  –
–  х)) – 7
х)) – 7  =
= 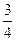 ;
;
66  : (5 + 3
: (5 + 3 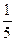 : (1
: (1  –
–  х)) =
х)) = 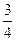 + 7
+ 7  ;
;
66  : (5 + 3
: (5 + 3 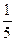 : (1
: (1  –
–  х)) = 7
х)) = 7  ;
;
5 + 3 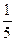 : (1
: (1  –
–  х) = 66
х) = 66  : 7
: 7  ;
;
5 + 3 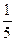 : (1
: (1  –
–  х) =
х) =  ;
;
3 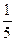 : (1
: (1  –
–  х) =
х) =  – 5;
– 5;
3 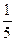 : (1
: (1  –
–  х) =
х) =  ;
;
1  –
–  х = 3
х = 3 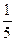 :
:  ;
;
1  –
–  х =
х =  ;
;
 х = 1
х = 1  –
–  ;
;
 х =
х =  ;
;
х =  :
:  =
=  .
.
Ответ:  .
.
ПОЛОЖИТЕЛЬНЫЕ РАЦИОНАЛЬНЫЕ И ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА (задания IV уровня)
1. Решите уравнение на основе зависимости между компонентами и результатами арифметических действий:
 =1
=1  .
.
2. Решите уравнение на основе зависимости между компонентами и результатами арифметических действий:
 =1
=1  .
.
3. Решите уравнение на основе зависимости между компонентами и результатами арифметических действий:
 =
=  .
.
4. Решите уравнение на основе зависимости между компонентами и результатами арифметических действий:
2  +
+  +1
+1  = 5.
= 5.
5. Решите уравнение на основе зависимости между компонентами и результатами арифметических действий:
 =
=  .
.
ПОЛОЖИТЕЛЬНЫЕ РАЦИОНАЛЬНЫЕ И ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА (задания V уровня)
1. Решите задачи по действиям, либо с помощью уравнения или системы уравнений:
а) На сколько процентов повысился дневной заработок рабочего, если вместо 90000 рублей он стал получать 140000 рублей?
б) На складе находится 150 ц гречневой и пшеничной круп. Сколько раз нужно взять гречневой крупы по 3,75 ц, а пшеничной по 2,625 ц, чтобы гречневой осталось в 1,45 раза меньше чем пшеничной?
2. Решите задачи по действиям, либо с помощью уравнения или системы уравнений:
а) На сколько процентов повысился почасовой заработок рабочих при переходе от 8-часового к 7-часовому рабочему дню без изменения дневного заработка?
б) Каждый их трех рабочих должен выполнить одну и ту же работу. Первый и второй вместе порученную им работу выполняют за 12 часов; второй и третий вместе за 13 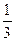 часа; первый и третий вместе за 10
часа; первый и третий вместе за 10  часа. За какое время каждый рабочий выполнит всю работу?
часа. За какое время каждый рабочий выполнит всю работу?
3. Решите задачи по действиям, либо с помощью уравнения или системы уравнений:
а) За неделю завод выпустил 588000 подшипников вместо 510000 по плану. На сколько процентов перевыполнен план?
б) Расстояние между городами 150 км. В 9 часов утра из одного города в другой выехал первый велосипедист, а в 10,2 часа того же утра навстречу ему из другого города выехал второй велосипедист, который в час проезжал на 2,5 км меньше первого велосипедиста и встретился с ним в три часа дня. С какой скоростью ехал каждый велосипедист?
4. Решите задачи по действиям, либо с помощью уравнения или системы уравнений:
а) При высыхании трава теряет 28% своей массы. Сколько было скошено травы, если получено 144 ц сена?
б) Когда один из друзей потратил  , а другой
, а другой  своих денег, то у обоих осталось поровну. Сколько денег было бы у каждого, если у первого было на 23000000
своих денег, то у обоих осталось поровну. Сколько денег было бы у каждого, если у первого было на 23000000 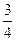 рублей больше, чем у второго?
рублей больше, чем у второго?
5. Решите задачи по действиям, либо с помощью уравнения или системы уравнений:
а) На товар стоимостью 1120000 рублей за центнер снизили цену сначала на 8%, а через некоторое время понизили цену еще на 8 %. Какова стоимость товара и какой она была бы, если бы цену понизили сразу на 16%?
б) Смешано три вида сухих ягод: 9 кг первого вида, 11 кг второго и 90 кг третьего. Сколько стоит 1 кг ягод каждого вида, если вся смесь стоит 355000 рублей и 1 кг ягод первого вида дороже 1 кг ягод второго на 3000 рублей, а 1 кг второго вида дороже 1 кг ягод третьего на 5000 рублей?
