Вычислительная томография

Слово томографияпроисходит от греческого слова «τομοσ», что означает срез, долька. Задача томографии состоит в изучении физических характеристик среды по регистрируемым аномальным эффектам, связанным с прохождением излучения через вещество. Например, поглощением с коэффициентом поглощения 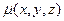или задержками пробега в связи с изменением скорости движения. Рассмотрим в качестве физической модели среды модель поглощения, описываемую как функцию 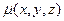пространственных координат 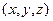. 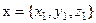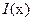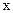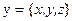Если в точке расположен источник излучения интенсивностью , излучение распространяется из в по кривой 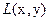, то интенсивность излучения 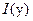в точке 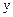в рамках линейной модели поглощения удовлетворяет дифференциальному уравнению:

,

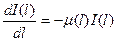(2.8)

где 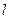- текущая точка на кривой, вдоль которой распространяется излучение. Решение этого уравнения:

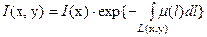представляет собой фундаментальное уравнение, связывающее модель среды – распределение коэффициента поглощения 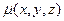и модель поля – интенсивность излучения 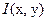в точках регистрации 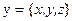. В частности:

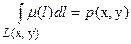, где .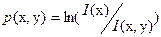

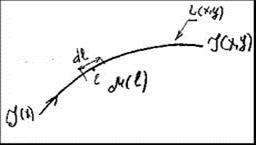
Рис.2.3 Движение вдоль луча

Если теперь множество точек 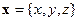, в которых возбуждается излучение пробегает некоторое многообразие 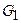, а множество детекторов 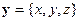излучения находится на многообразии 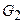, то 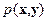- это множество интегралов коэффициента поглощения 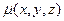вдоль линий .

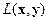В зависимости от того, как взаимно расположены источники и приемники излучения 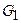и 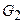, возникает та либо иная схема сканирования. В приложениях рентгеновской диагностики это параллельная или веерная схема, однако, в задачах геофизики, она чаще всего продиктована внешними, слабо контролируемыми факторами и зачастую определяется не требованиями условий разрешимости задачи реконструкции коэффициента поглощения, а обстоятельствами возможности проведения измерения. Выписанное уравнение (8) и его решение, описывают лишь часть, да и то простейшую, процессов, происходящих с излучением при прохождении его в веществе. Сам закон поглощения может быть значительно сложнее, но что самое важное, поглощение сопровождается рассеянием излучения, а это - более сложный вопрос.

Рассмотрим некоторые важные частные случаи.

Пусть ставится задача изучения объекта в сечении плоскостью X0Y и пусть линии 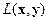прямые, не зависящие от свойств коэффициента поглощения. 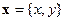, 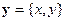.Предполагается следующая схема измерения. Детектор и источник проходят дискретно вдоль объекта, образуя параллельную систему линий 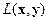. После покрытия всего объекта система источник – детектор поворачивается относительно исходного положения на угол ω, после чего процесс параллельного сканирования повторяется.

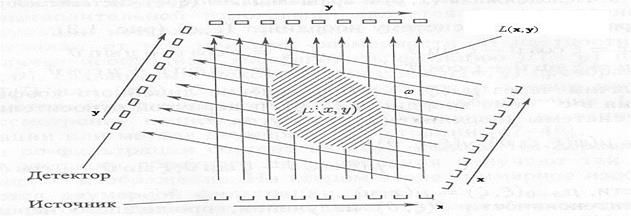
Рис.2.4 Схема установки сканирования ([1].

Так продолжается до тех пор, пока вся система источник-детектор не повернется относительно первоначального уровня на угол 180⁰. Для описания такой параллельно вращающейся системы сканирования введем вращающуюся относительно исходной систему координат:

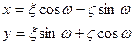
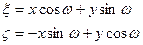
Тогда проекция p оказывается функцией новых координат:

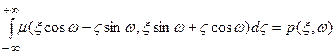(2.9)

Последнее соотношение называется преобразованием Радона. Оно было введено И.Радоном в 1917 году. Реконструкция коэффициента поглощения, таким образом, оказывается задачей обращения преобразования Радона. В силу естественных физических ограничений на условия сканирующей аппаратуры проекция задана не везде, где хотелось бы и, кроме того, с погрешностями, имеющими весьма разнообразную природу. В этой связи возникает проблема существования и единственности обратного преобразования на приближенных данных. Для того чтобы представить себе эту задачу следует найти ее решение в « теоретическом» идеализированном случае. Приведем соответствующие результаты, отсылая за подробностями к работам [1,2]

От проекции 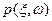перейдем к изображению 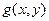по следующему правилу (обратные проекции):

.

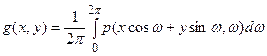Тогда связь между коэффициентом поглощения и 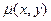и изображением 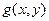установлена соотношением:

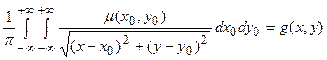(2.10)

В последнем соотношении заданной величиной – моделью физического поля служит изображение и 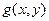, получаемое после обработки (правило обратной проекции) измеренных проекций 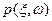. Требующая реконструкции модель поглощения 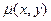связана с 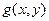уравнением (10). Уже из приведенного соотношения видно, что изображение и поглощение связаны между собой сингулярной зависимостью и процедуры вычисления будут сталкиваться с практическими проявлениями этих сингулярностей – обращением в ноль знаменателей, обращением в бесконечность или неразумно большие величины результата расчетов. Более наглядно возникающие проблемы иллюстрируются использованием другого, более конструктивного приема анализа уравнения (9), который называется методом фильтрованных обратных проекций. Этот метод основан на том, что заданные наблюдаемые проекции 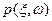подвергаются фильтрации с подбираемым ядром :

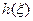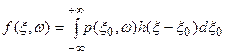, так что искомая функция поглощения 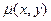вычисляется по правилу обратных проекций, аналогичному введенному выше:

.

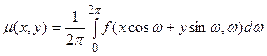Можно показать (это выполнено в работе С.А.Терещенко, которой следуем и далее), что:

.

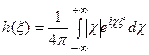Последний интеграл является расходящимся. Здесь явно проявляется проблема некорректности в вычислениях. Приближенное вычисление может быть осуществлено, например, за счет введения конечных пределов интегрирования:

.

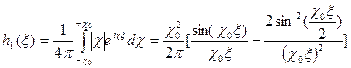Функция 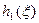отличается от 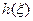и это отличие связано с отбрасыванием спектральных характеристик 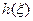, находящихся вне интервала .

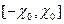Поскольку реальные измерения 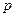заданы дискретно с шагом 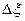: 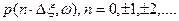, то таким же образом будет определена и функция ядра приближенного фильтра: 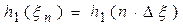.В соответствии с теоремой Котельникова непрерывная функция 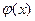, имеющая ненулевой спектр на интервале 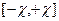, точно представима своими дискретными отсчетами:

.

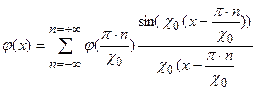Тогда отсчеты должны сниматься с дискретностью :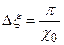

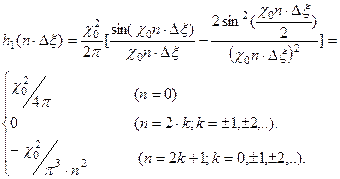Полученное выражение определяет ядро дискретного фильтра для вычисления обратных проекций и последующей реконструкции коэффициента поглощения в виде дискретного ряда Фурье. Этот фильтр называется фильтром Рамачандрана и Лакшминараянана.

Другим частным, но исключительно важным для геофизических приложений случаем, служит ситуация, при которой в уравнении

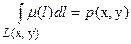
траектория 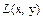распространения излучения или иначе сигнала, зависит от самого коэффициента 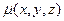. Если принять известным некоторое начальное приближение к функции 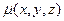- 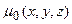, для которой известны траектории движения 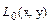, то приближенно можно записать:

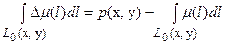
В правой части последнего равенства стоит известная функция, а определению подлежит приращение 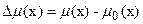. Приведенное соотношение является базовым для ультразвуковой, акустической и сейсмической томографии. При этом соответствующие параметры просто по иному называются – функции медленности, показатель преломления, временные задержки.

2.3. Сейсмические методы.

Уравнения распространения сейсмических волн – это уравнения распространения волн малых смещений относительно точки равновесия в идеально упругой изотропной среде. Они легко получаются из закона сохранения импульса, дополненного уравнениями состояния, связывающими компоненты тензора напряжений и деформаций элемента объема. Эти уравнения состояния называется законом Гука. Сами по себе они носят весьма приближенный характер, поскольку не учитывают вязкопластические, релаксационные свойства среды. Основаны на линейных идеализированных законах. Например, идеализация состоит в предположении, что на растяжение среда работает так же, как и на сжатие. Этих допущений столь много и они носят столь не очевидный характер, что получаемые уравнения распространения волн скорее носят характер наводящих соображений на описание событий реальности, эффективных законов, а вводимые скоростные параметры должны восприниматься скорее как эффективные параметры среды. На основе волновых уравнений, описывающих распространение деформаций и напряжений в среде, может быть построена лучевая теория распространения возмущений, которая характеризует «геометрию» процесса распространения волн. Лучевая теория является основой, на которой конструируются вычислительные схемы расчета времен прихода сейсмических колебаний – это наблюдаемые, по известным параметры скоростной модели среды.

Волновые уравнения.

Рассмотрим процессы, происходящие при деформации элементарного объема, для определенности куба в трехмерном пространстве.

Под действием сил элементарный объем претерпевает деформации, в результате которых точка x= 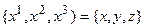переходит в точку x`. Напомним, что здесь и далее, как это принято в физической литературе, переменная индексированная латинской буквой, например j, означает компоненты этой переменной по координатным осям 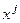. Причем пока не имеет значения используется верхний или нижний индекс. Кроме того, по дважды повторяющемуся индексу проводится суммирование по всем его значениям. Так что выражение 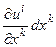следует понимать как 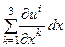. Вектор деформацииравен u=x`-x. Ребра элементарного куба до деформации были 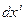. После деформации 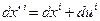. Элемент длины между точками до деформации был равен

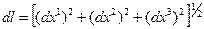
После деформации этот элемент длины стал:

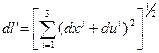
поскольку:

,

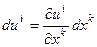то:

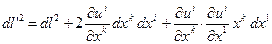
Второй член можно переписать в более симметричном виде:

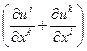
Тогда окончательно: 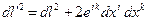, где:

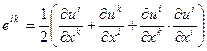
Величина 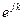называется тензором деформаций. По определению он симметричен. В том случае, когда рассматриваются малые деформации, членом 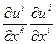можно пренебречь, поскольку он, будучи произведением малых величин, есть величина большого порядка малости. Тогда имеем:

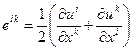
Найдем теперь величину смещения du: Пусть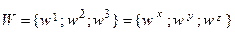

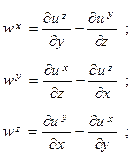
Простым вычислением проверяется справедливость такого равенства:

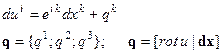
Здесь q – векторное произведение векторов 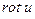и dx:

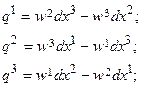
Вектор g описывает вращения, претерпеваемые при деформациях. В него не входят диагональные компоненты тензора деформаций и, следовательно, компоненты 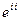описывают растяжения – сжатия.

Величина объемного сжатия-растяжения описывается с помощью параметра, называемого дилатацией Q. Дилатацияхарактеризует относительное изменение объема и численно равна:

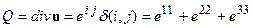
Закон Гука устанавливает связь между компонентами тензора деформации и тензора напряжений. Предполагая эту связь линейной, получим:

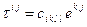
Таким образом, в рамках линейного приближения связи между деформациями и напряжениями, следует эту связь задать в виде четырехмерной (четырехиндексной) матрицы, каждый индекс которой меняется от 1 до 3. Коэффициентов этой матрицы оказывается 81. Однако, учитывая симметрию тензоров деформаций и напряжений, число этих независимых компонент снижается до 36.

Связь между компонентами тензоров деформаций и напряжений в среде без анизотропии, т.е. в среде, где свойства среды могут быть переменными по координатам, но не зависят от того, из какого направления данная координата рассматривается, описываются с помощью двух упругих констант, одна из которых ответственна за продольные деформации, другая за деформация сдвигового типа.

Используют три системы упругих параметров .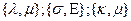

Здесь 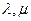- коэффициенты Ламэ, Е – модуль Юнга, 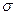- коэффициент Пуассона, 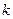– модуль всестороннего сжатия, устанавливающий связь между дилатацией и давлением:

.

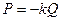Связь между этими параметрами приведена в таблице 1.

Таблица 1.

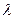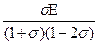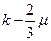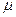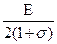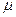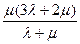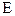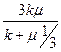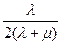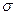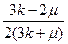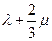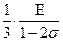		k

В рамках идеально упругой изотропной модели среды закон Гука, устанавливающий связь между компонентами тензора деформаций и напряжений, имеет следующий вид:

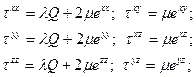(11)

Можно выразить тензор деформаций через тензор напряжений, что даст следующую форму закона Гука для нормальных компонент:

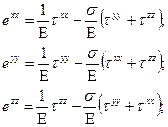(2.12)

Влияние естественных физических условий на величину упругих констант состоит в том, что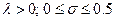

Приведенные упругие константы, в сформулированных законах «работают» как на растяжение, так и на сжатие. В реальных средах, однако, наблюдается эффект разномодульности, состоящий в том, что упругие константы, измеренные на растяжении, отличаются от соответствующих констант, измеренных на сжатии. Так, для зернистого графита модуль Юнга, измеренный при растяжении, на 20% меньше модуля упругости, измеренного при сжатии. Для чугуна модуль Юнга при сжатии на 20% выше, чем при растяжении. Для бронзы аналогичные цифры составляют 10%. Для стали – 5%.

Пусть 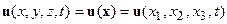- вектор смещения точки x,y,z в момент времени t. Закон сохранения импульса приводит к уравнению равновесия:

,

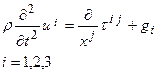(2.13)

g – объемные силы, действующие на элемент среды. Считая, что плотность 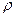не меняется со временем, и, подставляя в уравнение (13) закон Гука в форме (11), выражающий напряжения через деформации, а вместо компонент тензора деформаций – его выражения через вектор смещений, получим:

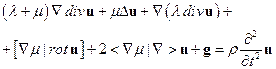(2.14)

Формула (14) представляет собой записанную в векторной форме систему из трех уравнений для трех компонент вектора смещений. Это уравнение называют волновымили уравнением поля смещений. Следует обратить внимание, во-первых, на исключительную сложность этих уравнений, а во-вторых, на то обстоятельство, что в него входят производные от параметров упругости. В случае разрыва в этих функциях и обращения производных в бесконечность это уравнение требует уточнения. Разрыв в значении параметров упругости - дело обычное в используемых геофизических моделях геологических сред. Разрывными значениями характеризуются все слоистые среды. В случае однородной среды все пространственные производные от упругих констант обращаются в ноль, и уравнение для поля смещений примет вид:

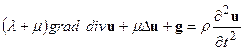(2.15)

Учитывая, что 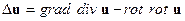, получим:

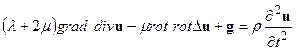(2.16)

Поле смещений, как любое поле можно разложить на потенциальную и вихревую компоненты. Тогда можно записать: 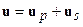, где 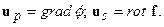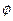и f - соответственно скалярный и векторный потенциалы.

Весь процесс смещения можно представить в виде суперпозиции двух компонент: компоненты, связанной с изменением объемов, которую называют продольными смещениями, и компоненты, связанной с вращениями, которую называют поперечными смещениямиили сдвигами. Расщепление полного поля смещения на потенциальную и вихревую части как раз и соответствует выделению продольной поперечной компонент. Покажем это.

Из условия потенциальности для 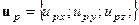следует:

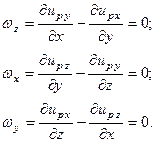
Но последнее означает, что сдвигов-вращений в компоненте 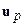нет. Деформации порождают только изменение объема вдоль распространения возмущений.

Далее для компоненты 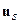имеем: 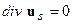. Но последнее означает, что тензор деформаций, соответствующий смещениям 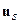, имеет нулевые диагональные элементы. Отсюда приходим к выводу о том, что смещения порожденные полем 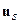, не сопровождаются изменением объема. Следовательно, это чистые сдвиги.

Поскольку 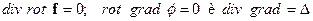, получим после подстановки представления поля смещений в виде потенциальной и вихревой части:

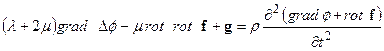(2.17)

Положим, что внешние силы отсутствуют, и колебания в среде распространяются свободно. Тогда g=0 , и уравнение (17) распадается на два:

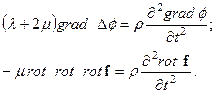
Т.к. 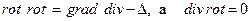, то последнее уравнение перепишется:

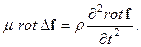
Тогда окончательно для скалярного и векторного потенциалов поля смещений получим следующие уравнения:

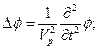(2.18)

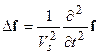(2.19)

Здесь 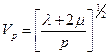– параметр, который называется скоростью распространения продольных волн. 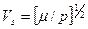называется скоростью распространения поперечных волн[1]. Уравнение (19) – это система из трех уравнений для каждой из компонент векторного потенциала f.

Уравнению вида (18) удовлетворяет и дилатация Q. Это легко показать. Для этого надо вычислить div от правой и левой части этого уравнения. Поскольку 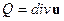, а 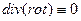,получим для дилатации уравнение

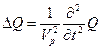. (2.20)

Таким образом, в однородной среде происходит расщепление движения на две составляющие: расширение-сжатие, распространяющееся со скоростью 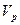, и сдвиговые деформации, распространяющиеся с меньшей скоростью 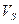. Первый тип движения называется продольными, а второй – поперечными волнами. В средах, в которых 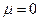, а сюда относятся жидкости, поперечные волны отсутствуют. Физически это означает отсутствие упругости в жидкости по отношению к сдвиговым деформациям. В случае неоднородных сред о существовании расщепления движений на независимые продольное и поперечное на основании анализа уравнения (16) сделать нельзя. В этой связи искусственное введение переменной скорости в уравнения (18,19) строго говоря, необоснованно и является эвристическим приемом. Однако, этот прием зачастую оправдан экспериментально. В этой связи представляется интересным вопрос о том, какого сорта неоднородности в среде следует рассматривать для того, чтобы введение переменной скорости распространения волн было теоретически обоснованным. Этот вопрос, в частности, рассматривается в приложении 4.

При получении волновых уравнений (16) закон сохранения импульса был дополнен уравнением состояния в форме исключения компонент тензора напряжений с помощью компонент тензора деформаций. Однако это же уравнение можно использовать и для обратной замены. С помощью такого приема можно получить уравнения движения не для компонент деформаций, а для компонент тензора напряжений в неоднородной среде. Причем в этом случае уравнения, описывающие волновой процесс распространения компонент тензора напряжений в среде, не будут содержать производных от параметров упругости среды.

Перепишем уравнение равновесия в форме:

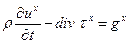(2.21-а)

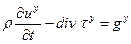(2.21-b)

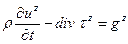(2.21-с)

Здесь:

.

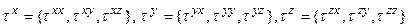Предположим, что g=0, а плотность слабо меняется при изменении пространственных координат так, что ее производные можно считать нулевыми. Тогда, дифференцируя первое уравнение последней системой по х, второе по у, третье по z, а величины:

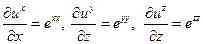
заменяя через закон Гука (12) на компоненты тензора напряжений, получим три уравнения:

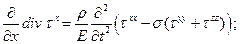(2.22-a)

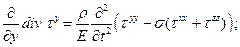(2.22-b)

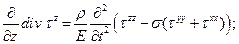(2.22-c)

Далее, дифференцируя (21-a) по у , (21-b) по х, складывая результаты и исключая с помощью закона Гука в форме (12) величину 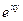, получим:

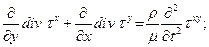(2.22-d)

Аналогичным приемом получим еще два уравнения:

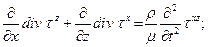(2.22-e)

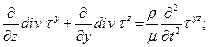(2.22-f)

Уравнения (22) представляют собой шесть уравнений относительно шести независимых компонент тензора напряжений. Эти уравнения распадаются на 2 группы. Первая группа– уравнения (22 a-c) - ответственна преимущественно за перенос диагональных компонент тензора напряжений. Вторая – (22d-f) - характеризует преимущественный перенос недиагональных компонент. В этих уравнениях, а они относятся к неоднородным средам (изотропным, идеально упругим), не содержится производных от параметров среды, а сами эти уравнения, как это легко видеть, обладают высокой степенью симметрии.

Коэффициенты, стоящие при второй производной в правой части уравнений (22 d-f) ассоциируются с величиной, обратной к квадрату скорости распространения касательных напряжений. Эта скорость в точности равна скорости распространения поперечных волн 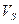. Однако, в эту систему входят и нормальные компоненты тензора напряжений. Покажем, что в предельном случае уравнения (22 a-c) дают описание распространению продольной волны напряжений с традиционной скоростью распространения продольной волны для деформаций.

Плоской волнойназывается волновой процесс, компоненты которого зависят лишь от одной пространственной координаты, вдоль которой и происходит распространение волны. Ортогонально этому направлению все параметры волнового процесса постоянны. Рассмотрим плоскую волну в неограниченной среде, распространяющуюся в направлении оси ОХ. Тогда все производные по z,y в уравнениях (22a-c) обращаются в ноль, и само уравнение приобретает вид:

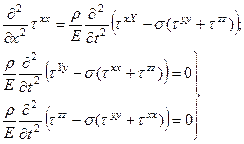(2.23)

Из последних двух уравнений, принимая во внимание естественные физические ограничения на характер поведения тензора напряжений со временем [2] , получаем:

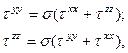
откуда:

.

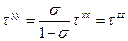Подставляя найденные выражения нормальных компонент в первое уравнение системы (23), получим:

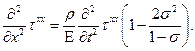
Тогда окончательно:

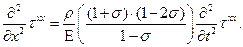
Переходя от системы упругих констант 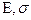к системе параметров Ламе, получаем:

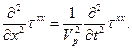
Где 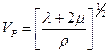- скорость распространения продольных волн.

Таким образом, приходим к выводу о распространении давления, связанного с нормальными компонентами тензора напряжений со скоростью продольной волны.

Анализ уравнений динамики напряжений позволяет нарисовать следующую качественную картину распространения волн в неоднородных средах. В неоднородной среде, как и в однородной, происходит распространение продольной волны, со скоростью V_p. Однако в отличие от однородного случая, продольная волна, в неоднородной среде порождает в каждой точке поперечные волны, которые далее распространяются со своей скоростью 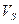, вызывая вновь вторичные продольные волны со скоростью 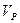. Таким образом, в неоднородной среде распространяется целый пакет возмущений, передний фронт которого связан с продольной волной, задний - с поперечной, а в области между ними присутствует смесь продольных и поперечных колебаний. Расчленение этого пакета волн на чисто продольную и чисто поперечную волну происходит в однородных средах, где нет вторичных волн.

2.3.2. Лучевая теория сейсмических волн [3,4,5].

Вернемся к уравнению равновесия:

,

.

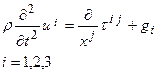Используя связь между давлением и дилатацией для гидростатических давлений ( среда представляет собой газ либо жидкость и волны - акустические): 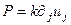получим:

.

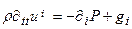Использовано обозначение: = .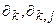

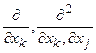В отсутствии внешних сил дифференциальное уравнение распространения акустических волн примет вид:

.

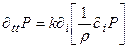Рассмотрим поле давления в ви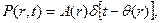де: где 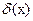- дельта Функция Дирака. Его спектр по временной координате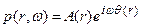

Волновые фронты — это поверхности равной фазы 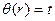- постоянные значения времени пробега 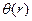. Лучи - нормали к волновым фронтам. Таким образом, q определяет геометрию лучей, А — уменьшение энергии волны. Подставляя в уравнение распространения акустических волн выражение для спектра давления, сохраняя только члены с w и w² (высокочастотное приближение), после деления на w² получим

.

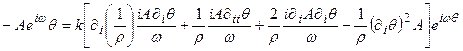Устремляя w к бесконечности, после сокращений находим:

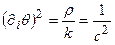(2.24)

Последнее уравнение называют уравнением Эйконала, определяющим положение волнового фронта 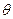. Уравнения Эйконала определяют кинематику волнового поля. Из него следует, что 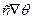— единичный вектор. Он перпендикулярен к волновому фронту и, следовательно, по определению параллелен лучу. Величина 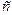имеет смысл скорости распространения возмущения. Приведенная форма уравнения Эйконала позволяет найти положение волнового фронта, однако удобнее иметь уравнение, описывающее геометрию лучей.

Пусть 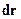— касательная к лучу с элементом длинны, обозначаемым ds. Тогда тот же единичный вектор 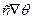можно записать как dr/ds

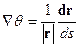С другой стороны, 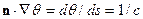и 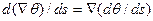,откуда получаем дифференциальное уравнение второго порядка для лучей:

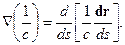(2.25)

Для численной реализации удобно преобразовать (25) в систему уравнений первого порядка. Обозначив: 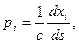получим:

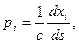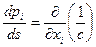(2.26)

Рассмотрим кинематику волнового поля в более общем, чем акустический, случае.

Полагая: 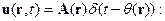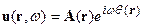, подставляя это выражение в (14), деля все на w², устремляя 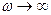, получим после сокращения членов:

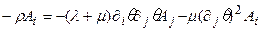
или, в векторных обозначениях:

Последнее уравнение содержит три члена, два из которых направлены вдоль А, а один — вдоль 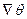. Очевидно, это уравнение можно удовлетворить только в том случае, если все ненулевые компоненты параллельны. Это будет выполнено в том случае, когда:

.

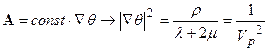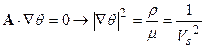(2.27)

Полученные уравнения это уравнения Эйконала, полностью аналогичны друг другу и уравнению (24). Различия состоят лишь в выражении для скорости через упругие константы. Формальное совпадение всех уравнений, отличающихся лишь выражением для скорости, гарантирует для любой упругой среды универсальность методик построения лучей.