Температурное поле импульсного точечного источника теплоты (ИТИ) в полубесконечном теле
Импульсный точечный источник теплоты, действует в течение некоторого времени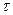 
и имеет постоянную мощность 
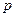в течение этого времени. Площадь воздействия источника стремится к нулю, поток энергии бесконечен. Суммарная энергия, поступающая в тело, линейно возрастает, конечна и равна: 
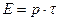. Температурное поле имеет центральную симметрию, изометрические поверхности в полубосконечном теле – полусферы с радиусом 
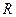. Граничную поверхность тела будем считать адиабатическойб, ось 
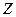направлена внутрь тела. Температурное поле ИТИ можно найти путём сложения температурных полей двух постоянно действующих точечных источников: одного реального с мощностью 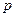, и другого фиктивного, с мощностью 
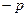(стока), начинающего дополнительно действовать в той же точке через время 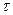. В результате имеем:
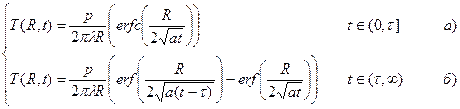(1)
Исследование температурного поля (1) несколько сложнее предыдущих случаев, так как имеется ещё один параметр – длительность импульса 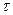. В основу анализа положим простейшую программу построения зависимости температуры от времени на фиксированном расстоянии 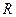от точки воздействия при фиксированной длительности импульса :
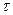1 function [t,T]=Tpiti(tau,sh,tg,p,R,m)
2 %temp pole imp ist, tau- dlit imp, sh- shag po t,tg- konec int,p- moshnost R -tek.
3 v=mview(m);
4 eval(v)
5 T0=20;
6 tu=[1:1:tg];t=tu*sh;
7 tgr=fix(tau/sh)+1;
8 TT=p/(la*2*pi*R);
9 T1=TT.*erfc(R./(2*sqrt(at*t)));
10 Tn(tgr:tg)=T1(1:(tg-tgr+1));Tn(1:tgr-1)=0;
11 T=T1-Tn+T0;
Входными параметрами программы являются: tau - длительность импульса [c], sh – шаг по времени[c], целочисленная векторная переменная tg – количество шагов по времени, 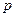- мощность источника [Вт], R – текущее расстояние до точки воздействия [см].
В строке 6 вычисляется вектор реального времени, а в строке 7 количество шагов вычисления внутри импульса. Вычисление температуры, создаваемой ПДИ (1а) осуществляется в строках 8,9. В строке 10 осуществляется сдвиг полученного массива значений температуры на величину длительности импульса, а в строке 11 происходит окончательное вычисление температуры T по (1б). Массивы t и T являются выходными параметрами подпрограммы. Приведённая подпрограмма позволяет вычислить для фиксированных значени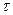й и 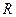. Для того что бы исследовать влияние расстояния и длительности импульса на температурное поле включим эту подпрограмму в специальные циклические подпрограммы. Подпрограмма вычисления температурного поля для набора значений радиуса :
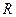1 function [t,T]=TpitiR(tau,sh,tg,p,R,m)
2 %temp pole imp ist, tau- dlit imp, sh- shag po t,tg- konec int,p- moshn, R-vek.
3 T=[];
4 n=length(R);
5 for i=1:n
6 Rt=R(i);
7 [t,Tv]=Tpiti(tau,sh,tg,p,Rt,m);
8 T=[T;Tv];
9 end
Входные и выходные параметры этой подпрограммы те же, что и в предыдущем случае, только 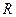может быть вектором. В строке 4 определяется длина вектора 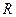, которая задаёт число циклов. В цикле, строки 5-8, происходит обращение к предыдущей подпрограмме с различными значениями 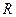, и накопление результатов в массиве 
.
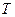Подпрограмма вычисления температурного поля для набора значений длительности импульса :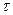
1 function [t,T]=TpitiTau(tau,sh,tg,p,R,m)
2 %temp pole imp ist, tau- dlit imp vek, sh- shag po t,tg- konec int,p- moshn vek, R-tek.
3 T=[];
4 n=length(tau);
5 k=length(p);
6 if k<n
7 p(k:n)=p(k);
8 end
9 for i=1:n
10 taut=tau(i);
11 pt=p(i);
12 [t,Tv]=Tpiti(taut,sh,tg,pt,R,m);
13 T=[T;Tv];
14 end
Эта подпрограмма аналогична предыдущей, только векторами могут быть переменные tau и p. В том случае, если размеры tau и p не совпадают в строках 5 – 8 предусмотрено их выравнивание.
Для вызова этих подпрограмм и задания начальных условий используется специальная программа:
1 function [t,T,Tm]=Tmpiti(tau,p,E,R,m)
2 %zavisimocti T ot t v tochkax R ITI: dlitelnjsti - tau, moshnoct - p;
3 v=mview(m);
4 eval(v)
5 T=[];
6 n=length(R);
7 k=length(tau);
8 if n==1 %R - chislo
9 if k==1 %tau - chislo
10 if tau==0 %tau=0
11 tmn=R^2/(6*at);sh=tmn/1000;tg=6000;tu=[1:1:tg];t=tu*sh;
12 Tv=Tpmtit(E,R,t,m); %odin MTI
13 else
14 sh=tau/1000;tg=6000;
15 if p==[] %formir p
16 p=E./tau;
17 end
18 [t,Tv]=Tpiti(tau,sh,tg,p,R,m); %odin impuls
19 end
20 else %tau -vek
21 tau=sort(tau);
22 if tau(1)==0 %tau(1)=0
23 taun(1:k-1)=tau(2:k);k=k-1;
24 tmn=min(taun);tmx=max(taun);tmxk=R^2/(6*at);
25 if tmx<tmxk
26 tmx=tmxk;
27 end
28 sh=tmn/1000;tg=fix(tmx/sh)*2;tu=[1:1:tg];t=tu*sh;
29 Tv=Tpmtit(E,R,t,m); %MTI
30 T=[T;Tv];
31 if p==[] %formir p
32 p=E./taun;
33 end
34 [t,Tv]=TpitiTau(taun,sh,tg,p,R,m);
35 else
36 tmn=min(tau);tmx=max(tau);tmxk=R^2/(6*at);
37 if tmx<tmxk
38 tmx=tmxk;
39 end
40 sh=tmn/1000;tg=fix(tmx/sh)*3;tu=[1:1:tg];t=tu*sh;
41 if p==[]
42 p=E./tau;
43 end
44 [t,Tv]=TpitiTau(tau,sh,tg,p,R,m);
45 end
46 end
47 else %R-vek;
48 if tau==0 %mgnov ist
49 [t,Tv]=Tmpt(E,R,m);
50 else
51 if p==[]
52 p=E./tau;
53 end
54 sh=tau/1000;tg=3000;
55 [t,Tv]=TpitiR(tau,sh,tg,p,R,m);
56 end
57 end
58 T=[T;Tv];
59 T=T';
60 Tm=max(T);
Данная программа позволяет проводить различные численные эксперименты, позволяющие исследовать температурные поля, создаваемые импульсными источниками тепла с различными параметрами. Входными параметрами программы являются:
- tau –длительность импульса, может содержать одно или несколько значений длительности в секундах, в том числе и нулевое;
- p-мощность (интенсивность) источника тепла в ваттах, может содержать несколько значений, но их число не должно превосходить число значений длительностей импульса, p может быть равно пустому множеству []:
- E– энергия импульса в джоулях, значение должно быть единственным и обязательно заданным, если в переменной tau задана нулевая длительность, либо если p=[];
-R – расстояние до точки воздействия в сантиметрах, может задаваться несколько не нулевых значений, но только в том случае если задано только одно значение tau, в противном случае R должно быть единственным и не равным нулю;
- m – имя материала.
Выходными параметрами являются: t – вектор моментов времени, T – вектор соответствующих значений температуры, Tm – вектор максимальных значений температуры, достигаемых при воздействии каждого импульса.
Зададим значение расстояние R=0,01см, мощность р=1000Вт и набор значений длительностей импульса 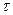=(0.0001, 0. 0002, 0. 0003, 0. 0004, 0. 0005)с. Обратимся к программе:
>> R=0.01; p=1000; m=’Cu’;
>> tau=[0.0001:0.0001:0.0005];
>> [t,T,Tm]=Tmpiti(tau,p,E,R,m);
>> plot(t,T); grid on
В результате получим:
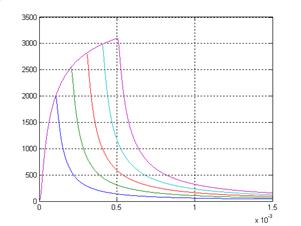
Рис. 9
На рисунке 9 показаны зависимости температуры от времени. В каждом импульсе энергия нарастает:
>> E=p*tau
E =(0.1000, 0.2000, 0.3000, 0.4000, 0.5000)Дж.
Максимальные значения температуры достигаются в конце действия каждого импульса и составляют:
Tm = 1.0e+003 *(1.9870 2.5395 2.8123 2.9818 3.1000)C0.
В программу включены также, ранее описанные подпрограммы расчёта температурных полей мгновенного точечного источника. Это позволяет сравнить зависимости температуры от времени в заданной точке при действии импульсного и мгновенного источника. Если задано p=[], то программа автоматически вычисляет значения мощности для каждого значения длительности импульса, как p=E/tau, при этом получаются импульсы равной энергии, но различной мощности. Зададим R=0.03см и E=0.01Дж и набор длительностей импульса:
>>p=[];E=0.01; m=’Cu’;
>> tau=[0,0.00002,0.0001];
>> [t,T,Tm]=Tmpiti(tau,p,E,R,m);
>> plot(t,T); grid on
Максимальные значения температуры: Tm = 1.0e+003 *(2.8661 1.7924 0.6124)С0
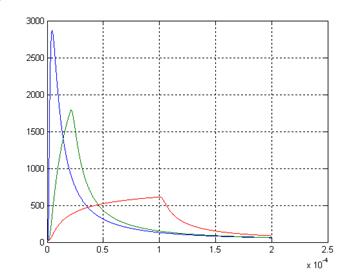
Рис. 10
Из приведённого рисунка следует, что при равной энергии, наибольшее значение температуры в точке соответствует МТИ и быстро убывает с увеличением длительности импульса. Если в тех же условиях задать малые длительности импульсов:
>> tau=[0,0.000001,0.000002]; что соответствует 0,1,2микросекундам
То на расстоянии R =0.0100см получим:
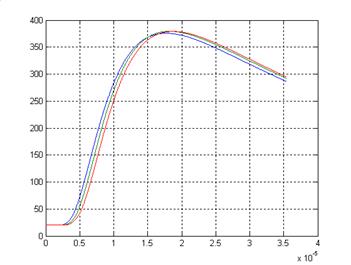
Рис. 11
Как следует из рисунка 11, температурные поля ИТИ в этом случае практически совпадают с температурным полем МТИ. Если же уменьшить расстояние в 10 раз, то разница зависимостей температуры от времени вновь станет существенной рис. 12:
>> R=0.001;
>> [t,T,Tm]=Tmpiti(tau,p,E,R,m);
>> plot(t,T); grid on
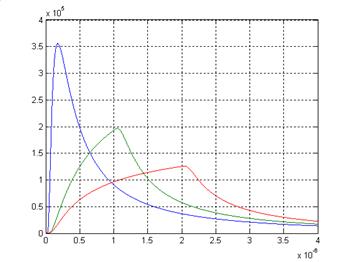
Рис. 12
Исследуем влияние расстояния на зависимости температуры от времени при фиксированных длительности импульса и мощности (энергии) импульса. Зададим:
>> E=0.001; tau=0.00003; m=’Cu’;
>>R= R=[0.002:0.002:0.008];
>> [t,T]=Tmpiti(tau,p,E,R,m);
>> plot(t,T); grid on
В результате получим:
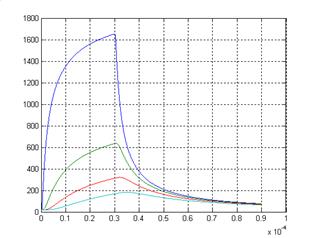
Рис. 13
Как следует из рисунка 13, максимальное значение температуры быстро убывает с расстоянием, причём максимум температуры наступает уже после окончания импульса.
Ниже приведены значения максимумов температуры, а во второй строке времена наступления этих максимумов в микросекундах.
Tm = 1.0e+003 *(1.6535 0.6379 0.3212 0.1826)
0.0301 0.0307 0.0322 0.0350
Как следует из приведённых данных это смещение не велико. Следует отметить так же, что на малых расстояниях температура достигает значений близких к предельным, а на больших, стадия выравнивания температуры начинается на участке её активного роста. Наибольший интерес представляет исследование положения изотермы плавления в зависимости от длительности и энергии импульса. Для определения положения изотермы можно воспользоваться программой нахождения решения уравнения (2) предыдущего раздела для ПДТИ, учитывая то, что максимум температуры при действии ИТИ достигается практически в конце действия импульса. Для решения этой задачи включим подпрограмму TpdiRs, описную в предыдущем разделе в циклическую программу:
function [R,Rm]=TpimpRTst(t,E,Ts,m)
%zavisimost pologenia R izotermi Ts ot vremeni-t PDI: moshnost-p,vektor vremeni-t.
v=mview(m);
eval(v)
R=[];
n=length(t);
k=length(E);
for j=1:k;
for i=1:n;
p=E(j)/t(i);
Rv(i)=TpdiRs(t(i),p,Ts,m);
end
R=[R;Rv];
end
R=R';
[Rm,f]=max(R);
stg=f*t(1)*1e6;
Rm=[Rm;stg];
Входные параметры программы:
t – вектор, содержащий набор длительностей импульса;
Е – набор энергий импульса;
Ts – температура изотермы;
m – имя материала/
Выходные параметры:
R – вектор положений изотермы с температурой Ts;
Rm – матрица, содержащая в первой строке максимумы расстояний положения изотермы Ts в сантиметрах, а во второй, соответствующие им длительности импульса в микросекундах.
Обращение к программе:
>> E=[0.001:0.002:0.007];Ts=Tpl;
>> t=[0.000001:0.000001:0.00008]; m='Cu';
>> [R,Rm]=TpimpRTst(t,E,Ts,m);
>> plot(t,R); grid on
>> Rm
Rm = 0.0029 0.0042 0.0049 0.0055
3.0000 6.0000 9.0000 12.0000
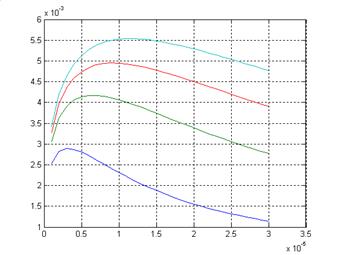
Рис. 14
Как видно из рисунка 14, каждому значению энергии соответствует некоторое оптимальное значение длительности импульса, при котором изотерма плавления продвигается вглубь материала на максимальное расстояние. Такой характер зависимости объясняется тем, что при длительностях импульса меньших оптимального значения большая часть тепла идёт на перегрев материала до температур существенно больших температуры плавления, а при больших длительностях большая часть тепла уходит на теплоотвод. Оптимальное значение длительности импульса с увеличением энергии смещается в сторону больших времён.