Аналитический метод нахождения всех минимальных ДНФ функции

Метод поиска всех максимальных интервалов заданной функции с помощью операции склеивания и сокращения.

I . Метод нахождения сокращенной ДНФ функции .

Метод будет проходить по этапам.

На начальном (нулевом) этапе рассматриваются все допустимые интервалы ранга n, т.е. СДНФ функции f . На этапе i ко всевозможным парам интервалов ранга (n-i) вида ; добавляется на интервал k ( ; ).

Предыдущая операция называется склеиванием. После чего применяется операция поглощения: если есть пара интервалов ; , то интервал удаляем. После этого переходим к очередному (i+1)–ому этапу. Если на этапе i операция склеивания не применима ни к каким интервалам, то алгоритм заканчивается и множество полученных интервалов и является в точности множеством всех максимальных допустимых интервалов.

Рассмотрим пример:

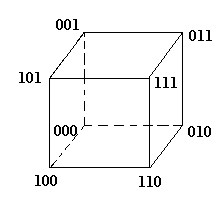
Этап 0.

; ; ; ; - поглощение.

Применяем операцию склеивания ко всевозможным интервалам.

(3-0)=3

1 и 2 , добавляем .

2 и 3, добавляем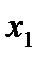

2 и 4, добавляем

3 и 5, добавляем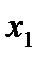

4 и 5 , добавляем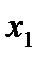

После применения операции поглощения будут удалены все интервалы ранга 3.

, , , ,

Этап 1.

Имеем интервалы ранга 3-1=2 : , , , , и применяем операцию склеивания . дадут интервал .

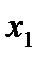После применения операции поглощения получим интервалы : ; .

Этап 2.

Ко всем интервалам ранга 2-1=1 применяем операцию склеивания . В данном случае она не применима. Алгоритм завершает работу.

Все максимальные интервалы : ,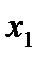

Корректность алгоритма .

Покажем, что действительно алгоритм находит все допустимые максимальные интервалы функции f.

Утверждение 1 : Все интервалы, которые возникают на этапах алгоритма являются допустимыми.

Действительно для интервалов на начальном этапе это утверждение справедливо, т.к. на начальном этапе рассматриваются допустимые интервалы максимального ранга.

Индуктивный базис .

Пусть интервал k возник в результате операции склеивания двух допустимых интервалов и . Тогда интервал k также является допустимым. Действительно, набор, на котором конъюнкция K равна 1 в компоненте, соответствующей переменной x может иметь произвольное значение 0 или 1, т. к. данная переменная не входит в множество переменных рассматриваемой конъюнкции K. Тогда, если в этой компоненте набор имеет единицу, то этот набор будет единицей конъюнкции , а если в рассматриваемой компоненте набор содержит 0, то тогда это есть единица конъюнкции . Т. е. единицы конъюнкции K принадлежат объединению единиц предыдущих двух конъюнкций. И в силу допустимости этих двух конъюнкций имеем .

Тогда справедливо , т. е. конъюнкция K – допустимый интервал.

Утверждение 2: На входе i-ого этапа интервалы ранга (n-i) в точности все допустимые интервалы такого ранга, а интервалы большого ранга есть в точности все максимальные интервалы.

Докажем данное утверждение методом индукции.

На начальном (нулевом) этапе утверждение справедливо. Интервалы ранга n на этом этапе – это все допустимые конъюнкции ранга n функции f.

Допустим утверждение справедливо для этапа i, т. е. на входе этапа i содержатся все допустимые интервалы ранга (n-i), а интервалы большего ранга есть в точности все максимальные интервалы такого ранга.

Рассмотрим (i+1) этап и докажем справедливость утверждения для этого этапа.

Во-первых, покажем, что любой допустимый интервал ранга (n-(i+1)) содержится на входе этого этапа.

Рассмотрим такой допустимый интервал k, рассмотрим переменную x, которая не входит в конъюнкцию этого интервала. Тогда интервалы и являются также допустимыми, т. к. любые единицы данных интервалов являются единицами допустимого интервала k.

Тогда в силу предположения индукции, эти два допустимых интервала ранга (n-i) содержатся на входе этапа i.

После применения операции склеивания к рассматриваемым интервалам и получается интервал k.

Во-вторых, покажем, что интервалы большего ранга, чем n-i-1 есть в точности все интервалы такого ранга.

Рассмотрим максимальный интервал ранга (n-i)k и покажем, что он будет содержатся на входе этапа i+1.

Действительно, как допустимый интервал ранга (n-i) по предположению индукции он содержался на входе этапа i. И этот интервал в силу своей максимальности не мог быть поглощенным ни одним из допустимых интервалов меньшего ранга n-i-1. А только допустимые интервалы возникают на этапах алгоритма.

Поэтому допустимый интервал k будет сохранен на этапе i и по этому будет содержатся на входе этапа (i+1).

Верно обратное утверждение, т. е. если интервал k ранга (n-i) содержится на входе i+1 этапа, то этот интервал максимальный.

Действительно, в силу доказанного данный интервал допустимый и поэтому содержится на входе этапа i, и не был поглощен на i-ом этапе. Но тогда все интервалы, которые получаются из данного интервала удалением какого-либо множителя будут недопустимыми, а поэтому данный интервал является максимальным. Поэтому доказано, что любой интервал ранга n-i является максимальным и наоборот любой максимальный ранга n-i содержится на входе i+1 этапа. Т. е. интервалы ранга n-i, есть в точности все максимальные интервалы такого ранга.

Для интервалов большего ранга, чем (n-i) утверждение о их максимальности следует из утверждения базиса индукции этапа i.

Ч.Т.Д.

Тогда из данного утверждения корректность алгоритма следует из справедливости утверждения для последнего этапа.