Построение временной функции одного из токов ветвей
Для построения временной функции выберем один из рассчитанных ранее токов. Пусть, например, это будет ток первой ветви. Его комплексное значение 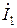 в общем виде в алгебраической форме:
в общем виде в алгебраической форме:
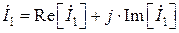 , (4.1)
, (4.1)
где: 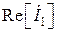 – реальная (действительная) часть комплекса тока первой ветви
– реальная (действительная) часть комплекса тока первой ветви 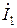 ;
; 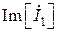 – мнимая часть комплекса тока первой ветви
– мнимая часть комплекса тока первой ветви 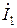 .
.
Первый ток в показательной форме комплексных чисел:
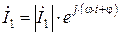 , (4.2)
, (4.2)
где: 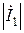 – модуль (абсолютная величина) комплекса тока первой ветви, [А], равная:
– модуль (абсолютная величина) комплекса тока первой ветви, [А], равная:
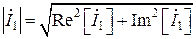 , (4.3)
, (4.3)
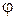 – начальная фаза гармонического колебания тока первой ветви, [рад], равная:
– начальная фаза гармонического колебания тока первой ветви, [рад], равная:
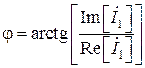 . (4.4)
. (4.4)
Записав найденный ранее комплекс тока первой ветви 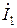 в алгебраической (4.1) и показательной (4.2) формах, можно перейти к записи этого тока во временной форме
в алгебраической (4.1) и показательной (4.2) формах, можно перейти к записи этого тока во временной форме 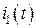 . Это можно сделать в синусоидальных проекциях (если изначально при вводе исходных данных комплексы были получены из синусоидальных проекций гармонических функций источников ЭДС):
. Это можно сделать в синусоидальных проекциях (если изначально при вводе исходных данных комплексы были получены из синусоидальных проекций гармонических функций источников ЭДС):
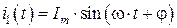 , (4.5)
, (4.5)
либо в косинусоидальных проекциях (если изначально при вводе исходных данных комплексы были получены из косинусоидальных проекций гармонических функций источников ЭДС):
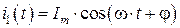 , (4.6)
, (4.6)
где: 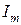 – амплитуда гармонических колебаний тока первой ветви, [А], равная модулю комплекса тока первой ветви (4.3):
– амплитуда гармонических колебаний тока первой ветви, [А], равная модулю комплекса тока первой ветви (4.3):
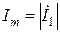 . (4.7)
. (4.7)
Круговая частота 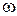 , [рад/с], определится из выражения (1.1); время
, [рад/с], определится из выражения (1.1); время 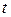 , [с], в выражении
, [с], в выражении 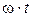 , есть текущая величина, меняя которую в пределах от 0 до
, есть текущая величина, меняя которую в пределах от 0 до 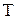 , [с], можно будет построить график временной зависимости тока первой ветви
, [с], можно будет построить график временной зависимости тока первой ветви 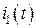 . Величина
. Величина 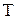 есть период колебаний, равный:
есть период колебаний, равный:
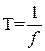 . (4.8)
. (4.8)
Величину начальной фазы 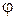 гармонических колебаний тока первой ветви
гармонических колебаний тока первой ветви 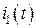 определим из выражения (4.4). После того, как определены все величины, входящие в выражение (4.5) или (4.6) гармонической функции тока первой ветви, можно построить графически эту гармоническую функцию. Для этого в декартовой системе координат по горизонтальной оси будем откладывать время
определим из выражения (4.4). После того, как определены все величины, входящие в выражение (4.5) или (4.6) гармонической функции тока первой ветви, можно построить графически эту гармоническую функцию. Для этого в декартовой системе координат по горизонтальной оси будем откладывать время 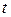 в пределах от 0 до
в пределах от 0 до 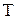 , [с], а по вертикальной оси – величину тока, полученную из выражений (4.5) или (4.6), [А].
, [с], а по вертикальной оси – величину тока, полученную из выражений (4.5) или (4.6), [А].
Например, пусть изначально источники ЭДС заданы в виде синусоидальных гармонических функций. Тогда для определения временной зависимости 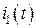 следует воспользоваться выражением (4.5). Положим, что при расчете величины
следует воспользоваться выражением (4.5). Положим, что при расчете величины 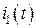 по выражениям (4.1)–(4.8) получилась следующая функция:
по выражениям (4.1)–(4.8) получилась следующая функция:
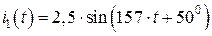 , (4.9)
, (4.9)
что соответствует исходно заданной частоте колебаний 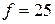 Гц, период колебаний составит
Гц, период колебаний составит 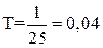 [с]. Тогда пределы построения графика
[с]. Тогда пределы построения графика  по горизонтальной оси (оси времени
по горизонтальной оси (оси времени  ) составят от 0 до 0,04 с. Величина начальной фазы колебаний в соответствии с (4.9) составляет
) составят от 0 до 0,04 с. Величина начальной фазы колебаний в соответствии с (4.9) составляет 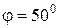 , амплитуда колебаний
, амплитуда колебаний 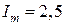 [А] (соответствует максимальному размаху колебаний тока первой ветви в области положительных, “с плюсом”, и в области отрицательных, “с минусом”, амплитуд). Тогда график временной зависимости тока первой ветви
[А] (соответствует максимальному размаху колебаний тока первой ветви в области положительных, “с плюсом”, и в области отрицательных, “с минусом”, амплитуд). Тогда график временной зависимости тока первой ветви  будет иметь вид, показанный на рис. 4.1.
будет иметь вид, показанный на рис. 4.1.
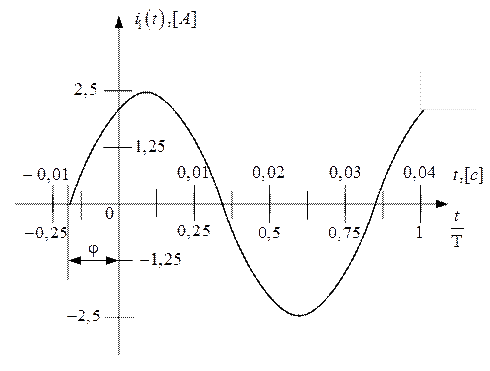
Рис. 4.1. График временной зависимости тока первой ветви  анализируемой цепи
анализируемой цепи
Для удобства на графике рис. 4.1 сверху горизонтальной оси отложены координаты времени 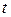 в секундах, снизу оси – координаты времени в долях периода
в секундах, снизу оси – координаты времени в долях периода 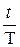 . Кроме того, на графике обозначено значение начальной фазы
. Кроме того, на графике обозначено значение начальной фазы 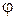 колебаний.
колебаний.
