Методические указания и задания по выполнению контрольной работы для студентов заочной формы обучения
Требования к оформлению контрольной работы
1. Контрольная работа выполняется в тетради в клетку. На обложке указать: номер зачетной книжки, вариант, дисциплину, ФИО (полностью), факультет, направление, курс, группу (см. Приложение 1).
2. Условия задач переписывать обязательно.
3. Задачи выполнять в заданном порядке.
4. Выделять результаты решения.
5. Контрольная работа должна быть сдана за 2 недели до сессии.
Числовые данные зависят от личного варианта студента (сумма цифр номера зачетной книжки), m определяется по вертикали, n определяется по горизонтали.
| n m | ||||||||||||
Найти пределы, используя эквивалентность бесконечно малых функций:
1. а) 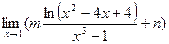 ; б)
; б) 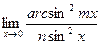 ; в)
; в) 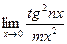 .
.
2. а) 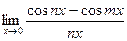 ; б)
; б) 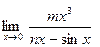 ; в)
; в) 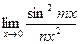 .
.
Найти пределы, используя правило Лопиталя:
3. а) 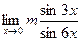 ; б)
; б) 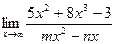 ; в)
; в) 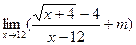 ; д)
; д) 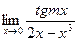 .
.
4. Задана функция 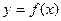 и два значения аргумента х. Требуется 1) найти пределы функции приближении к каждому из заданных значений х слева и справа; 2) установить, является ли данная функция непрерывной или разрывной для каждого из заданных значений х; 3) сделать схематический чертеж.
и два значения аргумента х. Требуется 1) найти пределы функции приближении к каждому из заданных значений х слева и справа; 2) установить, является ли данная функция непрерывной или разрывной для каждого из заданных значений х; 3) сделать схематический чертеж. 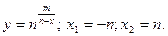
5. Задана функция 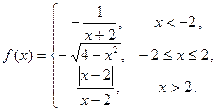
Найти все точки разрыва функции, если они существуют. Построить график функции.
6. Исследовать функцию и построить ее график: а) 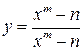 ; б)
; б) 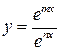 .
.
Образец оформления
Пример 1.
Исследовать функцию 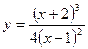 и построить ее график.
и построить ее график.
Решение.
Общая схема исследования функций:
9. Найти область определения функции.
10. Исследовать поведение функции на концах области определения. Найти точки разрыва функции и ее односторонние пределы в этих точках. Найти вертикальные асимптоты.
11. Выяснить, является функция четной, нечетной, периодической.
12. Найти точки пересечения графика функции с осями координат и интервалы знакопостоянства функции.
13. Найти наклонные асимптоты графика функции.
14. Найти точки экстремума и интервалы возрастания и убывания функции.
15. Найти точки перегиба графика функции и интервалы его выпуклости и вогнутости.
16. Построить схематический график функции, используя все полученные результаты.
1. Функция не определена, если 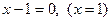
Область определения: 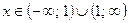
2. Т.к. 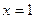 - точка разрыва функции исследуем поведение функции в этой точке слева и справа
- точка разрыва функции исследуем поведение функции в этой точке слева и справа
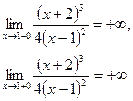
Т.к. пределы равны 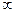 значит
значит 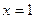 точка разрыва второго рода.
точка разрыва второго рода.
Следовательно, прямая 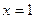 - вертикальная асимптота.
- вертикальная асимптота.
Проверим функцию на четность, нечетность. Напомним, что функция 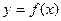 называется четной (нечетной) если выполнены два условия:
называется четной (нечетной) если выполнены два условия:
- Область определения симметрична относительно начала координат
-
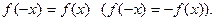
Если 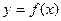 четная, то график симметричен относительно оси ординат, а для нечетной – относительно начала координат.
четная, то график симметричен относительно оси ординат, а для нечетной – относительно начала координат.
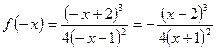
Функция не является ни четной, ни нечетной, т.е. общего вида.
Функция не является периодической
4. Найдем точки пересечения графика функции с осями координат
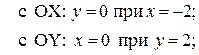
Найдем промежутки знакопостоянства функции
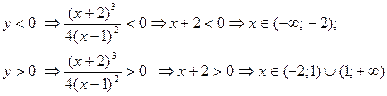
5. Найдем наклонные асимптоты 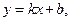 где
где
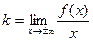
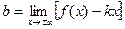
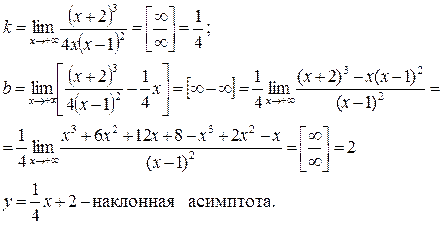
Для 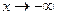 k и b вычисляются аналогично
k и b вычисляются аналогично
6. Найдем точки экстремума функции и промежутки монотонности.
Возрастание и убывание функции 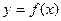 характеризуется знаком ее производной
характеризуется знаком ее производной 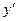 : если в некотором интервале
: если в некотором интервале 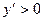 , то в этом интервале функция возрастает, а если
, то в этом интервале функция возрастает, а если 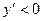 , то функция убывает в этом интервале.
, то функция убывает в этом интервале.
Функция 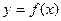 может иметь экстремум только в тех точках, которые принадлежат области определения и в которых ее производная равна нулю или не существует. Если
может иметь экстремум только в тех точках, которые принадлежат области определения и в которых ее производная равна нулю или не существует. Если 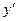 меняет знак с “+” на “-” при переходе через исследуемую точку, то эта точка максимума, если
меняет знак с “+” на “-” при переходе через исследуемую точку, то эта точка максимума, если 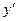 меняет знак с “-” на “+” при переходе через исследуемую точку, то эта точка является точкой минимума. Если
меняет знак с “-” на “+” при переходе через исследуемую точку, то эта точка является точкой минимума. Если 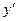 не меняет знак при переходе через точку
не меняет знак при переходе через точку 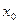 , в этой точке экстремума нет.
, в этой точке экстремума нет.
Найдем все точки из области определения функции 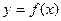 , в которых производная
, в которых производная 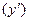 обращается в ноль или не существует.
обращается в ноль или не существует.
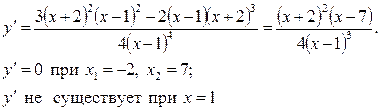
Составим таблицу
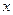 | 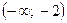 | -2 | 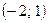 | 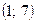 | 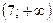 | ||
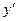 | + | + | не существует | - | + | ||
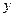 |  |  | не существует |   | 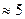 |  | |
| возрастает | возрастает | убывает | min | возрастает |
Функция возрастает на интервалах 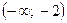 ,
, 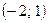 ,
, 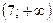 и убывает на интервале
и убывает на интервале 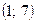 . Точка
. Точка  есть точка минимума
есть точка минимума 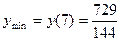
7. Найдем точки перегиба и промежутки выпуклости и вогнутости функции
Напомним, что график функции 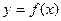 называется выпуклым на интервале
называется выпуклым на интервале 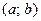 , если в каждой точке этого интервала график лежит ниже любой своей касательной. График функции
, если в каждой точке этого интервала график лежит ниже любой своей касательной. График функции 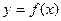 называется вогнутым на интервале
называется вогнутым на интервале 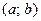 , если в каждой точке этого интервала график лежит выше любой своей касательной.
, если в каждой точке этого интервала график лежит выше любой своей касательной.
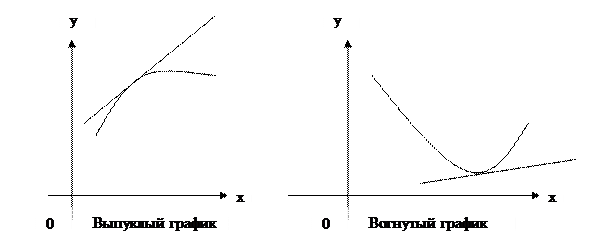
Точки, в которых функция меняет выпуклость на вогнутость или наоборот, называются точками перегиба.
Перегиб возможен в точках, в которых 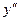 равна нулю или не существует. Если
равна нулю или не существует. Если 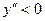 на интервале
на интервале 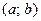 , то график функции является выпуклым
, то график функции является выпуклым 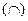 на этом интервале, если же
на этом интервале, если же 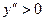 , то на интервале
, то на интервале 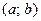 график вогнутый
график вогнутый 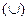 .
.
Найдем точки перегиба 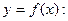
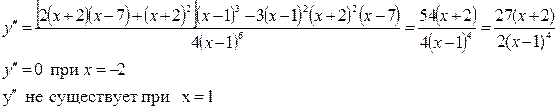
Составим таблицу
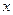 | 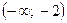 | -2 | 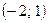 | 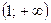 | |
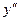 | - | + | не существует | + | |
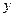 | 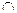 | 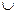 | не существует | 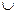 |
Точка 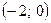 - точка перегиба.
- точка перегиба.
Дополнительные точки:
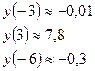
8. Построим график функции, используя результаты исследования.
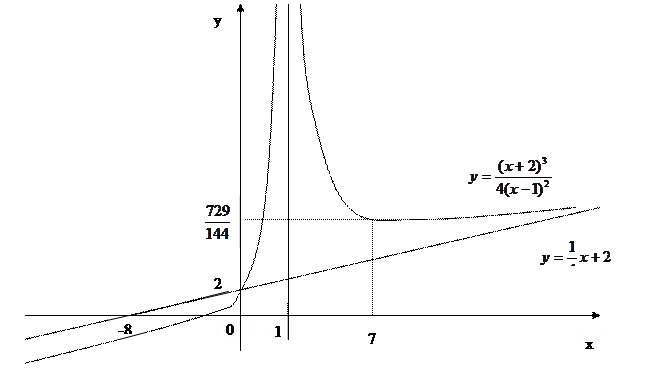
Замечание:При построении графика масштабы по оси OX и OY могут не совпадать.
ПРИЛОЖЕНИЕ 1
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
НЕФТЕКАМСКИЙ ФИЛИАЛ
ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Заочное отделение
