Пример выполнения работы. Вычислить интеграл:
Вычислить интеграл: 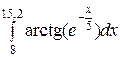 .
.
1. Разобьем отрезок интегрирования 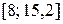 на 8 частей. В результате получим, что шаг интегрирования
на 8 частей. В результате получим, что шаг интегрирования 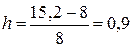 , а точки разбиения:
, а точки разбиения:
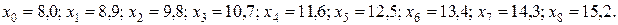
Вычислим значения функции 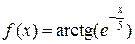 и конечные разности
и конечные разности 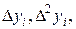
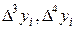 по формулам (3.17) в этих точках. Результаты занесем в табл. 3.2.
по формулам (3.17) в этих точках. Результаты занесем в табл. 3.2.
Таблица 3.2
Результаты вычислений 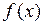 и конечных разностей
и конечных разностей
| I | 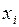 | 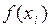 | 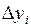 | 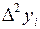 | 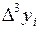 | 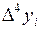 |
| 8.0 | 0,199218 | – 0,032152 | 0,005024 | – 0,000718 | 0,000073 | |
| 8.9 | 0,167066 | – 0,027128 | 0,004306 | – 0,000641 | 0,000075 | |
| 9,8 | 0,139938 | – 0,022822 | 0,003665 | – 0,000566 | 0,000079 | |
| 10,7 | 0,117116 | – 0,019157 | 0,003099 | – 0,000487 | 0,000069 | |
| 11,6 | 0,097959 | – 0,016058 | 0,002613 | – 0,000418 | 0,000065 | |
| 12,5 | 0,081901 | – 0,013445 | 0,002195 | – 0,000353 | ||
| 13,4 | 0,068456 | – 0,011250 | 0,001842 | |||
| 14,3 | 0,057206 | – 0,009408 | ||||
| 15,2 | 0,047798 |
2. По формуле трапеций (3.4) находим
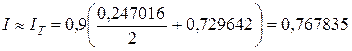
3. Аналогично проводим вычисления по формуле Симпсона (3.9):
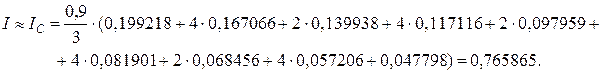
4. Оценим погрешности вычислений. Погрешность округления
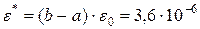
(значения функции 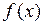 вычислены с ошибкой
вычислены с ошибкой 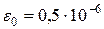 , так как округления производились в шестом знаке после запятой). Оценку погрешностей методов проводим по формулам (3.21) и (3.22). Так как
, так как округления производились в шестом знаке после запятой). Оценку погрешностей методов проводим по формулам (3.21) и (3.22). Так как 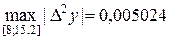 , то для метода трапеций
, то для метода трапеций
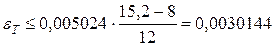
и полная погрешность 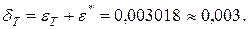 Следовательно
Следовательно 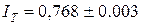 . Соответственно для метода Симпсона имеем
. Соответственно для метода Симпсона имеем
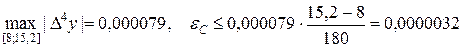
и 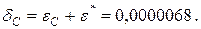 Поэтому
Поэтому 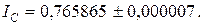 Таким образом, метод Симпсона дает значительно более точный результат, чем метод трапеций.
Таким образом, метод Симпсона дает значительно более точный результат, чем метод трапеций.
5. Продолжаем выполнение работы в компьютерном классе. Запускаем программу Mathcad. Открываем файл Lab3.mcd. Вводим функцию
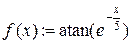 ,
,
а также нижний и верхний предел интегрирования
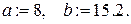
Программа автоматически строит график подынтегральной функции 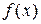 на отрезке
на отрезке 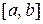 (рис. 3.7).
(рис. 3.7).
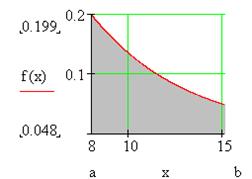
Рис. 3.7. График подынтегральной функции
Таким образом, из геометрического смысла определенного интеграла следует, что необходимо вычислить площадь криволинейной трапеции (серая область на рис. 3.7).
Программа автоматически вычисляет интеграл с точностью до 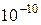 :
:
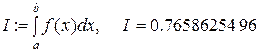
6. Выписываем полученное на компьютере решение
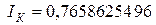
и вычисляем абсолютные погрешности, с какими найдены с помощью МК значения интеграла по методу трапеций и Симпсона:
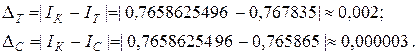
7. Используя формулы (3.23), программа в конце пункта «Метод левых прямоугольников» вычислит число точек разбиения отрезка интегрирования 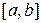 , обеспечивающее точность
, обеспечивающее точность 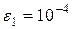 методов левых и правых прямоугольников. Получим
методов левых и правых прямоугольников. Получим
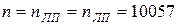 .
.
Подставляя 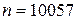 в начало пункта «Метод правых прямоугольников» программы, выписываем получившееся решение
в начало пункта «Метод правых прямоугольников» программы, выписываем получившееся решение
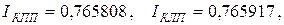
с абсолютными погрешностями
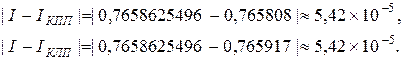
8. Используя формулу (3.24), программа в конце пункта «Метод средних прямоугольников» вычисляет число точек разбиения отрезка интегрирования 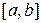 , обеспечивающее точность
, обеспечивающее точность 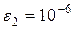 метода средних прямоугольников. Получим
метода средних прямоугольников. Получим
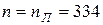 .
.
Подставляя 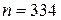 в начало пункта «Метод средних прямоугольников» программы, выписываем получившееся решение
в начало пункта «Метод средних прямоугольников» программы, выписываем получившееся решение
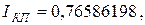
с абсолютной погрешностью
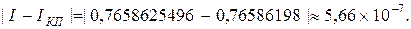
9. Используя формулу (3.25), программа в конце пункта «Метод трапеций» вычисляет число точек разбиения отрезка интегрирования 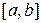 , обеспечивающее точность
, обеспечивающее точность 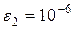 метода трапеций. Получим
метода трапеций. Получим
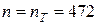 .
.
Подставляя 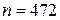 в начало пункта «Метод трапеций» программы, выписываем получившееся решение
в начало пункта «Метод трапеций» программы, выписываем получившееся решение
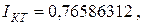
с абсолютной погрешностью
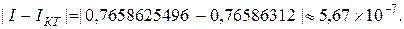
10. Используя формулу (3.26), программа в конце пункта «Метод Симпсона» вычисляет число точек разбиения отрезка интегрирования 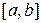 , обеспечивающее точность
, обеспечивающее точность 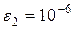 метода Симпсона. Получим
метода Симпсона. Получим 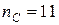 . Следовательно, так как n должно быть четным, подставляем
. Следовательно, так как n должно быть четным, подставляем 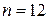 в начало пункта «Метод Симпсона» программы. Выписываем получившееся решение
в начало пункта «Метод Симпсона» программы. Выписываем получившееся решение
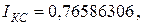
с абсолютной погрешностью
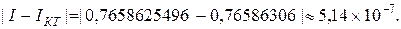
11. Все расчеты оформляются в виде отчета по лабораторной работе.
Вопросы для самоконтроля
1. Дайте определение определенного интеграла.
2. Дайте определение неопределенного интеграла.
3. Что такое первообразная для функции?
4. Приведите формулу Ньютона-Лейбница.
5. В каких случаях целесообразно использовать формулы численного интегрирования?
6. Используя геометрическую интерпретацию, выведите формулы левых и правых прямоугольников.
7. Приведите оценку погрешности формул левых и правых прямоугольников.
8. Выведите формулу средних прямоугольников.
9. Приведите оценку погрешности формулы средних прямоугольников.
10. Выведите формулу трапеций.
11. Приведите оценку погрешности формулы трапеций.
12. Выведите формулу Симпсона.
13. Приведите оценку погрешности формулы Симпсона.
14. Получите формулу выбора начального шага в формуле трапеций.
15. Получите формулу выбора начального шага в формуле Симпсона.
16. В чем состоит правило Рунге оценки погрешностей? Получите оценки погрешностей формул трапеций и Симпсона по правилу Рунге.
17. Как находится полная погрешность вычисления определенного интеграла?
