Итерационные методы построения решений на экстремальных классах
Для решения уравнения (72) построим итерационный процесс:
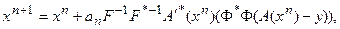 (5.73)
(5.73)
где 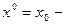 заданное нулевое приближение,
заданное нулевое приближение, 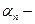 последовательность чисел (называемых параметрами релаксации), обеспечивающая сходимость (73). Предположим, что нам удалось выбрать последовательность
последовательность чисел (называемых параметрами релаксации), обеспечивающая сходимость (73). Предположим, что нам удалось выбрать последовательность 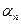 так, что последовательность
так, что последовательность 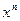 сходится. Тогда, если для всех
сходится. Тогда, если для всех 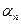 :
: 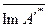
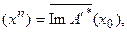 что включает в себя и введенное ранее предположение (51), то
что включает в себя и введенное ранее предположение (51), то
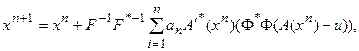
и, следовательно, для предельного элемента имеем:
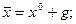
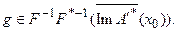
Последнее означает, что определенный элемент 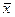 принадлежит экстремальному классу (46) и, тем самым, обладает требуемыми свойствами оптимальности. С другой стороны, этот же элемент минимизирует невязку
принадлежит экстремальному классу (46) и, тем самым, обладает требуемыми свойствами оптимальности. С другой стороны, этот же элемент минимизирует невязку
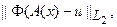 (5.74)
(5.74)
и, следовательно, процесс (73), при условии его сходимости, решает задачу оптимального подбора относительно априори заданного критерия и минимизирующего невязку по полю в смысле (74).
Займемся теперь выбором последовательности 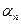 . Для этого поступим способом, аналогичным приведенному в предыдущем разделе – способом минимальных невязок. Потребуем, чтобы последовательность
. Для этого поступим способом, аналогичным приведенному в предыдущем разделе – способом минимальных невязок. Потребуем, чтобы последовательность 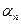 выбиралась так, что для соответствующей по (73) последовательности
выбиралась так, что для соответствующей по (73) последовательности 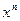 обеспечивалась максимальная скорость убывания величины:
обеспечивалась максимальная скорость убывания величины:
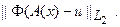
Обозначим: 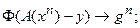
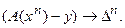
Поскольку:
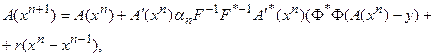
где 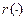 - величина второго порядка малости (относительно
- величина второго порядка малости (относительно 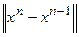 ), то:
), то:
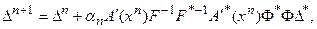
и
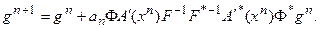
Отсюда:
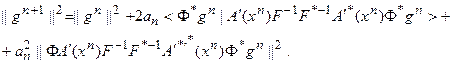
Тогда:
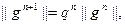
где: 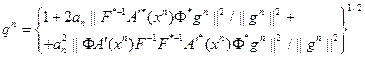 . (5.75)
. (5.75)
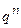 – есть функция
– есть функция  и, для того, чтобы обеспечить максимальную скорость убывания
и, для того, чтобы обеспечить максимальную скорость убывания 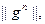 необходимо минимизировать
необходимо минимизировать 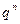 по
по  . Продифференцируем (75) по
. Продифференцируем (75) по 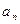 , и приравняем результат нулю. Получим:
, и приравняем результат нулю. Получим:
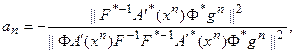 (5.76)
(5.76)
что можно переписать также и в эквивалентной форме:
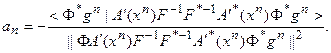
Необходимо убедиться, что величина 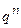 при таком выборе
при таком выборе 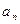 лежит в интервале (0,1). Этим обеспечивается монотонность убывания невязки. Подставив (76) в (75), получим:
лежит в интервале (0,1). Этим обеспечивается монотонность убывания невязки. Подставив (76) в (75), получим:
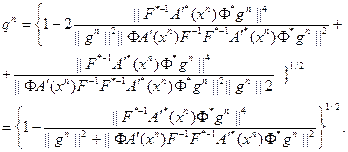 (5.77)
(5.77)
Числитель в (77) перепишем:
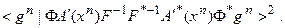
Неравенство Шварца гласит:
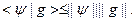
Тогда:
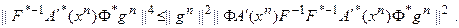
Следовательно, величина 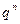 вещественна и имеет значения из интервала (0,1). Этим обеспечивается монотонное убывание невязки, определенной соотношением (74), при вычислении параметра релаксации по формуле (76).
вещественна и имеет значения из интервала (0,1). Этим обеспечивается монотонное убывание невязки, определенной соотношением (74), при вычислении параметра релаксации по формуле (76).
Если при некотором 
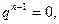 то невязка
то невязка 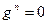 и, следовательно, итерационный процесс сошёлся, и для выделенного элемента
и, следовательно, итерационный процесс сошёлся, и для выделенного элемента 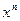 имеем
имеем 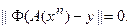 Отсюда следует
Отсюда следует 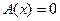 (оператор Ф взаимно - однозначен на
(оператор Ф взаимно - однозначен на 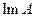 ). Рассмотрим другой предельный случай. Предположим, что невязка прекратила убывать. Следовательно,
). Рассмотрим другой предельный случай. Предположим, что невязка прекратила убывать. Следовательно, 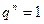 и:
и:
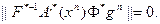
Поскольку 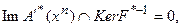 то, следовательно,
то, следовательно, 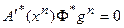 и, либо
и, либо 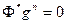 , либо
, либо 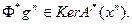 В приложениях оператор Ф имеет нулевое ядро. Например, в качестве Ф может служить операция умножения на некоторую неотрицательную весовую функцию; либо
В приложениях оператор Ф имеет нулевое ядро. Например, в качестве Ф может служить операция умножения на некоторую неотрицательную весовую функцию; либо 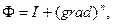 где
где 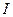 - единичный оператор. невязку, но и производные от невязки до фиксированного порядка.
- единичный оператор. невязку, но и производные от невязки до фиксированного порядка.
Считая, что 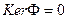 и
и 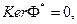 имеем, в силу теоремы о ядре
имеем, в силу теоремы о ядре
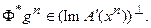
Иными словами, используемая трансформация достигнутой невязки 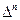 ортогональна всему множеству значений оператора
ортогональна всему множеству значений оператора 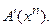 Если, например,
Если, например, 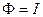 , то такая ситуация может свидетельствовать о том, что компонента
, то такая ситуация может свидетельствовать о том, что компонента 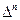 не укладывается в рамки принятых модельных представлений о среде и не может быть учтена без пересмотра этих представлений и введения ее новых компонентов.
не укладывается в рамки принятых модельных представлений о среде и не может быть учтена без пересмотра этих представлений и введения ее новых компонентов.
Для того, чтобы решение, найденное как предел итерационного процесса (73), обладало свойствами оптимальности, постулированными постановкой обратной задачи (65), необходимо, чтобы 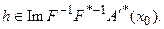 В итерационном процессе, кроме того, предполагается
В итерационном процессе, кроме того, предполагается 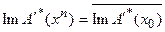 для всех
для всех 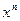 из некоторой окрестности
из некоторой окрестности 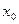 . Тогда, в силу теоремы о ядре, имеем:
. Тогда, в силу теоремы о ядре, имеем: 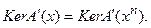 Такое условие в некоторых задачах, обладающих особо большой эквивалентностью, представляется чрезмерно ограничительным. Для того чтобы обеспечить выполнение условия
Такое условие в некоторых задачах, обладающих особо большой эквивалентностью, представляется чрезмерно ограничительным. Для того чтобы обеспечить выполнение условия 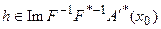 и, тем самым, требуемые свойства оптимальности решения, можно пользоваться модифицированным итерационным процессом:
и, тем самым, требуемые свойства оптимальности решения, можно пользоваться модифицированным итерационным процессом:
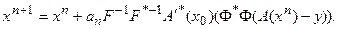 (5.78)
(5.78)
Его отличие от основного состоит в том, что на каждом шаге итерационного процесса производная оператора рассматривается в одной и той же точке – принятом нулевом приближении. Параметр релаксации при этом вычисляется по модифицированному соотношению:
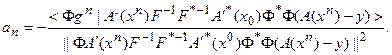 (5.79)
(5.79)
Последняя формула получена заменой 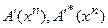 в (76) на
в (76) на 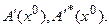 Все дальнейшие рассмотрения повторяются дословно. Сходимость модифицированного процесса (78) будет происходить до тех пор, пока:
Все дальнейшие рассмотрения повторяются дословно. Сходимость модифицированного процесса (78) будет происходить до тех пор, пока:
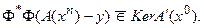
В противном случае процесс прекращает сходиться. Выполнения условия
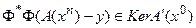 ,
,
также можно трактовать как несоответствие оставшейся невязки принятым представлениям о среде.
Описанный итерационный процесс приемлем и для решения линейных задач на экстремальных классах, в частности, решения задачи:
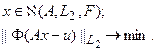
В этом случае он имеет вид:
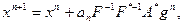 (5.80)
(5.80)
где:
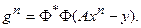
Как видно, соотношение (80) полностью повторяет (54). Обобщение состоит в ведении оператора 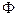 , контролирующего особые свойства невязки. Прекращение сходимости процесса означает:
, контролирующего особые свойства невязки. Прекращение сходимости процесса означает:
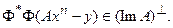
Реально, итерационные процессы (73, 78) продолжаются ограниченное число шагов N, в результате чего достигается невязка по полю 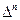 . Далее процесс прекращается. Для выбора числа этих шагов можно пользоваться принципом обобщенной невязки, уже описанным выше. Вкратце его применение сводится к следующему.
. Далее процесс прекращается. Для выбора числа этих шагов можно пользоваться принципом обобщенной невязки, уже описанным выше. Вкратце его применение сводится к следующему.
Если оператор А задан с ошибкой так, что реально используется оператор 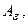 и его уклонение от точного оценивается величиной:
и его уклонение от точного оценивается величиной: 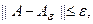
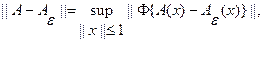
И, кроме того наблюдаемая  также задана с ошибкой, и:
также задана с ошибкой, и:
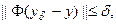
то в качестве критерия остановки итерационного процесса может служить:
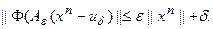
Действительно, с точностью до членов второго порядка 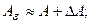
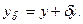
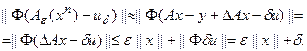
Обратим внимание на следующее, важное с вычислительной точки зрения, обстоятельство. Формула (76) для расчета параметра релаксации 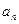 кажется громоздкой. Однако в процессе вычислений по итерациям (73) все необходимые компоненты, входящие в (76), уже вычислены, и количество дополнительных расчетов для нахождения параметра релаксации
кажется громоздкой. Однако в процессе вычислений по итерациям (73) все необходимые компоненты, входящие в (76), уже вычислены, и количество дополнительных расчетов для нахождения параметра релаксации 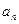 оказывается невелико.
оказывается невелико.
Описанная итерационная схема не является обязательной для критериального подхода. Главным является то, что получаемое решение должно принадлежать множеству с представлением (66), либо, если не пользоваться линеаризацией для формирования принципов оптимальности – множеству с представлением (59). Какая бы технология нахождения конкретного решения уравнения  не использовалась, если она приводит к решению, представленному в виде (59) либо (67) при
не использовалась, если она приводит к решению, представленному в виде (59) либо (67) при 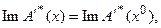 то, тем самым, решена и задача (58). В некоторых случаях целесообразен эвристический подбор параметра релаксации на основании анализа динамики невязки. Эта схема основана на экстраполяции значения параметра релаксации на основе графика зависимости невязки от величины параметра релаксации, полученного на предыдущих шагах итерационного процесса.
то, тем самым, решена и задача (58). В некоторых случаях целесообразен эвристический подбор параметра релаксации на основании анализа динамики невязки. Эта схема основана на экстраполяции значения параметра релаксации на основе графика зависимости невязки от величины параметра релаксации, полученного на предыдущих шагах итерационного процесса.
Типичным примером другого типа алгоритмов для решения нелинейных уравнений является метод Маккварта[1]. Его сущность состоит в следующем.
Для заданного нулевого приближения 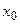 , уравнение
, уравнение  заменяется на:
заменяется на:
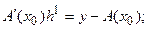 (5.81)
(5.81)
где 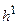 - поправка к вектору
- поправка к вектору  и
и 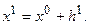 Для согласования размерностей правой и левой частей уравнения (81) последнее умножается слева на сопряженную к
Для согласования размерностей правой и левой частей уравнения (81) последнее умножается слева на сопряженную к 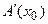 матрицу
матрицу 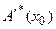 :
:
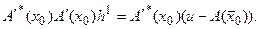 (5.82)
(5.82)
Поскольку матрица 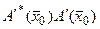 может оказаться плохо обусловленной или даже выраженной, то вводится регуляризующий член, и уравнение (82) заменяется на:
может оказаться плохо обусловленной или даже выраженной, то вводится регуляризующий член, и уравнение (82) заменяется на:
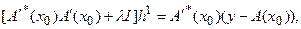 (5.83)
(5.83)
где 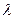 - некоторый числовой параметр и
- некоторый числовой параметр и 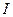 - единичная матрица. Уравнение (83) – система линейных уравнений. Решая ее относительно
- единичная матрица. Уравнение (83) – система линейных уравнений. Решая ее относительно 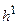 , получим новое, исправленное значение
, получим новое, исправленное значение 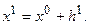 Повторяя процесс далее, получим:
Повторяя процесс далее, получим: 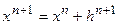 и для искомого решения:
и для искомого решения:
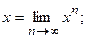
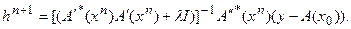 (5.84)
(5.84)
При 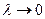 метод Маккварта асимптотически редуцируется к методу наименьших квадратов. При больших
метод Маккварта асимптотически редуцируется к методу наименьших квадратов. При больших 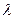 метод Маккварта аналогичен методу наискорейшего спуска. Выбор конкретного значения
метод Маккварта аналогичен методу наискорейшего спуска. Выбор конкретного значения 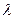 здесь представляет некоторые трудности и, видимо, некоторой универсальной рекомендации по этому вопросу дать нельзя. Для решения частных обратных задач, например, обратных задач магнитотеллурического зондирования [2], разработаны методические рекомендации по выбору параметра
здесь представляет некоторые трудности и, видимо, некоторой универсальной рекомендации по этому вопросу дать нельзя. Для решения частных обратных задач, например, обратных задач магнитотеллурического зондирования [2], разработаны методические рекомендации по выбору параметра 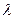 , который меняется пошагово, в зависимости от поведения невязки. Выбору параметра
, который меняется пошагово, в зависимости от поведения невязки. Выбору параметра 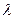 можно дать трактовку в рамках идеологии теории регуляризации, поскольку добавочное слагаемое – член
можно дать трактовку в рамках идеологии теории регуляризации, поскольку добавочное слагаемое – член 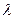 I, есть ни что иное, как регуляризующее слагаемое. Однако нас в настоящее время интересует другой аспект вопроса. Перепишем систему (84) следующим образом:
I, есть ни что иное, как регуляризующее слагаемое. Однако нас в настоящее время интересует другой аспект вопроса. Перепишем систему (84) следующим образом:
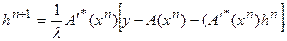 .
.
Последнее означает, что 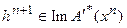 и, следовательно,
и, следовательно, 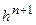 есть решение задачи:
есть решение задачи:
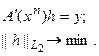
Таким образом, решение Маккварта по своим экстремальным свойствам соответствует наименее уклоняющемуся от нуля в смысле 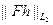 при
при 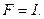 Иными словами принадлежит почти идеальному экстремальному классу
Иными словами принадлежит почти идеальному экстремальному классу 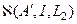 Теперь нетрудно модифицировать схему Маккварта так, чтобы получаемое решение обладало теми же экстремальными свойствами, что и в схеме (73) при произвольном операторе
Теперь нетрудно модифицировать схему Маккварта так, чтобы получаемое решение обладало теми же экстремальными свойствами, что и в схеме (73) при произвольном операторе 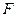 (принадлежало экстремальному классу
(принадлежало экстремальному классу 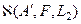 ):
):
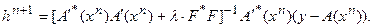 (5.85)
(5.85)
Легко заметить, что: 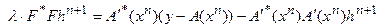
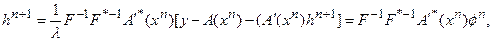
где 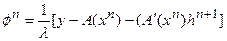 .
.
Требуемое представление для 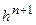 достигнуто.
достигнуто.
Метод построения решения обратной задачи, основанный на использовании модифицированного метода Маккварта (85), требует на каждом шаге решения системы линейных уравнений. В том случае, когда это осуществимо (относительно небольшое число искомых параметров), и при правильном выборе 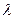 , этот метод оказывается преимущественным по точности решения (относительно невязки
, этот метод оказывается преимущественным по точности решения (относительно невязки 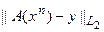 в сравнении с итерационным процессом (73)). Однако необходимость решения системы линейных уравнений оказывается весьма серьёзным препятствием при поиске много размерных параметров. Так, например, при решении обратной задачи гравиразведки в классе плотных границ для профиля средней величины (60 км при масштабе съёмки 1:50000) и средней сложности (3 искомых контакта) такой подход требовал бы решения системы из 620 уравнений. Это трудоемкая задача, а необходимость её многократного решения затрудняет ситуацию. В конечном итоге оказывается более выгодным осуществить дополнительные итерации в (73), чем повышать точность за счет решения больших систем уравнений. Описанная ситуация характерна для многих сегодняшних задач, поскольку желание повысить итерационные возможности геофизического метода приводит к увеличению числа искомых параметров.
в сравнении с итерационным процессом (73)). Однако необходимость решения системы линейных уравнений оказывается весьма серьёзным препятствием при поиске много размерных параметров. Так, например, при решении обратной задачи гравиразведки в классе плотных границ для профиля средней величины (60 км при масштабе съёмки 1:50000) и средней сложности (3 искомых контакта) такой подход требовал бы решения системы из 620 уравнений. Это трудоемкая задача, а необходимость её многократного решения затрудняет ситуацию. В конечном итоге оказывается более выгодным осуществить дополнительные итерации в (73), чем повышать точность за счет решения больших систем уравнений. Описанная ситуация характерна для многих сегодняшних задач, поскольку желание повысить итерационные возможности геофизического метода приводит к увеличению числа искомых параметров.
5.7. Составные критерии оптимальности и обратные задачи комплексной интерпретации.
Чем шире класс эквивалентности  , тем более решение задачи
, тем более решение задачи  в рамках критериального подхода зависит от принятого критерия оптимальности, или, иначе, от параметров
в рамках критериального подхода зависит от принятого критерия оптимальности, или, иначе, от параметров 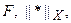 входящих в его выражение:
входящих в его выражение:
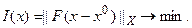
Сам по себе этот факт – объективное обстоятельство, и даже может рассматриваться как явление положительное, поскольку позволяет управлять свойствами получаемого решения. Последнее верно, если имеется объективный способ анализа получаемых решений из экстремальных классов 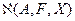 . Однако факт такого влияния имеет и серьёзные отрицательные стороны. Дело в том, что при выводе выражений для экстремальных классов
. Однако факт такого влияния имеет и серьёзные отрицательные стороны. Дело в том, что при выводе выражений для экстремальных классов 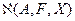 , на оператор
, на оператор 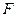 , норму пространства
, норму пространства  накладывались чисто математические ограничения. Это ограничивало класс используемых критериев оптимальности. Это обстоятельство, а также влияние неизбежного субъективизма и погрешностей в формировании оператора
накладывались чисто математические ограничения. Это ограничивало класс используемых критериев оптимальности. Это обстоятельство, а также влияние неизбежного субъективизма и погрешностей в формировании оператора 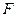 , приводит к тому, что вместо необходимого вида
, приводит к тому, что вместо необходимого вида 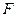 (который может быть и неизвестен) применяется другой –
(который может быть и неизвестен) применяется другой – 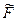 , возможно, близкий к
, возможно, близкий к 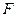 , но не разный ему тождественно. Различие между решениями из
, но не разный ему тождественно. Различие между решениями из 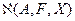 и
и 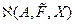 будет тем более, чем шире класс
будет тем более, чем шире класс 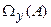 . Поэтому, если имеется дополнительная информация, позволяющая сузить
. Поэтому, если имеется дополнительная информация, позволяющая сузить 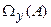 , её необходимо использовать. Чаще всего такая информация носит характер ограничений на искомое решение и может быть формализовано в виде задания некоторого множества М, которому должно принадлежать решение. При этом множество М не является классом единственности. Если это множество задано явно, например, в виде ограничений типа неравенств на возможные значения искомого параметра, то введение этой информации в критерий оптимальности может быть осуществлено уже описанным ранее (см. 5.2.1) способом:
, её необходимо использовать. Чаще всего такая информация носит характер ограничений на искомое решение и может быть формализовано в виде задания некоторого множества М, которому должно принадлежать решение. При этом множество М не является классом единственности. Если это множество задано явно, например, в виде ограничений типа неравенств на возможные значения искомого параметра, то введение этой информации в критерий оптимальности может быть осуществлено уже описанным ранее (см. 5.2.1) способом:
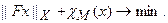 (5.86)
(5.86)
где:
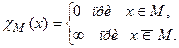
Однако в значительном числе случаев такая формулировка выглядит идеалистичной. Суть дела состоит в том, что наблюдаемая 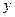 и информация, определяющая множество М, являются компонентами независимыми. Например, в качестве М может выступать класс эквивалентности для некоторого другого оператора
и информация, определяющая множество М, являются компонентами независимыми. Например, в качестве М может выступать класс эквивалентности для некоторого другого оператора 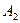 и другой наблюдаемой
и другой наблюдаемой 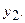 Это соответствует попытке найти общее решение для двух различных обратных задач относительно одной и той же содержательной модели среды. Целый ряд причин, включающий в себя несоответствие содержательных моделей в первой и второй задачах, наличие и независимость погрешностей (в том числе и систематических) в каждой из наблюдаемых, принципиальной ограниченностью множества М может привести к тому, что
Это соответствует попытке найти общее решение для двух различных обратных задач относительно одной и той же содержательной модели среды. Целый ряд причин, включающий в себя несоответствие содержательных моделей в первой и второй задачах, наличие и независимость погрешностей (в том числе и систематических) в каждой из наблюдаемых, принципиальной ограниченностью множества М может привести к тому, что 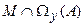 пусто и минимизация (86) на
пусто и минимизация (86) на 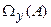 является бессодержательной задачей. В этих случаях целесообразно искать два элемента
является бессодержательной задачей. В этих случаях целесообразно искать два элемента 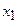 и
и 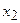 таких, что:
таких, что:
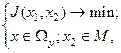 (5.87)
(5.87)
где 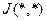 - некоторый функционал, определяющий меру близости
- некоторый функционал, определяющий меру близости 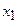 и
и 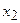 . Например
. Например 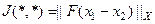 . Положим, что имеется наблюдаемая
. Положим, что имеется наблюдаемая 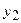 и
и 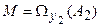 .
.
Пусть 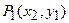 - оператор, ставящий в соответствие элементу
- оператор, ставящий в соответствие элементу 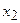 и наблюдаемой
и наблюдаемой 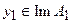 решение задачи:
решение задачи:
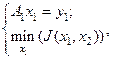 (5.88)
(5.88)
а 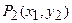 - оператор, ставящий в соответствие элементам
- оператор, ставящий в соответствие элементам 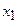 и
и 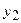 (что эквивалентно заданию
(что эквивалентно заданию  ) решение задачи:
) решение задачи:
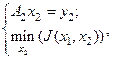 (5.89)
(5.89)
тогда, если пара 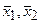 есть решения задачи:
есть решения задачи:
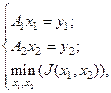 (5.90)
(5.90)
то необходимым условием, которому удовлетворяется эта пара, является:
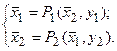 (5.91)
(5.91)
Зафиксировав некоторый элемент 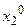 , рассмотрим итерационный процесс:
, рассмотрим итерационный процесс:
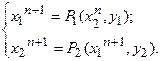 (5.92)
(5.92)
Из определения оператора 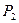 имеем:
имеем:
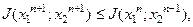 (5.93)
(5.93)
а из определения 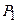 :
:
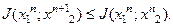 (5.94)
(5.94)
Соединяя эти два неравенства, получим:
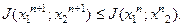 (5.95)
(5.95)
Если для некоторого n = N, (95) выполнено как равенство, то как равенства выполнены (94) и (93). Тогда если операторы 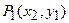 ,
, 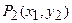 однозначны, то
однозначны, то 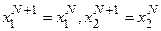 откуда
откуда
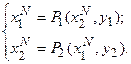
Следовательно, итерационный процесс (92) является монотонно сходящимся к решению задачи (90), а если уравнение (91) является дополнительно достаточным условием для решения задачи (90), то процесс (92) доставляет и решение задаче (90). Однако сходимость последовательности 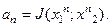 еще не влечет сходимости самих элементов
еще не влечет сходимости самих элементов 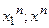 к некоторым элементам
к некоторым элементам 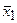 и
и 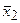 . Соотношением (95) обеспечена сходимость по функционалу. При определенной конструкции
. Соотношением (95) обеспечена сходимость по функционалу. При определенной конструкции 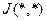 сходимость по
сходимость по 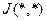 влечет и сходимость элементов
влечет и сходимость элементов 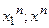 по норме, и в этих случаях процесс (92) полностью решает задачу (90).
по норме, и в этих случаях процесс (92) полностью решает задачу (90).
Обращаясь к построению операторов 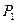 и
и 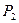 (88-89), легко видеть, что каждый из них есть ни что иное, как построение решения обратной задачи, оптимального относительно заданного фиксированного критерия оптимальности. Отсюда следует вывод, что методы решения частных обратных задач, основанные на критериальном подходе, естественным образом объединяются итерационным процессом (92) в процедуру совместного решения обратных задач. Но именно такого рода совместные решения обратных задач реализуют процедуру комплексной интерпретации. Постановка обратной задачи комплексной интерпретации (90), реализуемая процессом (92), состоит в нахождении пары элементов, каждый из которых удовлетворяет своей наблюдаемой и в своих классах эквивалентности выделяемая пара состоит из ближайших друг к другу элементов. Принципом комплексирования служит принцип максимальной близости друг к другу выделяемых элементов, при условии, что каждый из них удовлетворяет своему полю. Совсем не обязательно чтобы решение было одно и удовлетворяло обоим наблюдаемым. Такое положение дел, скорее, исключение, чем правило. Но пара элементов, являясь конкретно физическими моделям одного и того же объекта должна состоять из элементов, которые в каком то смысле близки друг к другу. Это достаточно общий и универсальный принцип комплексирования. В противном случае, если он не выполняется, теряется сам смысл использования нескольких методов для изучения одного объекта.
(88-89), легко видеть, что каждый из них есть ни что иное, как построение решения обратной задачи, оптимального относительно заданного фиксированного критерия оптимальности. Отсюда следует вывод, что методы решения частных обратных задач, основанные на критериальном подходе, естественным образом объединяются итерационным процессом (92) в процедуру совместного решения обратных задач. Но именно такого рода совместные решения обратных задач реализуют процедуру комплексной интерпретации. Постановка обратной задачи комплексной интерпретации (90), реализуемая процессом (92), состоит в нахождении пары элементов, каждый из которых удовлетворяет своей наблюдаемой и в своих классах эквивалентности выделяемая пара состоит из ближайших друг к другу элементов. Принципом комплексирования служит принцип максимальной близости друг к другу выделяемых элементов, при условии, что каждый из них удовлетворяет своему полю. Совсем не обязательно чтобы решение было одно и удовлетворяло обоим наблюдаемым. Такое положение дел, скорее, исключение, чем правило. Но пара элементов, являясь конкретно физическими моделям одного и того же объекта должна состоять из элементов, которые в каком то смысле близки друг к другу. Это достаточно общий и универсальный принцип комплексирования. В противном случае, если он не выполняется, теряется сам смысл использования нескольких методов для изучения одного объекта.
Дальнейшие рассмотрения связаны с конкретизацией вида функционала 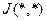 .
.
Пусть функционал 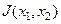 имеет вид:
имеет вид:
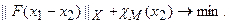 (5.96)
(5.96)
и множество 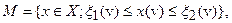 где
где 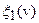 и
и 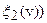 - заданные элементы.
- заданные элементы.
Выберем в качестве  пространство
пространство 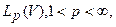 и пусть
и пусть 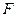 - линеен, непрерывен, и из условия
- линеен, непрерывен, и из условия 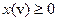 следует
следует 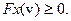 Обозначим
Обозначим 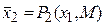 решение задачи:
решение задачи:
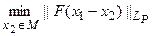 , (5.97)
, (5.97)
определенное условием:
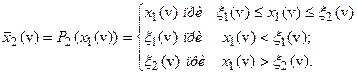 (5.98)
(5.98)
Эта процедура представляет собой поточечное проектирование значений функции 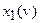 на множество
на множество  .
.
Доказательство. Пусть 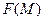 - образ множества М при отображении
- образ множества М при отображении 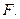
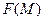 - замкнуто и выпукло, так как
- замкнуто и выпукло, так как 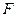 - взаимно-непрерывен и линеен. Тогда (97) можно переписать:
- взаимно-непрерывен и линеен. Тогда (97) можно переписать:
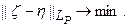 (5.99)
(5.99)
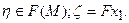
В соответствии с теоремой двойственности, для того, чтобы элемент 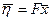 был решением задачи (99), необходимо и достаточно, чтобы в
был решением задачи (99), необходимо и достаточно, чтобы в 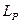 нашелся элемент
нашелся элемент 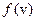 и:
и:
а) 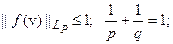
b) 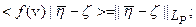 (5.100)
(5.100)
с) 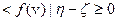
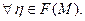
Чтобы были выполнены условия (100а), (100b), достаточно положить:
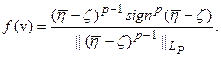 (5.101)
(5.101)
Остается проверить, что выполнено условие (100в) при выборе 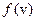 по правилу (101).
по правилу (101).
Подставляя (101) в (100в) и учитывая, что постоянный множитель роли не играет, получим:
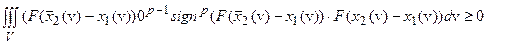
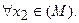 (5.102)
(5.102)
Рассмотрим подынтегральное выражение. Пусть  - произвольная точка области
- произвольная точка области 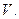 Возможны случаи:
Возможны случаи:
1) 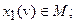
2) 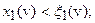
3) 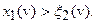
В первом, в соответствии с правилом (98), подынтегральное выражение равно нулю. Во втором случае 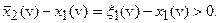 Но тогда для любых
Но тогда для любых 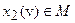 имеем
имеем 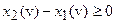 и, следовательно, подынтегральное выражение положительно, поскольку
и, следовательно, подынтегральное выражение положительно, поскольку 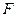 сохраняет знак функции. В случае (3) имеем:
сохраняет знак функции. В случае (3) имеем: 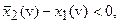 и тогда
и тогда 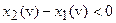 для любого
для любого 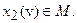

Снова оказывается, что подынтегральное выражение положительно. Поскольку точка  была произвольной, то всюду в V подынтегральное выражение в (102) или что то же самое (100в), выполнено.
была произвольной, то всюду в V подынтегральное выражение в (102) или что то же самое (100в), выполнено.
В приведенном случае оператор проектирования выглядит особенно просто, и учет ограничений типа неравенств при решении обратной задачи в рамках критериального подхода, в соответствии с (92) сводится к итеративному решению обратной задачи без ограничений и проектированию результата множество М по правилу (98).
Рассмотрим далее частный случай задачи (90).
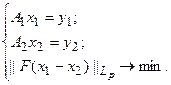 (5.103)
(5.103)
Делая замену переменных 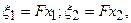 получаем:
получаем:
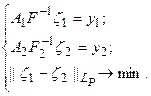 (5.104)
(5.104)
Ограничимся случаем  . Будем предполагать далее, что
. Будем предполагать далее, что 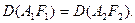
Задача (104) легко сводится к следующей:
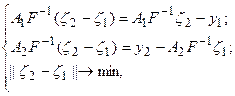 (5.104а)
(5.104а)
или:
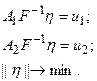 (5.104b)
(5.104b)
Здесь 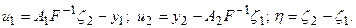
Обозначим В – линейный ограниченный оператор из  в
в 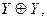 где
где 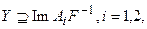 определенный отношением:
определенный отношением:
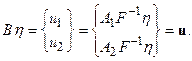
Тогда:
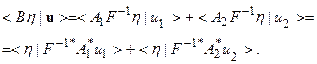
Откуда приходим к выводу, что:
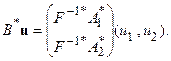
Применяя теперь к задаче (104b) результаты из п. 5.3, получаем:
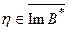 .
.
Характеризация почти идеального экстремального класса 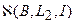 задана уравнением
задана уравнением
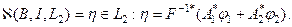 (5.105)
(5.105)
Однако уравнение (105) еще не позволяет найти 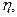 поскольку для нахождения элементов
поскольку для нахождения элементов 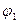 и
и 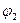 , входящих в описание
, входящих в описание 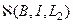 необходимо знание правых частей в (104b). Уравнение (105) важно с точки зрения того, что оно выражает необходимое и достаточное условие для
необходимо знание правых частей в (104b). Уравнение (105) важно с точки зрения того, что оно выражает необходимое и достаточное условие для 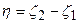 и поэтому:
и поэтому:
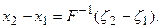
Зафиксируем элемент 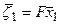 в (104). Тогда
в (104). Тогда 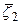 есть решение задачи:
есть решение задачи:
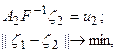 (5.106)
(5.106)
и, следовательно,
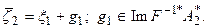 (5.107)
(5.107)
Если зафиксирован элемент 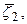 то
то 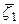 есть решение задачи:
есть решение задачи:
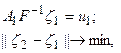 (5.108)
(5.108)
откуда:
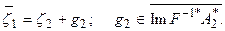 (5.109)
(5.109)
Поскольку 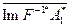 и
и 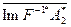 - суть линейные подпространства, то из (109) и (107) получаем:
- суть линейные подпространства, то из (109) и (107) получаем:
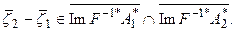 (5.110)
(5.110)
Рассмотрим возможные случаи, обозначая для простоты: 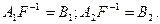 Если:
Если:
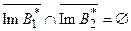
то, переходя к ортогональным дополнениям (прил.2.4), получим:
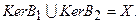 (5.111)
(5.111)
Таким образом, условия 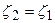
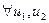 и
и 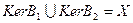 - эквивалентны. Однако из того, что
- эквивалентны. Однако из того, что 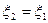 , не следует выражение для решения задачи (104). Предположим, что дополнительно
, не следует выражение для решения задачи (104). Предположим, что дополнительно 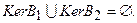 Последнее требование означает, что ядро оператора:
Последнее требование означает, что ядро оператора:
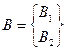
Состоит только из нуля и, следовательно, решение задачи:
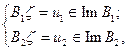 (5.112)
(5.112)
на 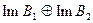 существует и единственно. Единственность решения – факт очевидный. Показать надо существование решения при
существует и единственно. Единственность решения – факт очевидный. Показать надо существование решения при 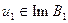 и
и 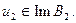 Если
Если 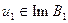 и
и 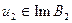 , но решения задачи (112) не существует, то это эквивалентно тому, что не существует решения задачи:
, но решения задачи (112) не существует, то это эквивалентно тому, что не существует решения задачи:
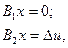 (5.113)
(5.113)
