Решение задачи построения модели для одного шага интегрирования методами Эйлера и Рунге-Кутта
Начальные условия
Для решения задачи построения модели расчета траектории неуправляемого летательного аппарата на одном шаг интегрирования системы, определяющей движение ЛА в начале активного участка траектории, методами Эйлера и Рунге - Кутта начальными условиями будут:
· шаг интегрирования h равняется 0.01 с. (h=0.01 с.);
· начальный момент времени 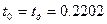
· скорость ЛА 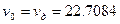 в момент схода с направляющих;
в момент схода с направляющих;
· угол наклона направляющих 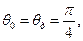
· начальная абсцисса 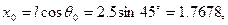
· начальная ордината 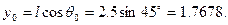
Расчет системы уравнений методом Эйлера
Рассмотрим уравнения движения в проекциях на касательную и нормаль к траектории:
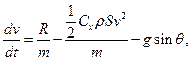 (1)
(1)
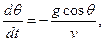 (2)
(2)
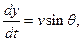 (3)
(3)
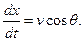 (4)
(4)
при начальных условиях: 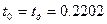
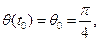
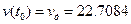 ;
;
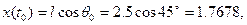
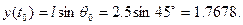
Примем за шаг интегрирования 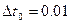 с.
с.
По известным начальным условиям определим значения производных 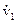 ,
, 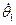 ,
, 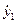 ,
, 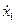 в начальной точке где
в начальной точке где 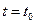 :
:
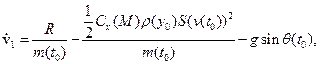
где 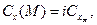 где
где 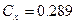
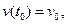
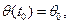
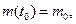
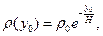 где H=7800 м,
где H=7800 м,
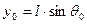
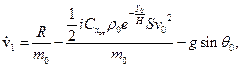
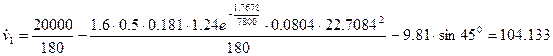
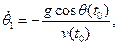
где 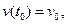
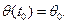
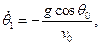
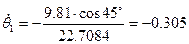
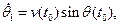
где 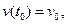
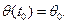
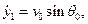
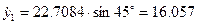
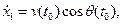
где 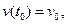
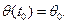
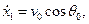
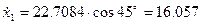
Определим новое значение функций 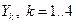 :
:
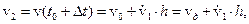
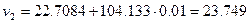
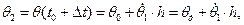
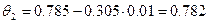
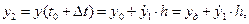
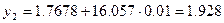
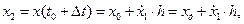
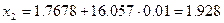
Расчет системы уравнений методом Рунге-Кутта
Рассмотрим уравнения движения в проекциях на касательную и нормаль к траектории:
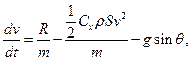 (1)
(1)
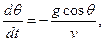 (2)
(2)
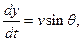 (3)
(3)
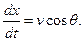 (4)
(4)
при начальных условиях: 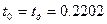
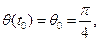
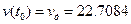
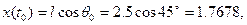
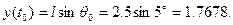
Примем за шаг интегрирования 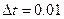 с.
с.
Пусть 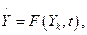 где
где 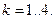
При 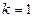 :
: 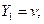
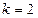 :
: 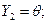
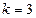 :
: 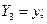
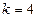 :
: 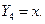
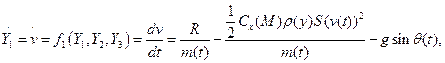
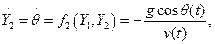
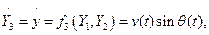
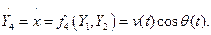
Будем рассматривать систему трёх дифференциальных уравнений для определения v, θ и y, а x определять после определения v, θ и y.
По известным начальным условиям определим значения производных 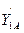 ,
, 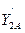 ,
, 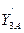 в начальной точке А, где
в начальной точке А, где 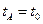 :
:
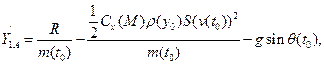
где 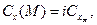 где
где 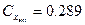
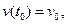
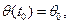
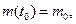
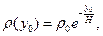 где H=7800 м,
где H=7800 м,
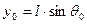
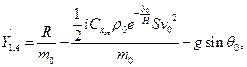
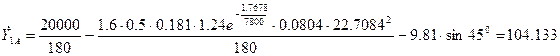
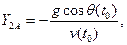
где 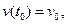
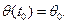
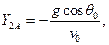
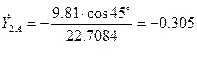
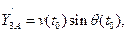
где 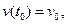
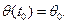
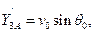
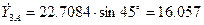
Из начальной точки A проведём прямую 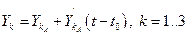 и отметим значение её ординаты в середине шага интегрирования
и отметим значение её ординаты в середине шага интегрирования 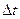 (точка B с координатами
(точка B с координатами 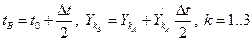 ):
):
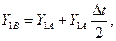
где 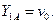
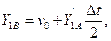
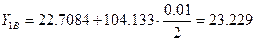
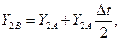
где 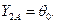
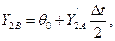
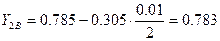
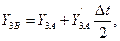
где 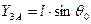
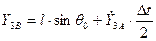
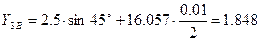
Найдём значения производных 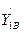 ,
, 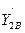 ,
, 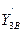 в точке B:
в точке B:
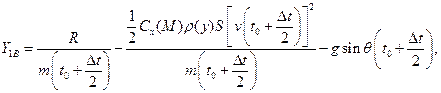
где 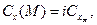 где
где 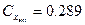
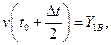
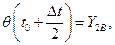
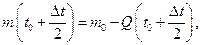
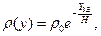 где H=7800 м,
где H=7800 м, 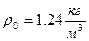
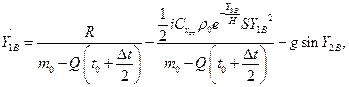
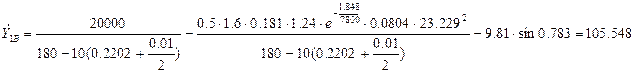
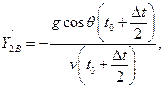
где 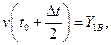
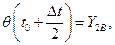
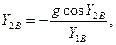
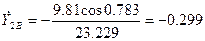
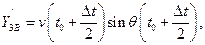
где 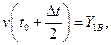
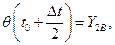
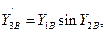
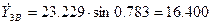
Проведём из точки А прямую 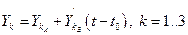 и отметим значение её ординаты в середине шага интегрирования
и отметим значение её ординаты в середине шага интегрирования 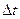 (точка С с координатами
(точка С с координатами 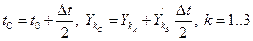 ):
):
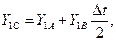
где 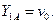
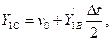
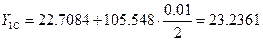
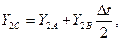
где 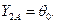
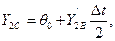
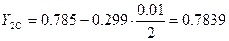
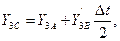
где 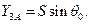
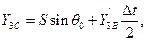
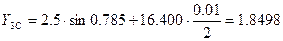
Найдём значения производных 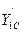 ,
, 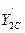 ,
, 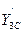 в точке С:
в точке С:
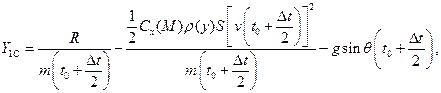
где 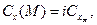 где
где 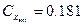
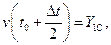
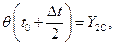
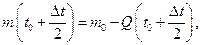
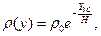 где H=7800 м,
где H=7800 м, 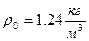
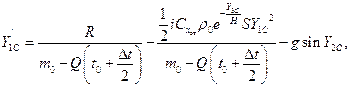
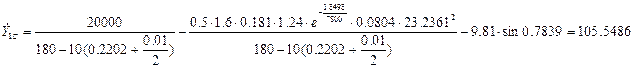
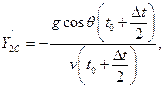
где 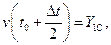
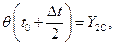
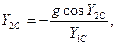
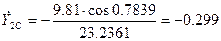
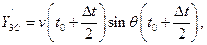
где 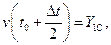
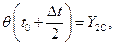
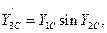
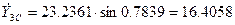
Проведём из точки А прямую 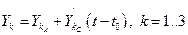 и отметим значение её ординаты в конце шага интегрирования
и отметим значение её ординаты в конце шага интегрирования 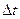 (точка D с координатами
(точка D с координатами 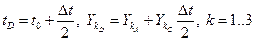 ):
):
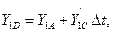
где 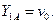
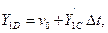
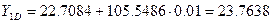
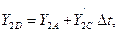
где 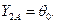
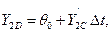
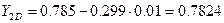
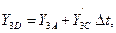
где 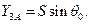
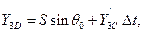
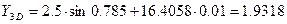
Найдём значения производных 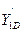 ,
, 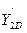 ,
, 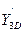 в точке D:
в точке D:
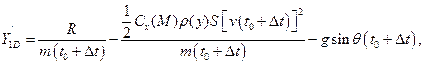
где 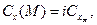 где
где 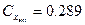
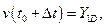
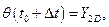
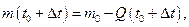
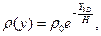 где H=7800 м,
где H=7800 м, 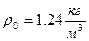
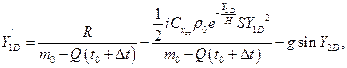
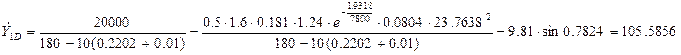
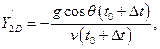
где 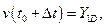
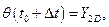
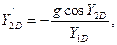
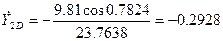
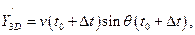
где 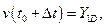
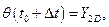
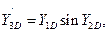
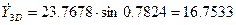
5. Согласно расчётным формулам метода Рунге-Кутта 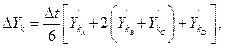
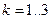 :
:
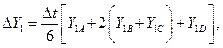
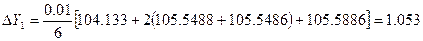
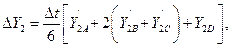
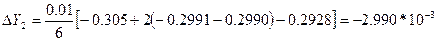
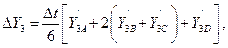
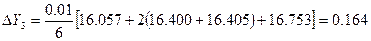
Определим новое значение функций 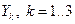 :
:
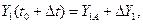
где 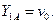
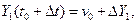
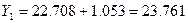
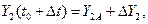
где 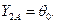
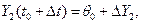
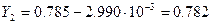
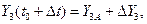
где 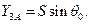
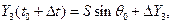
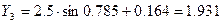
Определим новое значение функции 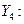
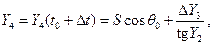

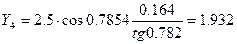
Сравнение решений тестового примера на 1 шаг, полученных без ПК
Сравнение результатов производится в соответствии с данными, представленными в таблице 6:
Таблица 6
| Обозначения | 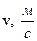 | 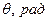 | 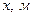 | 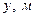 |
| Ручной счет методом Эйлера | 23.749 | 0.782 | 1.928 | 1.928 |
| Ручной счет методом Рунге-Кутта | 23.761 | 0.782 | 1.931 | 1.932 |
Результаты расчета траекторных параметров неуправляемого ЛА
Движение по направляющим
Результатами расчета траекторных параметров данного участка траектории являются значения дульной скорости vд и дульного времени tд (см. Таблица 3).
