Монотонно возрастающие и убывающие функции

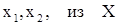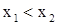Функция f(x) называется возрастающейна множестве Х, если для произвольных при выполняется неравенство 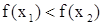, т.е. большему значению аргумента соответствует большее значение функции. Например, 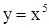, 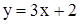- возрастают. Функция f(x) называется убывающей,если, наоборот, большему значению аргумента соответствует меньшее значение функции: при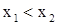 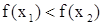. Например: 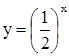, 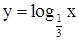. Возрастающие и убывающие функции называют строго монотонными.

Четные и нечетные функции

Числовое множество Х называется симметричным, если для произвольного 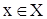элемент . Например, множество целых чисел, действительных чисел, отрезок [-а, а]. Функция f, определенная на симметричном множестве Х, называется четной, если . Например: 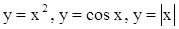. График четной функции симметричен относительно оси OY.

Функция f, определенная на симметричном множестве Х, называется нечетной , если 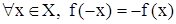. Например: 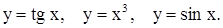График нечет-ной функции симметричен относительно точки О(0,0) – начала координат. Функция может быть нечетной, ни нечетной, например: .

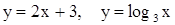Периодические функции

Пусть f определена на множестве Х. Если существует 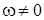такое, что 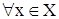числа 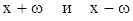также принадлежат множеству Х и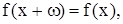 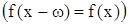, то функцию f называют периодическойс периодом .

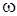Примеры:

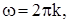1) периодическая с периодом где ;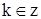

2) периодическая с периодом где ;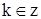

3) дробная часть числа: 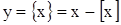- периодическая, .

Установление факта периодичности функции существенно облегчает ее изучение и построение графика: периодическую функцию можно исследовать в пределах одного периода. Для построения графика периодической функции с периодом 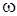достаточно построить график этой функции на интервале 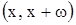, а затем полученный график периодически продолжить. Рассмотрим некоторые примеры на установление периодичности функции.

Пример.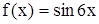

Существует ли такое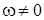 ,чтобы для всех действительных х выполнялосьусловие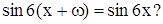

Имеем 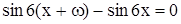, , 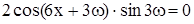это выполняется при 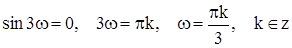. Следовательно, такие 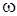существуют, функция является периодической, наименьший ее положительный период .

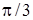Пример 2. .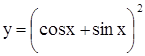

Имеем 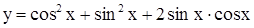или 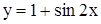- периодическая функция с периодом .

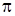Ограниченные и неограниченные функции

Функция f, определенная на множестве Х, называется ограниченной на множестве 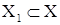, если множество ее значений f(x) на множестве 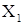ограничено, т.е. существуют постоянные m и М такие, что 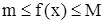. В противном случае функция называется неограниченной.

Примеры:

1) 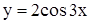ограничена на всей числовой оси, т.к. ;

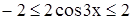2) функция 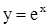ограничена снизу, так как ;

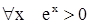3) функция 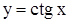ограничена на промежутке 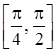, но ограничена на про-межутке .

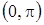Системы координат

В плоскости, где изображен график функции, можно ввести две системы координат: декартову систему координат и полярную систему координат.

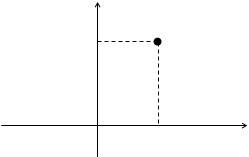
1. Декартова система координат (или прямоугольная) определяется линей- ной единицей измерения и двумя взаимно перпендикулярными числовыми осями. Точка пересечения осей называется началом координат, а оси – координатными осями. Одна из них – ось ОХ или ось абсцисс, а другая – ось OY или ось ординат. С каждой точкой Р плоскости, в которой выбрана система координат, можно связать два числа, которые получаем следующим образом (рис. 1.4). Опускаем из точки Р перпендикулярны на оси координат.

Y

P_y P(x,y)

P_x x

Рис. 1.4

Пусть Р_х – основание перпендикуляра на оси абсцисс, а Р_у – основание перпендикуляра на оси ординат. Точке Р_х соответствует действительное число х на оси ОХ, а точке Р_у – число на оси ОУ. Эти числа называют координатами точки Р: x – абсциссой и у – ординатой.

Каждую пару действительных чисел можно рассматривать как координаты некоторой точки на плоскости. Чтобы построить точку по её координатам х₀ и у₀, на плоскости надо отложить числа х₀ и у₀ соответственно на осях ОХ и ОУ, а затем из этих точек провести перпендикуляры к осям. Точка пересечения перпендикуляров будет искомой.

2. Полярная система координат. Полярные координаты точки на плоскости – это два числа, которые определяют положение этой точки относительно некоторой фиксированной точки О (полюса) и некоторого фиксированного луча 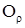(поляр-ной оси).

Первая координата 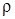точки М(r, 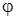) – полярный радиус – определяет расстояние точки от полюса: 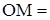r; вторая координата 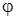- полярный угол – угол, на который надо повернуть ось 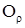в положительном или отрицательном направлении до совпадения с лучом ОМ (рис.1.5).

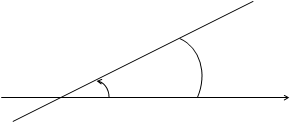
P

M

j

0 r

Рис. 1.5

Полярный угол считается положительным при отсчете от полярной оси против часовой стрелки и отрицательным – при отсчете в противоположную сторону.

Если в полярной системе координат условимся длину полярного радиуса считать неотрицательной ( 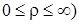и полярный угол брать в интервале 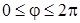, то этим устанавливается взаимно однозначное соответствие между точками плоскости и полярными координатами 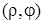за исключением полюса, который конкретного полярного угла не имеет. Это соответствие удобно иметь в виду при решении задач на построение отдельных точек на плоскости, определение расстояния между двумя точками, деление отрезка в заданном отношении и др.

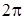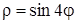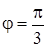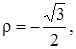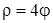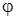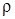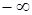При исследовании функций и построении их графиков часто полярный радиус принимает отрицательные значения, а полярный угол – значения, большие , или отрицательные. Например, у функции при полярный радиус а у функции угол может принимать произвольные значения. Во многих задачах приходится рассматривать значения полярного угла и полярного радиуса от до 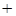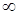. Отрицательные значения 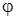откладывают от полярной оси по часовой стрелке, а отрицательные значения 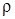– на продолжении луча ОР с другой стороны от полюса.

Переход от декартовых координат к полярным и наоборот выполняется по формулам

,

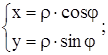
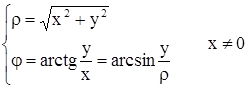где х, у – декартовы координаты произвольной точки М(х,у), а 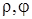- её полярные координаты.

Здесь декартова система координат выбрана так, чтобы её начало О совпадало с полюсом полярной системы, а ось ОХ – с полярной осью.