Образец выполнения лабораторной работы №10

(Численное дифференцирование)

Постановка задачи. Функция задана в равноотстоящих узлах своими значениями 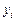в узлах 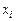. Найти приближенное значение первой и второй производных функции при заданном значении аргумента 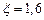, где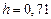

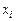		1,71	2,42	3,13	3,84	4,55	5,26
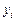	0,778801	1,906915	3,19803	4,479744	5,645985	6,637627	7,42804

Так как функция дана в равноотстоящих узлах и 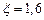находится в начале таблицы, то используем первую интерполирующую формулу Ньютона. Для этого найдем конечные разности .

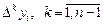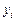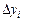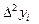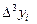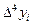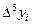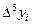0,778801	1,128114	0,163001	-0,1724	0,06633	-0,01938	0,004936
1,906915	1,291115	-0,0094	-0,10607	0,046946	-0,01445
3,19803	1,281714	-0,11547	-0,05913	0,032498
4,479744	1,166241	-0,1746	-0,02663
5,645985	0,991641	-0,20123
6,637627	0,790414
7,42804

Используя полученные конечные разности выпишем интерполирующий полином Ньютона 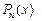. Полагая 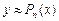, , 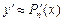, 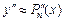вводя обозначение 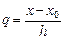получим ,

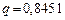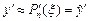	1,714043		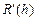	0,005325
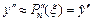	0,377144		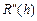	0,007478

Определим число верных знаков в широком смысле, тогда получим

, ,

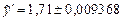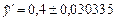тогда точные значения должны принадлежать отрезкам

, .

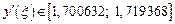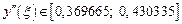Действительно, так как точные и соответствующие погрешности принимают значения

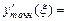	1,716019		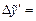	0,001977
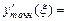	0,375379		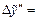	0,001764

при этом выполняются неравенства , .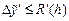

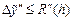Таким образом найденные значения производных отвечают точным значениям в пределах найденных погрешностей приближенных значений.

Замечание. Очевидно, что в случае когда значение 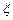находится ближе к концу таблицы значений функции необходимо применить вторую интерполирующую формулу Ньютона, в противном случае погрешность полученного приближенного значения производной будет большой

Лабораторная работа № 11

Тема: Численное интегрирование.

Задание:

d)Найти приближенное значение интеграла по формулам левых и правых прямоугольников с точностью .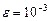

e)Найти приближенное значение интеграла по формуле средних прямоугольников с точностью .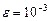

f)Найти приближенное значение интеграла по формуле трапеции с точностью .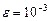

g)Найти приближенное значение интеграла по формуле Симпсона с точностью .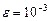

h)Сравнить полученные результаты.

Вопросы самоконтроля.

Постановка задачи. Геометрическая иллюстрация.

Основная идея приближенного численного интегрирования.

Формулы Ньютона - Котеса.

Численное интегрирование методами прямоугольников (левого, правого, среднего), погрешность метода.

Численное интегрирование методом трапеции, погрешность метода.

Численное интегрирование методом Симпсона, погрешность метода.

Сравнение методов.

Интегралы для вычисления определяются исходя их номера варианта

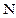( - номер варианта или последние (одна или две) цифры зачетки студента).

Варианты	a)	b)
№1 - №10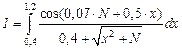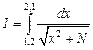
№11 - №20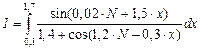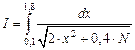
№21 - №30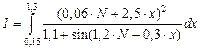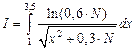
№31 - №40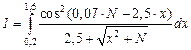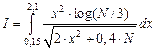
№41 - №50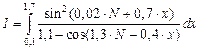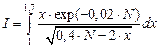
№51 - №60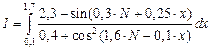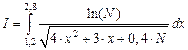