Критерии оптимальности типа нормы
Рассмотрим теперь обобщающую (11-12) задачу. Обобщение распространим как на вид решаемого уравнения, так и на характер используемого для этой цели критерия оптимальности в рамках вариационного принципа доопределения задачи.
Пусть имеется операторное уравнение с замкнутым оператором:
 . . | (5.16) |
Действующим из банахова пространства X в банахово пространство Y и  . Пусть, далее, класс эквивалентности
. Пусть, далее, класс эквивалентности  [19] содержит более одного элемента. Дальнейшие рассмотрения связаны с задачей:
[19] содержит более одного элемента. Дальнейшие рассмотрения связаны с задачей:
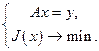 | (5.17) |
где 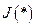 - сильновыпуклый на
- сильновыпуклый на 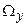 функционал, являющийся выражением априорной информации об искомом решении уравнения (16). Постановку (17) называем критериальным подходомк решению обратной задачи, а методы решения этой задачи – критериальными методами решения обратных задач. Если
функционал, являющийся выражением априорной информации об искомом решении уравнения (16). Постановку (17) называем критериальным подходомк решению обратной задачи, а методы решения этой задачи – критериальными методами решения обратных задач. Если 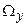 содержит один элемент, то задача (17) оказывается эквивалентной решению операторного уравнения (16), для чего применимы уже изложенные ранее методы решения некорректных задач. Чем шире множество
содержит один элемент, то задача (17) оказывается эквивалентной решению операторного уравнения (16), для чего применимы уже изложенные ранее методы решения некорректных задач. Чем шире множество 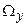 , тем в большей мере свойства решения (17) определены видом выбранного функционала
, тем в большей мере свойства решения (17) определены видом выбранного функционала 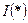 .
.
5.2.1. Вариационные параметризациии квазирешения.
Постановкой (17) может быть учтена принадлежность искомого решения заданному классу модельному классу. Действительно, пусть М - класс моделей, на котором ищется решение задачи (16). Положим:
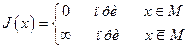 | (5.18) |
При таком выборе критерия оптимальности задача (17) оказывается эквивалентной поиску решения на М, которое следует искать как квазирешение. Однако необходимо учитывать приближенность задания исходных данных, в чем собственно и состоит идея построения квазирешения - нахождение элемента из модельного класса, минимизирующего невязку. Покажем, что “реалистичные” постановки обратных задач, учитывающих приближенность данных, могут быть сформулированы с использованием (17).
Поскольку наблюдаемая 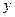 задана с ошибками, подчиненными некоторому вероятному закону, вид которого нас пока не интересует, то реально следует говорить не о требовании равенства
задана с ошибками, подчиненными некоторому вероятному закону, вид которого нас пока не интересует, то реально следует говорить не о требовании равенства  , а о выполнении условия:
, а о выполнении условия: 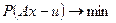 , где P - некоторый функционал на Y. Тем более, это условие надо использовать еще и потому, что из-за ошибок в наблюдаемой следует предполагать, что
, где P - некоторый функционал на Y. Тем более, это условие надо использовать еще и потому, что из-за ошибок в наблюдаемой следует предполагать, что 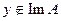 . Таким образом, “реалистичная”, учитывающая приближенность входных данных постановка задачи (17) такова:
. Таким образом, “реалистичная”, учитывающая приближенность входных данных постановка задачи (17) такова:
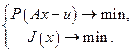 | (5.19) |
Два принципа оптимальности в (19) отражают принципиально разные оптимизируемые компоненты. Оптимальность 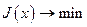 , относится к параметрам модели среды. Она отражает тот факт, что искомый элемент в классе себе эквивалентных по полю обладал свойством оптимальности
, относится к параметрам модели среды. Она отражает тот факт, что искомый элемент в классе себе эквивалентных по полю обладал свойством оптимальности 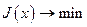 . Оптимальность
. Оптимальность 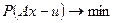 , относится к качеству подбора поля. Она требует, чтобы в классе элементов из оптимальных по
, относится к качеству подбора поля. Она требует, чтобы в классе элементов из оптимальных по  элементов, соответствующих различным полям, был отобран такой, поле от которого удовлетворяет критерию
элементов, соответствующих различным полям, был отобран такой, поле от которого удовлетворяет критерию 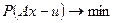 . Это принципиально разные критерии и смешивать их ни в коем случае нельзя. Для того чтобы согласовать два принципа оптимальности в (19), построим такую конструкцию. Зафиксируем некоторый элемент
. Это принципиально разные критерии и смешивать их ни в коем случае нельзя. Для того чтобы согласовать два принципа оптимальности в (19), построим такую конструкцию. Зафиксируем некоторый элемент 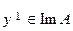 и решим задачу (17), получив некоторый элемент
и решим задачу (17), получив некоторый элемент 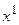 . Если ее решение существует и единственно, что происходит, например, при сильной выпуклости
. Если ее решение существует и единственно, что происходит, например, при сильной выпуклости  на
на 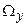 , то
, то 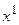 - это единственный элемент, соответствующий
- это единственный элемент, соответствующий 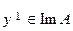 . Выбрав новый элемент
. Выбрав новый элемент 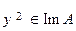 , повторим при тех же условиях решение задачи (17), получив, таким образом, другой единственный элемент
, повторим при тех же условиях решение задачи (17), получив, таким образом, другой единственный элемент 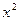 . Повторяя этот процесс для всех
. Повторяя этот процесс для всех 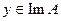 , получим множество
, получим множество  решений задачи (17) при всех у из
решений задачи (17) при всех у из  . Это множество называется экстремальным классомдля оператора A, соответствующего функционалу
. Это множество называется экстремальным классомдля оператора A, соответствующего функционалу  . Поскольку функционал
. Поскольку функционал  таков, что решение задачи (17) существует и единственно при каждом
таков, что решение задачи (17) существует и единственно при каждом  , то полученное множество
, то полученное множество  оказывается во взаимнооднозначном соответствии с
оказывается во взаимнооднозначном соответствии с  и образует класс единственности для уравнения
и образует класс единственности для уравнения  . Принадлежность элемента
. Принадлежность элемента  множеству
множеству  автоматически означает, что элемент
автоматически означает, что элемент  в своем классе эквивалентности
в своем классе эквивалентности 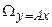 , минимизирует функционал
, минимизирует функционал  . Эквивалентной задаче (19) теперь служит задача:
. Эквивалентной задаче (19) теперь служит задача:
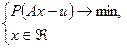 | (5.20) |
Таким образом, оба принципа оптимальности в (19) согласованы. Для того чтобы решить задачу (17) в “реалистической” постановке, достаточно решить ее для всех 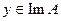 , построив класс
, построив класс  , и далее решать задачу (20).
, и далее решать задачу (20).
