Практическая работа № 3

Тема: Равносильные преобразования формул алгебры логики

с помощью законов логики

Цели работы:

3) научиться строить таблицу истинности формулы логики;

4) научиться применять методику упрощения формул логики с помощью равносильных преобразований.

Пояснения:

Всякое суждение, утверждающее что-либо о чем-либо, называют высказыванием, если можно сказать, истинно оно или ложно в данных условиях места и времени.

В русском языке сложные предложения получают из двух других с помощью союзов «и», «а», «если... то», «либо», «или», «тогда и только тогда, когда», «не», «неверно, что». Назовем такие союзы логическими связками.

Тогда утвердительные предложения, не содержащие (содержащие) логические связки, называют элементарными высказываниями (составными).

Если простое высказывание является истинным, то ему соответствует значение логической переменной 1. Если простое высказывание является ложным, то ему соответствует значение логической переменной 0. Для того чтобы определить, истинно или ложно некоторое сложное высказывание, используют таблицы истинности,

Логические операции

Отрицанием высказывания А называется высказывание 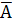, которое истинно, когда высказывание А ложно, и ложно, когда А истинно.

Дизъюнкцией высказываний А и В называется высказывание A Ú В, которое истинно тогда и только тогда, когда истинно хотя бы одно из этих высказываний.

Конъюнкцией высказываний А и В называется высказывание А Ù В, которое истинно тогда и только тогда, когда истинны оба высказывания.

Импликацией высказываний А и В называется высказывание А → В, которое ложно тогда и только тогда, когда из истины следует ложь.

Эквиваленцией высказываний А и В называется высказывание А ↔ В, которое истинно тогда и только тогда, когда либо истинны, либо ложны одновременно оба высказывания.

Равносильные формулы

1)

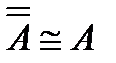
2)

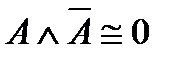
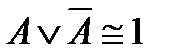
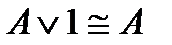
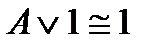
3)

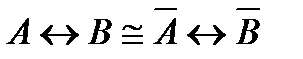
4)

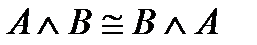
5)

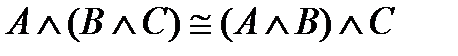
6)

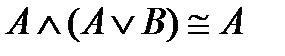
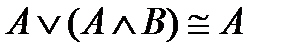
7)

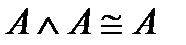
8)

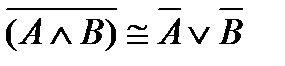
9)

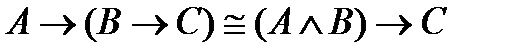
10)

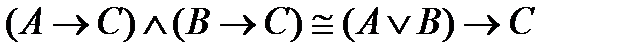
11)

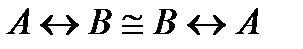
12)

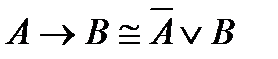
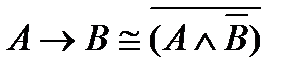
13)

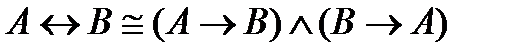
14)

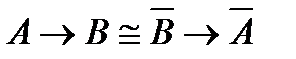
Оборудование, аппаратура, материалы и их характеристики:персональные компьютеры с лицензионным программным обеспечением; доска, маркеры; рабочие тетради; раздаточный материал.

Порядок выполнения работы:

Студенты получают задания по вариантам. Метод решения выбирается студентами самостоятельно и зависит от приобретенных в процессе обучения навыков. В процессе выполнения практической работы преподаватель проводит как групповые, так и индивидуальные консультации по вопросам дополнительного разъяснения отдельных понятий и аспектов изученных тем, задания и оформления отчета.

1. Используя таблицы истинности, докажите следующие эквивалентности:

Таблица 1 – Задание № 1

№ варианта	Исходные данные

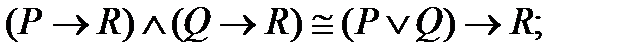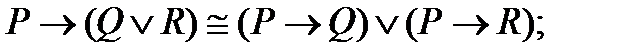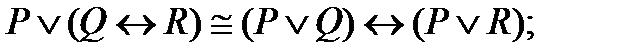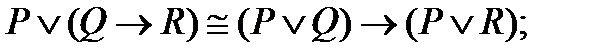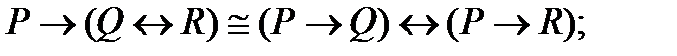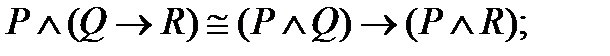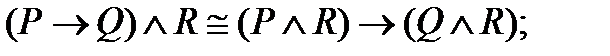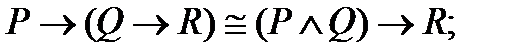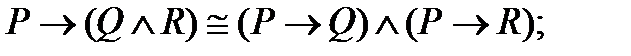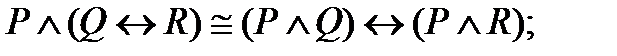2. Упростите высказывания и сравните таблицы истинности условия и ответа. Сделайте вывод об истинности:

Таблица 2 – Задание № 2

№ варианта	Исходные данные

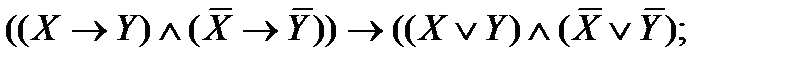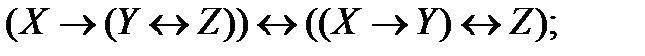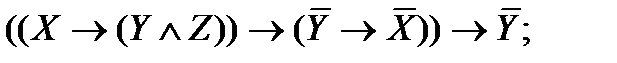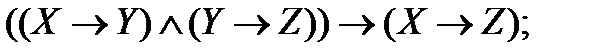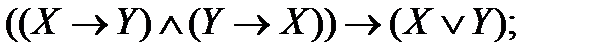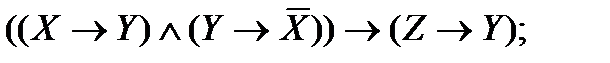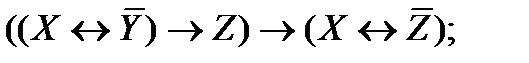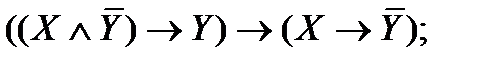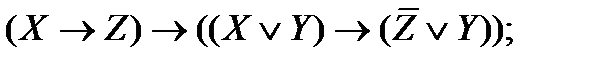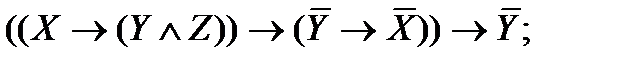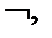
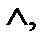
3. Записать формулы в приведенном виде (содержащим только операции над простыми переменными).

Таблица 3 – Задание № 3

№ варианта	Исходные данные

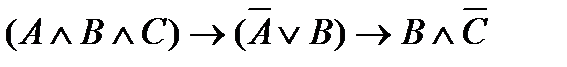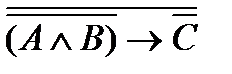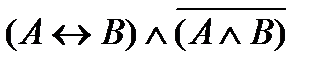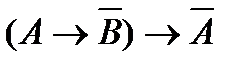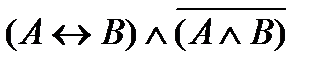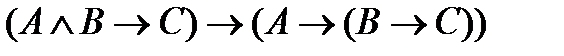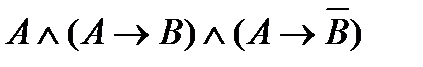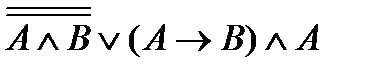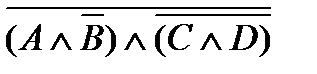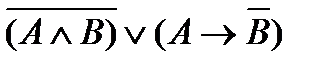Требования к отчету: Отчет должен содержать:

- название практической работы;

- формулировку цели работы;

- краткие теоретические сведения по теме работы в виде таблиц, графиков, диаграмм, схем, рисунков и формул;

- результаты решения заданий;

- выводы по работе;

- краткие письменные ответы на контрольные вопросы.

Текст отчета набирается на компьютере. Допускается тип шрифта Times New Roman, размер 12 – 14, межстрочный 1,5 интервал, выравнивание текста по ширине странице, абзацный отступ 1,25.

Контрольные вопросы:

1) Как сложные высказывания образуются из простых?

2) Что такое пропозициональные связки? Какие пропозициональные связки вы знаете?

3) Чем отличается конъюнкция от дизъюнкции (как логическая связка)?

4) Чем отличается строгая дизъюнкция от нестрогой (как логическая связка)?

5) Чем отличается импликация от эквиваленции (как логическая связка)?

6) Какие формулы называются выполнимыми? Тождественно-ложными? Тождественно-истинными? Опровержимыми?

Учебная и специальная литература:

1) Спирина М.С., Спирин В.В. Дискретная математика: Учебник. – М.: Издательский центр «Академия», 2009. – 370 с.

2) Игошин В.И. Задачи и упражнения по математической логике и теории алгоритмов: учеб. пособие для высш. учеб. заведений. – М.: Издательский центр «Академия», 2009. – 304 с.

3) Тишин В.В. Дискретная математика в примерах и задачах. – СПб.: БХВ – Петербург, 2008. – 352 с.