Качественные характеристики эвольвентного
Зацепления
Коэффициент перекрытия
Коэффициентом перекрытия называется отношение длины активной линии зацепления к основному шагу зубчатого колеса, он обозначается 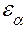 и определяется отношением
и определяется отношением
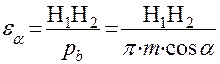 .
.
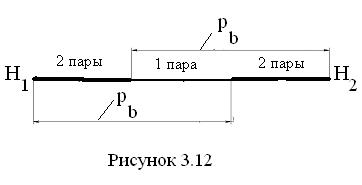
Передача движения в зубчатом зацеплении происходит таким образом, что, прежде чем предыдущая пара зубьев выйдет из зацепления (из контакта), последующая должна войти в зацепление (в контакт). Чем раньше она вступит в зацепление, тем более плавно работает передача. Количественной характеристикой этого качества и является коэффициент перекрытия, т. е. он, по существу, характеризует плавность работы зубчатой передачи. Обычно величина коэффициента перекрытия заключена между 1 и 2, при этом минимальное значение не должно быть меньше 1,1. Схематически соотношение между длиной активной лини зацепления и основным шагом показано на рис. 3.12. Точка контакта профилей зубьев перемещается вдоль активной линии зацепления от точки H1 к точке H2. Основной шаг короче активной линии зацепления, поэтому в пределах этой линии работают то одна, то две пары зубьев. Если отложить, как показано на рис. 3.12, основной шаг pb от точек H1 и H2, то отрезок H1H2 будет разделён на три части. Две крайние части соответствуют зонам двухпарного зацепления зубьев, а средняя – зоне однопарного зацепления. Чем короче средняя зона, тем плавнее работает зубчатая передача, так как суммарная длина двух крайних участков становится длиннее.
Удельное скольжение
Удельным скольжением называется отношение скорости скольжения профилей в точке их касания к скорости перемещения точки касания по профилю. Этот показатель характеризует износ зубьев в результате трения скольжения их боковых (рабочих) поверхностей. Возьмём точки К1 первого профиля и К2 второго профиля, 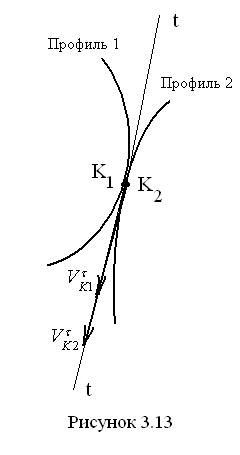 совпадающие в данный момент друг с другом (рис. 3.13). В этих точках профили имеют общую касательную t – t, вдоль которой направлены касательные (тангенциальные) составляющие их абсолютных скоростей. В общем случае эти скорости отличаются друг от друга по величине, могут отличаться и по направлению, оставаясь на общей касательной. Разность величин этих скоростей составляет скорость скольжения в контакте зубьев.
совпадающие в данный момент друг с другом (рис. 3.13). В этих точках профили имеют общую касательную t – t, вдоль которой направлены касательные (тангенциальные) составляющие их абсолютных скоростей. В общем случае эти скорости отличаются друг от друга по величине, могут отличаться и по направлению, оставаясь на общей касательной. Разность величин этих скоростей составляет скорость скольжения в контакте зубьев.
Согласно определению, удельное скольжение выразится двумя математическими выражениями, относящимися к разным колёсам:
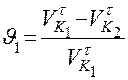 и
и 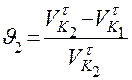 .
.
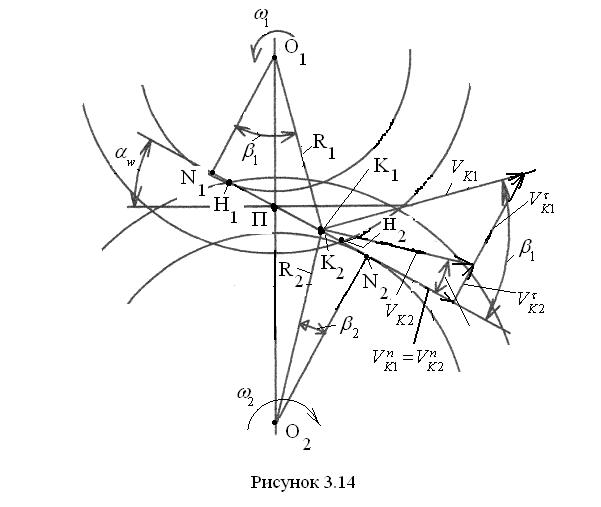
Для определения тангенциальных составляющих скоростей обратимся к
рис. 3.14. Соединим точку К1 с центром О1 вращения колеса 1 радиусом R1, и точку К2, совпадающую с точкой К1, с центром О2 радиусом R2. Перпендикулярно радиусу R1 в сторону вращения колеса 1 отложим абсолютную скорость точки К1, равную 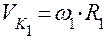 , и перпендикулярно радиусу R2 в сторону вращения колеса 2 отложим абсолютную скорость точки К2, равную
, и перпендикулярно радиусу R2 в сторону вращения колеса 2 отложим абсолютную скорость точки К2, равную 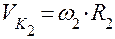 . Отметим угол β1 между радиусом R1 и перпендикуляром O1N1 к линии зацепления и β2 между радиусом R2 и перпендикуляром О2N2 также к линии зацепления. Спроецируем скорости
. Отметим угол β1 между радиусом R1 и перпендикуляром O1N1 к линии зацепления и β2 между радиусом R2 и перпендикуляром О2N2 также к линии зацепления. Спроецируем скорости 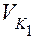 и
и 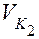 на линию зацепления N1N2. Линия зацепления направлена по нормали к профилям зубьев, поэтому проекции скоростей на неё являются нормальными составляющими, равными друг другу. Составляющие, направленные перпендикулярно линии зацепления, действуют по касательной к профилям и являются тангенциальными составляющими. Они определяются следующими цепоч-
на линию зацепления N1N2. Линия зацепления направлена по нормали к профилям зубьев, поэтому проекции скоростей на неё являются нормальными составляющими, равными друг другу. Составляющие, направленные перпендикулярно линии зацепления, действуют по касательной к профилям и являются тангенциальными составляющими. Они определяются следующими цепоч-
ками преобразований
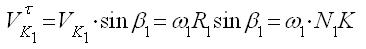
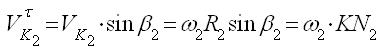
 C учётом этого ранее записанные выражения примут следующий вид:
C учётом этого ранее записанные выражения примут следующий вид:
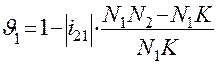 ,
, 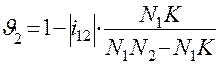 .
.
В этих выражениях буквой К обозначены совпадающие друг с другом точки К1 и К2. Схематический график удельного скольжения показан на рис. 3.15.
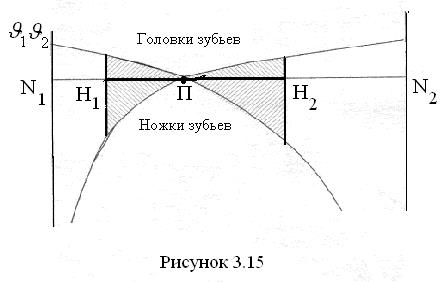 График показывает, что удельное скольжение на головках зубьев меньше чем на ножках, следовательно, ножки изнашиваются интенсивнее, чем головки. Характер износа таков, что чем дальше от полюса в радиальном направлении находится зона профиля, тем больше она изнашивается. В полюсе зацепления износ от скольжения равен нулю, так как эта точка является мгновенным центром поворота одного колеса относительно другого, и точки профилей, попадающие в полюс, имеют радиус относительного вращения вокруг полюса, равный нулю.
График показывает, что удельное скольжение на головках зубьев меньше чем на ножках, следовательно, ножки изнашиваются интенсивнее, чем головки. Характер износа таков, что чем дальше от полюса в радиальном направлении находится зона профиля, тем больше она изнашивается. В полюсе зацепления износ от скольжения равен нулю, так как эта точка является мгновенным центром поворота одного колеса относительно другого, и точки профилей, попадающие в полюс, имеют радиус относительного вращения вокруг полюса, равный нулю.
