Каковы закономерности знаковых систем, представляющих интеллектуальную продукцию в текстовой форме?

Ответ на этот вопрос не возможен без анализа современного научного направления, синтезированного исследованиями психологии, лингвистики, математики, физики информационных процессов и др. Остановимся кратко на избранных достижениях исследований языковых текстов.

В первой половине XX столетия исследования Эсту, Кондона и Ципфа завершились открытием статистического рангового распределения элементов словаря.

В чём суть этого открытия? Известно, что одни слова, как знаковые единицы, употребляются чаще, чем другие. Упорядочим их так: в качестве номера слова возьмём частоту n вхождения этого слова в тексты. Эту частоту назовём рангом, так что самое частое слово имеет ранг 1, второе по частоте слово имеет ранг 2 и т. д. Пусть P_n обозначает случайную частоту появления в тексте слова с рангом n. Тогда существует статистическое распределение, выражающее функциональную зависимость частоты P_n от ранга n. Бенуа Мандельброт объявил ранговое распределение законом языка. Этот закон представляется аналитической зависимостью [2], [12]:

P 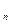= k/(b+n) ,

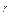где «гамма» приблизительно равна 1, постоянные величины k и b выражаются через частоту вхождения самого частого слова и длину текста.

Компьютерная обработка текстов показала, что закон Мандельброта не выражает математическое ожидание, к которому, по вероятности, сходятся ранговые распределения слов длинных текстов. То есть не выполняется статистический закон больших чисел. Более того, на разных текстовых выборках слова не сохраняют вероятности вхождения. Таким образом, гипотеза Мандельброта о законе языка в форме рангового распределения не подтвердилась.

В семидесятые годы советский кибернетик Ю. Орлов предположил, что закон Мандельброта справедлив для завершённых текстов [2]. Тем самым поставлена задача исследования закономерностей целостного восприятия текстов различной природы: художественных, музыкальных, специализированных. Фактически, это подводит нас к проблеме моделирования смысловых отношений в знаковых системах, представляющих тексты.

В историческом плане работа в этом направлении только начинается. Впереди – открытия, которые помогут нам осознать закономерности функционирования интеллектуальных систем посредством изучения текстовых структур – основного интеллектуального продукта. С современным состоянием исследований в этом направлении модно познакомиться по трудам научных конференций, см. например [2], [3], [12], а также указанную там библиографию.

Данное учебное пособие выполняет скромные функции семестрового курса математики, читаемого автором на гуманитарном факультете НГТУ. Целью курса является первое знакомство с идеями и методами математического формализма, т. е. математического языка. Автор считает, что математические тексты и структуры в определённом смысле являются образцами, представляющими простейшие интеллектуальные продукты. Насколько значительна роль математических стереотипов в исследовании общих текстовых структур автору неизвестно. Очевидно лишь то, что рождение новых информационных технологий и автоматизация интеллектуального труда требует ревизии многих сложившихся формализаций в науке, и соответствующие исследования лежат в пересечении гуманитарных и точных наук.

Мы будем знакомиться с математикой, как с искусственным языком и рассматривать ее в качестве интеллектуального ремесла. Поэтому главная наша задача состоит в том, чтобы понять назначение этого ремесла. Мы считаем, что смысл математического языка заключается в знаковой формализации канонических образов, которыми оперирует интеллект в различных информационных областях. Под знаковой формализацией образов мы понимаем направленное или волевое действие трех функций языка:

- присваивание мыслительному образу знака (действие опорной функции);

- оперирование образами как знаками (действие логической функции);

- реализация мысли в виде системы знаков (коммуникационная функция).

В указанном языковом смысле математику следует считать искусственной составляющей естественного интеллекта, развиваемой самим интеллектом для оптимизации своей деятельности.

Будем, например, считать одной из целей развития информационных технологий автоматизацию интеллектуального труда. Тогда мы с необходимостью признаем, что возможность компьютерного оперирования «образами» связано с преобразованием образов человеческих мыслей на язык отношений в определенных математических структурах. Поэтому, для начала, необходимо ответить на следующие вопросы:

- Как возникают математические структуры и что это такое?

- Как устроены такие структуры и как они функционируют?

Изучению этих вопросов мы посвящаем первую и вторую главы, названных нами, соответственно, «математический формализм» и «свойства аксиоматических систем».

“Господь Бог создал натуральные числа; все остальное дело рук человеческих”.

Леопольд Кронекер (1823-1891)

ГЛАВА I