Создание математической модели
ВВЕДЕНИЕ
Развитие машиностроительной индустрии, определяется уровнем совершенствования автоматизированного технологического оборудования (АТО). Повышение требований к быстродействию и точности их функционирования обусловливают необходимость совершенствования действующих и создания новых позиционных систем. Применение позиционных гидроприводов, в силу известных преимуществ позволяет повысить эффективность таких систем.
В позиционных гидросистемах программного регулирования, широкое применение нашли гидромеханические позиционеры - устройства организующие контур гидравлического управления. Они эффективно решают задачи оптимального управления выходного звена привода, используя гидравлические линии связи (ГЛС), позволяющие регулировать потоки жидкости на входе или выходе из гидродвигателя.
В результате схемотехнического поиска разработана модульная гидромеханическая система, обладающая возможностью эффективного структурно-параметрического управления процессами позиционирования целевых механизмов машин.
Структурная схема, показывающая взаимодействие ее силовой, гидравлической и механической подсистем, приведена на рисунке 1.
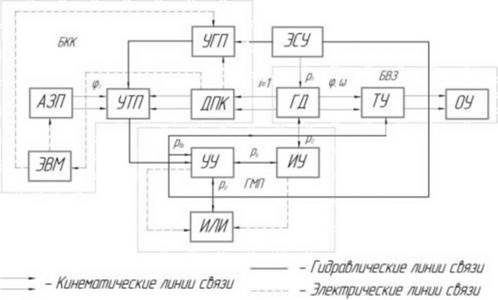
Рисунок 1 - Структурная схема позиционного гидропривода с ГЛС: АЗП - автоматический задатчик перемещений; ЭВМ - электронно-вычислительный модуль; ДПК - датчик положения координаты; УГП - устройство грубого перемещения; УТП - устройство точного перемещения; УУ - устройство управления; ИЛИ - логический элемент «или»; ЭСУ - энергосиловая установка; ГД - гидродвигатель; ИУ - исполнительное устройство; ТУ - тормозное устройство; ОУ - объект управления.
Гидравлическую подсистему образуют: энергосиловая установка (ЭСУ), гидродвигатель (ГД) и тормозное устройство. ЭСУ формирует требуемые параметры потока рабочей жидкости p1,p2,Q1,Q2 и преобразует его энергию в движение выходного звена ГД с заданными скоростью ю1 и крутящим моментом МГМ.
Отработку требуемого алгоритма позиционного цикла обеспечивает блок контроля координаты (БКК). Его реализуют: датчик положения координаты (ДПК), кинематически связанный с гидродвигателем. Срабатывание ДПК и передача сигнала на устройство грубого перемещения (УГП) формирующего управляющие воздействие ру происходит в точке позиционирования, задаваемой автоматическим задатчиком перемещений АЗП [5].
Гидравлический сигнал на выходе УГП формируется за 0,001...0,003 с давлением для прямого управления гидромеханическим позиционером (ГМП) встроенным в гидравлическую силовую систему и управляющих основными потоком гидродвигателя. Передачу сигналов осуществляют управляющие гидролинии связи (УГЛС). ГМП образуют: устройство управления (УУ) преобразующее и направляющее управляющий сигнал к исполнительному устройству (ИУ) регулирующему противодавление на сливе ГМ.
Особенностью гидравлических связей ГМП, являются незначительные расходы управляющих потоков в УГЛС, что позволяет минимизировать объемы жидкости в контуре и повысить его быстродействие управляющего устройства (ГМП). Объединение нескольких исполнительных устройств в одно многофункциональное, так же повышает быстродействие и стабильность работы системы.
Возможности дальнейших исследований функционала предлагаемого схемотехнического решения ПГП, во многом зависят от качественного математического описания его гидромеханической системы.
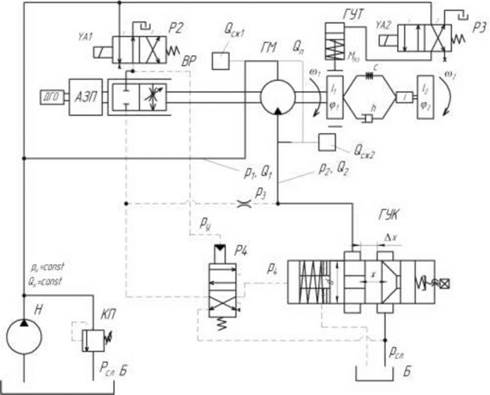
Рисунок 2 - Расчетная схема динамической системы ПГП
При этом существенно сокращается время последующих испытаний и улучшается качество рабочих процессов реальных ПГП, сокращая затраты времени и средств. Для этого был выполнен динамический анализ позиционного гидропривода в соответствии с ниже приведенной методикой.
Для этого, на основании структурной и принципиальной гидравлических схем, разработана расчетная гидрокинематическая схема динамической системы ПГП представленная на рисунке 2.
СОЗДАНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
Математическое описание динамических процессов протекающих в гидравлических системах осложняется особенностями поведением потока рабочей жидкости. Поэтому при формировании математической модели позиционной гидросистемы, были приняты следующие допущения в порядке их значимости:
· Механическую подсистему ГМУП в упрощённых моделях описывает одномассовая динамическая система, а в полной модели - двухмассовая;
· Утечки малы и могут быть ограничены коэффициентом утечки Ку [3];
· Трубопроводы короткие, гладкие, жесткие, что позволяет не учитывать волновые явления;
· Жесткость гидравлического силового контура Сг ниже жесткости механической подсистемы См;
· Динамические процессы протекают в окрестности точки нагрузочной характеристики привода: QН=const , рн=рклтах= const;
· Рабочая жидкость сжимаемая, капельная, в каналах присутствует нерастворённый воздух. Полагаем, что состояние среды описывается зависимостями, справедливыми для смесей с осреднёнными свойствами. Сосредоточенный объём сжимаемой жидкости <Зсж для удобства расчётов считаем присоединенным к рабочей полости гидродвигателя;
· Принимается, что сила вязкого трения в подвижных сопряжениях пропорциональна скорости, поскольку постоянная времени гидродинамического всплытия элемента больше времени переходного режима, то можно полагать, что сила трения пропорциональна скорости;
· Совмещение рабочих окон вращающегося распределителя происходит мгновенно при релейном управлении и по экспоненциальному закону - при квазирелейном управлении;
· Коэффициент расхода управляющего устройства ГУКа представлен аппроксимированной функциональной зависимостью от степени открытия золотника клапана µ=f(x) полученной экспериментально [5].
Используя основные принципы и правила математического описания динамических подсистем с механическими связями, обоснованных работами В.А. Кудинова, А.С. Проникова, В.Э. Пуша и др. [1], гидравлических силовых и управляющих подсистем, подтвержденных исследованиями О.Н. Трифонова, Д.Н. Попова и др. [3], составлена математическая модель, представляющая систему нелинейных дифференциальных уравнений, описывающих поведение ее подсистем.
1. Уравнения движения двухмассовой механической подсистемы:
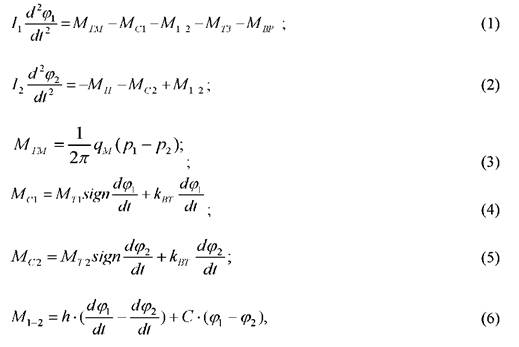


2. Гидравлическая силовая подсистема с дроссельным управлением описывается уравнениями баланса расходов характеризующими напорную и сливную линии:
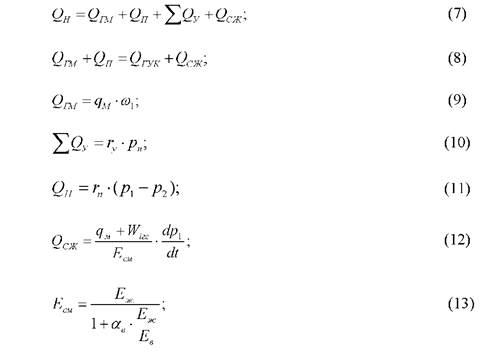

Зависимость дросселирования расхода рабочей жидкости Q3 через окна золотников гидрораспределителей, от изменения их проходного сечения и перемещения золотника Хр при перепаде давлений Ар определяется с помощью выражения:
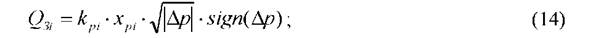

Преобразуя уравнения (7), (8) и выполнив подстановку значений расходов, получим уравнения характеризующие изменения давлений для напорной и сливной гидролиний:

3.Управляющая подсистема реализуется контуром гидравлического управления КГУ, описываемым подмоделями ВР, движением золотника ГУКа и управляющими гидролиниями.
а) Уравнение движения золотника распределителя Р4, управляющего ГУК:


б) Уравнение движения золотника гидроуправляемого клапана: 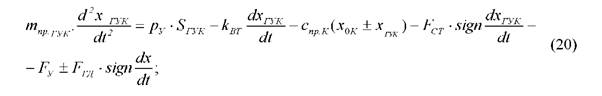

в) Уравнение управляющего давления распределителя Р4:
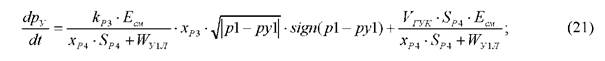

Математическая модель системы ПГП исследовалась с использованием программного пакета Matlab 2011a и её подсистемы модульного моделирования динамических процессов simulink. При решении, применяли прямой численный метод Рунге-Кутта и Эйлера с постоянным шагом интегрирования равным 0,00001. При этом принятые начальные условия, параметры контура гидравлического управления (Таблица 1) и управляющие воздействия (хг), имели функциональную зависимость от координаты выходного звена (<р )
