Среднее квадратическое отклонение

Определение. Средним квадратическим отклонениемслучайной величины Х называется квадратный корень из дисперсии.

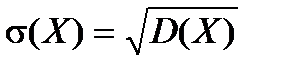
Теорема. Среднее квадратичное отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин.

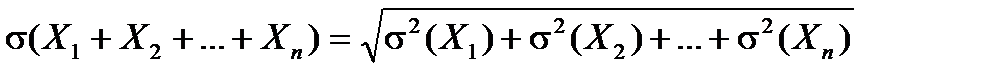
1. Для рассмотренного выше примера закон распределения случайной величины имеет вид:

X
p	0,0625	0,375	0,5625

Найти математическое ожидание и дисперсию случайной величины.

Решение.Математическое ожидание случайной величины равно:

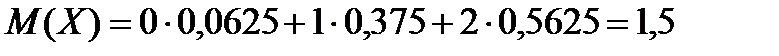
Возможные значения квадрата отклонения:

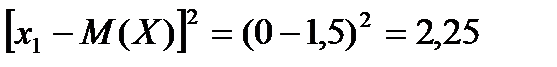
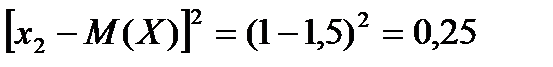
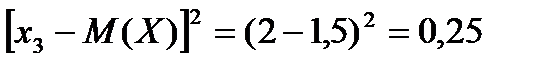
Тогда

[X-M(X)]2	2,25	0,25	0,25
p	0,0625	0,375	0,5625

Дисперсия равна:

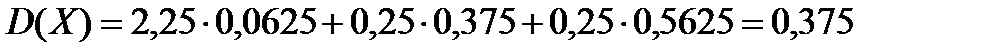
Однако, на практике подобный способ вычисления дисперсии неудобен, т.к. приводит при большом количестве значений случайной величины к громоздким вычислениям.

Поэтому применяется другой способ.

Применим эту формулу для рассмотренного выше примера:

X
X2
p	0,0625	0,375	0,5625

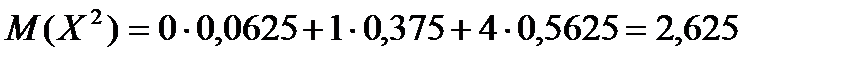
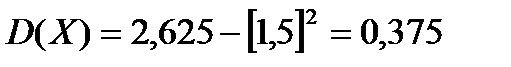
1. Завод выпускает 96% изделий первого сорта и 4% изделий второго сорта. Наугад выбирают 1000 изделий. Пусть Х – число изделий первого сорта в данной выборке. Найти закон распределения, математическое ожидание и дисперсию случайной величины Х.

Решение.Выбор каждого из 1000 изделий можно считать независимым испытанием, в котором вероятность появления изделия первого сорта одинакова и равна р = 0,96.

Таким образом, закон распределения может считаться биноминальным.

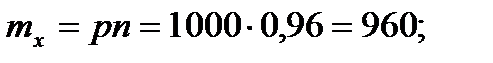
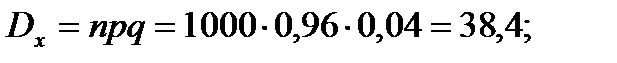
Контрольные вопросы:

1. Определения событий и вероятности.

2. Формулы для вычисления вероятности

3. Формулы суммы вероятностей совместных и несовместных событий.

4. Формулы произведения вероятностей зависимых и независимых событий.

5. Понятие случайной величины.

6. Закон распределения дискретной случайной величины.

7.Математическое ожидание и дисперсия дискретной случайной величины.

Литература.

1. М.И. Башмаков. «Алгебра и начала анализа 10-11 кл» (М., Просвещение, 1991г)

2. Н.Я.Виленкин, О.С.Ивашев-Мусатов, С.И. Шварцбурд. « Алгебра и начала анализа, 11кл» (М., Просвещение, 1992г)

3. В.М. Клопский, З.А.Скопец, М.И. Ягодовский «Геометрия 9-10 кл»

4. Л.С. Атанасян, В.Ф.Бутузов «Геометрия 10-11 кл»

5. Гусев А., Қагазбаева,... Геометрия 10 кл.

6. Математика для техникумов. Алгебра и начало анализа. (под. ред. Г.Н. Яковлева. I часть М. 1987г).

7. Математика для техникумов. Алгебра и начало анализа.(под. ред. Г.Н. Яковлева. II часть М. 1988г).

8. Математика для техникумов. Геометрия.(под. ред. Г.Н. Яковлева. М. 1987г).

9. Апанасов П.Т., Орлов М.И. Сборник задач по математике. М. 1987г.