Центральное растяжение (сжатие) прямого бруса. Расчёты на прочность и жёсткость. Условие прочности. Условие жёсткости. Три типа задач при расчёте на прочность
Центральное напряжение (сж.) прямого бруса см. в вопросе 8.
max|σz|растяж≤[σ]растяж; max|σz|сжатия≤[σ]сжатия.
Обобщённый закон Гука для трёхосного напряжённого состояния в точке. Относительная объёмная деформация. Коэффициент Пуассона и его предельные значения для однородного изотропного материала.
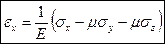 ,
, 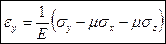 ,
, 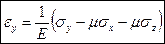 . Сложив эти уравнения, получим выражение объёмной деформации:
. Сложив эти уравнения, получим выражение объёмной деформации: 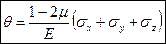 . Это выражение позволяет определить предельное значение коэффициента Пуассона для любого изотропного материала. Рассмотрим случай, когда σx=σy=σz=р. В этом случае:
. Это выражение позволяет определить предельное значение коэффициента Пуассона для любого изотропного материала. Рассмотрим случай, когда σx=σy=σz=р. В этом случае: 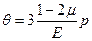 . При положительном р величина θ должна быть также положительной, при отрицательном р изменение объёма будет отрицательным. Это возможно только в том случае, когда μ≤1/2. Следовательно, значение коэффициента Пуассона для изотропного материала не может превышать 0,5.
. При положительном р величина θ должна быть также положительной, при отрицательном р изменение объёма будет отрицательным. Это возможно только в том случае, когда μ≤1/2. Следовательно, значение коэффициента Пуассона для изотропного материала не может превышать 0,5.
Соотношение между тремя упругими постоянными для изотропного материала (без вывода формулы).
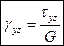 ,
, 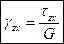 ,
, 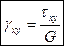 .
.
Исследование напряжённо-деформированного состояния в точках центрально-растянутого (сжатого) прямого бруса. Закон парности касательных напряжений.
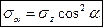 ,
, 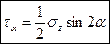 .
.
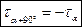 - закон парности касательных напряжений.
- закон парности касательных напряжений.
Центральное растяжение (сжатие) бруса из линейно-упругого материала. Потенциальная энергия упругой деформации бруса и её связь с работой внешних продольных сил, приложенных к брусу.
А=U+K. (В результате работы накапливается потенциальная энергия деформированного тела U, кроме того, работа идёт на совершение скорости массе тела, т.е. преобразуется в кинетическую энергию).
Если центральное растяжение (сжатие) бруса из линейно-упругого материала производится очень медленно, то скорость перемещения центра масс тела будет весьма малой. Такой процесс нагружения называется статическим. Тело в любой момент находится в состоянии равновесия. В этом случае А=U, и работа внешних сил целиком преобразуется в потенциальную энергию деформации. 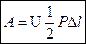 ,
, 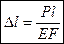 ,
, 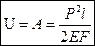 .
.
Удельная потенциальная энергия линейно-упругого материала при одноосном напряжённом состоянии и при чистом сдвиге.
Удельная потенциальная энергия линейно-упругого материала при одноосном напряжённом состоянии 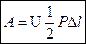 ,
, 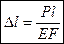 ,
, 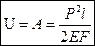 .
.
Чистый сдвиг – такое напряжённое состояние, когда на гранях выделенного элемента возникают только касательные напряжения τ.
Удельная потенциальная энергия линейно-упругого материала при чистом сдвиге: 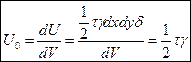 , где δ – толщина пластины, τ – касательные напряжения, γ – угловая деформация. По закону Гука:
, где δ – толщина пластины, τ – касательные напряжения, γ – угловая деформация. По закону Гука: 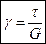 =>
=> 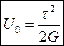 .
.
Поперечный изгиб прямого бруса. Определение внутренних усилий в поперечных сечениях бруса методом сечений. Правила знаков для внутренних усилий. Привести числовые примеры определения внутренних усилий.
Поперечный изгиб – такой изгиб, при котором в поперечных сечениях бруса помимо изгибающего момента (например, Мх) возникает и поперечная сила Qy.
Если сумма поперечных сил, действующих на левую часть бруса, положительная, то ордината силы Qy в сечении откладывается вверх. Если же равнодействующая поперечная сила слева от сечения даёт отрицательный результат, то ордината силы Qy откладывается вниз.
Если сумма моментов сил, действующих на левую часть бруса, даёт равнодействующий момент, направленный по часовой стрелке, то ордината изгибающего момента в сечении откладывается вверх. Если же равнодействующий внешний момент слева от сечения направлен против хода часовой стрелки, то ордината изгибающего момента откладывается вниз.
