Определение непрерывности в точке
Функция 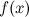 называется непрерывной в точке
называется непрерывной в точке  , если:
, если:
1. функция 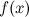 определена в точке
определена в точке  и ее окрестности;
и ее окрестности;
2. существует конечный предел функции 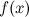 в точке
в точке  ;
;
3. это предел равен значению функции в точке  , т.е.
, т.е. 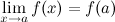
При нахождении предела функции 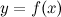 , которая является непрерывной, можно переходить к пределу под знаком функции, то есть
, которая является непрерывной, можно переходить к пределу под знаком функции, то есть 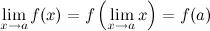
Пусть функция 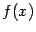 определена на некотором интервале
определена на некотором интервале 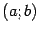 , для которого
, для которого 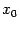 -- внутренняя точка. Функция
-- внутренняя точка. Функция 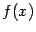 называется непрерывной в точке
называется непрерывной в точке 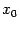 , если существует предел
, если существует предел 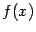 при
при 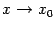 и этот предел равен значению
и этот предел равен значению 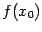 , то есть
, то есть 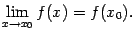 Пусть функция
Пусть функция 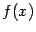 определена на некотором полуинтервале
определена на некотором полуинтервале 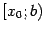 , для которого
, для которого 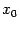 -- левый конец. Функция
-- левый конец. Функция 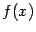 называется непрерывной справа в точке
называется непрерывной справа в точке 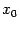 , если существует предел
, если существует предел 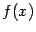 при
при 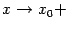 и этот предел равен значению
и этот предел равен значению 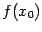 , то есть
, то есть 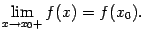 Пусть, наконец, функция
Пусть, наконец, функция 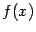 определена на некотором полуинтервале
определена на некотором полуинтервале 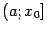 , для которого
, для которого 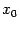 -- правый конец. Функция
-- правый конец. Функция 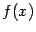 называется непрерывной слева в точке
называется непрерывной слева в точке 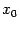 , если существует предел
, если существует предел 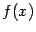 при
при 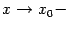 и этот предел равен значению
и этот предел равен значению 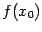 , то есть
, то есть
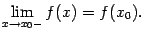
Из теоремы о связи двустороннего предела с односторонними (теорема 2.1) сразу следует, как уже отмечалось в главе 2, что имеет место следующее предложение.
Функция 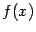 тогда и только тогда непрерывна в точке
тогда и только тогда непрерывна в точке 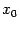 , когда она непрерывна в точке
, когда она непрерывна в точке 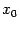 справа и слева, то есть когда выполнены следующие условия:
справа и слева, то есть когда выполнены следующие условия:
1) функция 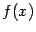 определена в точке
определена в точке 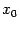 и в некоторой окрестности этой точки;
и в некоторой окрестности этой точки;
2) существует предел значений функции слева: 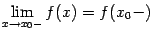 ;
;
3) существует предел значений функции справа: 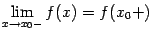 ;
;
4) эти два предела совпадают между собой и со значением функции в точке 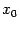 :
: 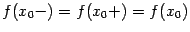 .
.
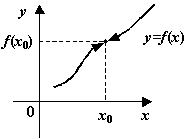
Рис.3.1.Функция непрерывна: пределы слева и справа совпадают с 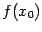
Точка 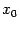 , в которой функция непрерывна, называется точкой непрерывности функции
, в которой функция непрерывна, называется точкой непрерывности функции 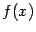 ; так же определяются точки непрерывности слева и справа.
; так же определяются точки непрерывности слева и справа.
Свойства непрерывных функций на отрезке
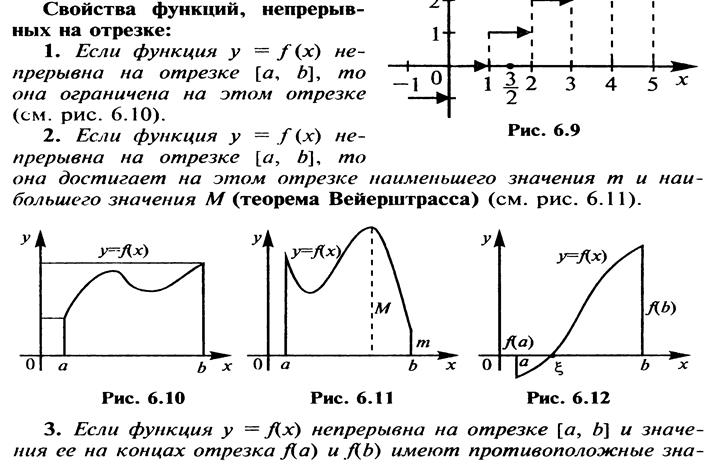
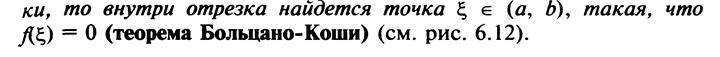
Классификация точек разрыва
Устранимый разрыв.
Он имеет место, когда выполнено условие
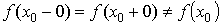 .
.
В данном случае достаточно изменить значение функции в точке x0, чтобы разрыва не стало.

Рис. 2.1 Вид устранимого разрыва
Разрыв первого рода (скачок).
Разрыв первого рода (скачок) получается тогда, когда односторонние пределы 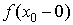 и
и 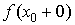 существуют, конечны, но не равны между собой,то есть
существуют, конечны, но не равны между собой,то есть 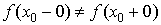 .
.
Вид функции в случае разрыва первого рода приведен на рис. 2.2.

Рис. 2.2 Вид разрыва первого рода.
Разрыв второго рода.
Если хотя бы один из 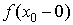 и
и 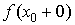 равен ¥± или не существует, то говорят, что функция f(x) имеет в точке x0 разрыв второго рода.
равен ¥± или не существует, то говорят, что функция f(x) имеет в точке x0 разрыв второго рода.
Вид разрывов второго рода очень разнообразен. Пример такого разрыва приведен на рис. 2.3. На нем изображен случай, когда f(x0 – 0) конечен, а f(x0 + 0) равен +¥.
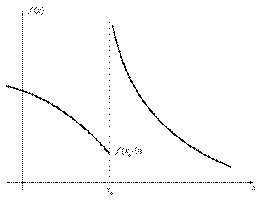
Рис. 2.3. Пример разрыва второго рода.
