Свойства математического ожидания

ЛЕКЦИЯ 4_5: «СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ»

Дискретные и непрерывные случайные величины

Определение 1. Случайной величиной называют переменную величину, которая в зависимости от исхода испытания случайно принимает одно значение из множества возможных значений.

Пример. Число очков, выпавших при однократном бросании игральной кости, есть случайная величина, она может принять одно из значений 1, 2, 3, 4, 5, 6.

Случайные величины обозначаются прописными буквами X, Y, Z, а их возможные значения – соответствующими строчными буквами x, y, z.

Определение 2. Случайная величина, принимающая различные значения, которые можно записать в виде конечной или бесконечной последовательности, называется дискретнойслучайной величиной.

Определение 3. Случайная величина, которая может принимать все значения из некоторого числового промежутка, называется непрерывной случайной величиной.

Законы распределения дискретных случайных величин

Дискретная величина X считается заданной, если перечислены все её возможные значения, а также вероятности, с которыми величина X может принять эти значения. Указанный перечень возможных значений и их вероятностей называют законом распределения дискретной случайной величины. Обычно он задаётся с помощью таблицы:

X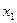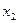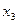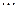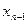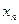
p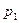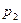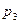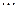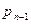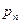

Так как в результате испытания величина X всегда примет одно из значений 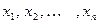, то .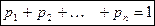

Пример. Пусть случайная величина X – число очков, выпавших при бросании игральной кости. Найти закон распределения случайной величины X.

X
p	1/6	1/6	1/6	1/6	1/6	1/6

Математическое ожидание и дисперсия дискретной случайной величины

Определение 1. Математическим ожиданием дискретной случайной величины называется сумма произведений значений случайной величины на вероятности этих значений.

Если случайная величина характеризуется конечным рядом распределения

X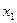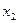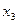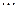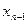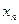
p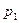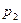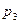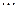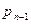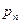

то математическое ожидание 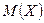определяется по формуле

.

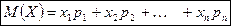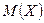является взвешенным средним арифметическим значений случайной величины 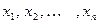при весах .

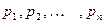Пример. Найти математическое ожидание случайной величины X, зная закон её распределения.

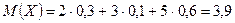
X
p	0,3	0,1	0,6

Свойства математического ожидания.

1.

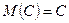
2.

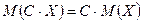
3.

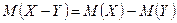
4.

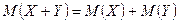
5.

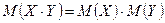
Пример. Независимые случайные величины X и Y заданы следующими законами распределения:

X
p	0,1	0,3	0,6

Y
p	0,8	0,2

Найти математическое ожидание случайной величины XY.

,

,

.

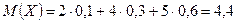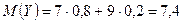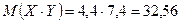Определение 2. Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

.

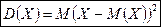Пример. Найти дисперсию случайной величины X, которая задана следующим законом распределения:

X
p	0,3	0,5	0,2

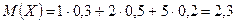
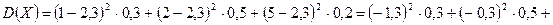
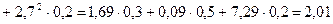
Дисперсия случайной величины есть мера рассеяния её значений около её математического ожидания.

Свойства дисперсии.

1.

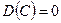
2.

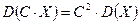
3.

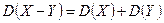
4.

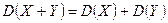
Определение 3. Средним квадратическим отклонением 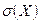случайной величины X называется корень квадратный из её дисперсии:

.

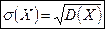Пример. Случайная величина X – число очков, выпавших при однократном бросании игральной кости. Определить .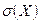

Закон распределения случайной величины X задан таблицей:

X
p	1/6	1/6	1/6	1/6	1/6	1/6

Находим математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X:

;

;

.

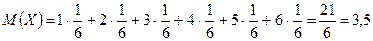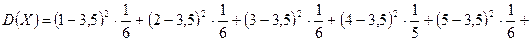
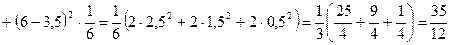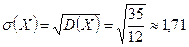Введение среднего квадратического отклонения объясняется тем, что дисперсия измеряется в квадратных единицах относительно размерности самой случайной величины. В тех случаях, когда нужно иметь числовую характеристику рассеяния возможных значений в той же размерности, что и сама случайная величина, используется среднее квадратическое отклонение.

Задачи

1. Найти дисперсию и среднее квадратическое отклонение дискретной случайной величины X, заданной законом распределения:

X	-5
p	0,4	0,3	0,1	0,2

2. Найти дисперсию и среднее квадратическое отклонение дискретной случайной величины X, заданной законом распределения:

X	4,3	5,1	10,6
p	0,2	0,3	0,5