Рациональное сечение сжатой стойки
При продольном изгибе
Стойка из стального прокатного двутавра, сжата силой F (рис. 1) и имеет заданную расчётную схему
Требуется:
1.Заменить заданное сечение составным сечением из двух элементов (рис. 2) с общей площадью, не превышающей площадь двутавра.
2.Определить грузоподъёмность стойки в обоих вариантах.
3.Сравнить допускаемые нагрузки и сделать вывод о более рациональном сечении сжатой стойки.
Расчётная схемаИсходные данные

| Шифр | Номер двутавра | l м | R МПа | гc |
| 31-6 | 3,1 | 0,95 |
Решение
Заданная стойка изготовлена из двутавра № 30 с геометрическими характеристиками
A = 46,5 см2, ix = 12,3 см, iy = 2,69 см.
Из этих данных можно заключить, что двутавр является нерациональной формой сечения при продольном нагружении стойки с возможной потерей устойчивости. Его материал распределён так, что один из радиусов инерции (iy) значительно меньше другого. В двух плоскостях хОz и yOz критические силы будут существенно различаться, т.е. стойка не является равноустойчивой в указанных плоскостях, что ведёт к недоиспользованию прочностных свойств материала. По этим причинам предлагается перераспределить материал, не увеличивая площади сечения (значит, не увеличивая расхода), на два элемента: стандартный швеллер и стальную полосу. Толщина полосы задана, второй размер выберем таким образом, чтобы осевые моменты сечения впоследствии оказались примерно одинаковыми, т.е. Jx  Jy. Примем его равным 19 см. Её площадь сечения легко вычисляется
Jy. Примем его равным 19 см. Её площадь сечения легко вычисляется
А1 = 19·1 = 19 см2.
По условию задачи
А2 ≤ А – А1 =46,5 – 19 = 27,5 см2.
Из сортамента берём швеллер № 22 с площадью сечения
А2 = 26,7 см2.
Составное сечение с необходимыми размерами в более крупном масштабе показано на рис. 2. Здесь x0, y0 – координатные оси, относительно которых будут отыскиваться координаты центра тяжести. Ось х-ов совпадает с осью
 |
симметрии сечения и потому является одной из главных центральных осей. Остальные обозначенные оси являются собственными осями элементов сечения. Два варианта стойки будем сравнивать по их грузоподъёмности, т.е. по величине допускаемых нагрузок. Перейдём к их определению.
Допускаемое значение силы должно удовлетворять условию устойчивости
у = 
Отсюда
F = [F] =  R γc A. (1)
R γc A. (1)
Рассмотрим оба варианта.
1.Двутавр. Коэффициент приведения длины определяется в зависимости от условий закрепления концов стержня и равен
µ = 1.
Коэффициент продольного изгиба ц зависит от гибкости

| R=200 МПа | |
| λ | 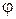 |
| 0,537 | |
| 0,479 |
Приведён фрагмент таблицы для коэффициента продольного изгиба стали при R= 200 МПа. Отсюда по линейной интерполяции для гибкости 115,2 получим

Подставим в (1) и вычислим
[F]2 = 0,507·200·106·0,95·46,5·10-4 = 474439 Н = 474,4 кН. (2)
2.Составное сечение. В этом случае потребуется подробное вычисление геометрических характеристик. Сначала рассмотрим каждый элемент отдельно.
Полоса.
А1 = 19 см2, х1 =19/2=9,5 см,
J  =
= 
 .
.
Швеллер №24. Из таблицы: «Швеллеры стальные горячекатаные (ГОСТ 8240 – 89)» возьмём данные
А2 = 26,7 см2, х2 = -2,21 см, J  = 2110 см4, J
= 2110 см4, J  = 151 см4,
= 151 см4,
Вычислим геометрические характеристики составного сечения.
Площадь
A = A1 + А2 = 19 + 26,7 ·= 45,7 см2.
Координата центра тяжести

Расстояние между параллельными осями y и y1, y и y2
a1 = хС - х1= 2,66 – 9,5 = -6,84 см, a2 = хС - х2= 2,66 +2,21 = 4,87 см.
Осевые моменты инерции
Jx = J  + J
+ J  = 1,58 + 2110 = 2112 см4,
= 1,58 + 2110 = 2112 см4,

Моменты инерции оказались примерно одинаковыми, поэтому ранее назначенный размер полосы 19 см корректировать не будем. В противном случае пришлось бы его уточнять, пытаясь добиться примерного равенства осевых моментов инерции. При этом, естественно, были бы повторены все предыдущие вычисления.
Радиусы инерции
ix =  см, iy =
см, iy =  см.
см.
Полученные радиусы инерции имеют близкие значения, из чего следует, что это сечение будет примерно равноустойчивым по отношению к осям x и у. Минимальный радиус инерции
imin = ix= 6,8 см
значительно превосходит радиус инерции двутавра, что приведёт к существенному увеличению грузоподъёмности стойки.
Определим гибкость стержня

Такой гибкости соответствует коэффициент продольного изгиба (см. фрагмент из таблицы ниже)
| R=200 МПа | |
| λ | 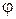 |
| 0,906 | |
| 0,869 |

Тогда допускаемая нагрузка по (1) имеет значение
 (3)
(3)
Разница в процентах между двумя значениями допускаемой нагрузки (2) и (3) большая и составляет в процентах

Данный результат показывает, что правильный выбор типа сечения, компоновка элементов составных сечений имеют существенное значение для повышения эффективности использования материала конструкции
Коэффициенты ц продольного изгиба центрально сжатых элементов
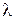 | 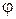 | 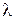 | 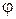 | ||
 , МПа , МПа |  , МПа , МПа | ||||
| 0,988 | 0,987 | 0,479 | 0,419 | ||
| 0,967 | 0,962 | 0,425 | 0,364 | ||
| 0,939 | 0,931 | 0,376 | 0,315 | ||
| 0,906 | 0,894 | 0,328 | 0,276 | ||
| 0,869 | 0,852 | 0,290 | 0,244 | ||
| 0,827 | 0,805 | 0,259 | 0,218 | ||
| 0,782 | 0,754 | 0,233 | 0,196 | ||
| 0,734 | 0,686 | 0,210 | 0,177 | ||
| 0,665 | 0,612 | 0,191 | 0,161 | ||
| 0,599 | 0,542 | 0,174 | 0,147 | ||
| 0,537 | 0,478 | 0,160 | 0,135 |
ВАРИАНТЫ ЗАДАНИЙ
| Второе число шифра | Номер двутавра | R МПа | γc |
| 0,90 | |||
| 0,95 | |||
| 0,95 | |||
| 0,90 | |||
| 0,95 |
Примечание: В заменяющих схемах 23-27 указан только один из размеров (1 см) стальной полосы. Второй размер подбирается студентом (см. пример, приведённый выше)
 |
Таблица 1
| Первое число шифра | Расчётная схема | l м | Заменяющее сечение |
| 3,0 | |||
| 2,6 | |||
| 2,5 | |||
| 3,1 | |||
| 3,4 | |||
| 4,0 | |||
| 3,1 | |||
| 2,8 | |||
| 2,7 | |||
| 3,2 | |||
| 3,6 | |||
| 4,2 | |||
| 3,0 | |||
| 2,7 | |||
| 2,4 | |||
| 3,0 | |||
| 3,5 | |||
| 3,9 | |||
| 2,9 | |||
| 2,4 | |||
| 2,7 | |||
| 2,8 | |||
| 3,7 | |||
| 4,3 | |||
| 3,3 | |||
| 2,9 | |||
| 2,8 | |||
| 2,9 | |||
| 3,3 | |||
| 4,1 |
 |
Литература
1. Александров А.В. Потапов В.Д. Державин Б.П. Сопротивление материалов. – М.: Высшая школа, 2000. – 560 с.
2. Андреев В.И., Паушкин А.Г., Леонтьев А.Н. Техническая механика (для учащихся строительных вузов и факультетов). Учебник. –М., Издательство АСВ, 2012 с.
3. Атаров Н.М., Варданян Г.С., Горшков А.А., Леонтьев А.Н.Сопротивление материалов. Учебное пособие. Ч. 1 / –М.: МГСУ, 2009. –64 с.
4. Атаров Н.М., Варданян Г.С., Горшков А.А., Леонтьев А.Н.Сопротивление материалов. Учебное пособие. Ч. 2 / –М.: МГСУ, 2010. –80 с.
5. Атаров Н.М., Варданян Г.С., Горшков А.А., Леонтьев А.Н.Сопротивление материалов. Учебное пособие. Ч. 3 / –М.: МГСУ, 2010. –73 с.
6. Атаров Н.М.Сопротивление материалов в примерах и задачах:Учебное пособие. –М.: ИНФРА-М, 2013. – 407 с.
7. Варданян Г.С. и др. Сопротивление материалов с основами теории упругости и пластичности. – М.: изд. Ассоц. строит. вузов, 1995. –572 с.
8. Варданян Г.С., Атаров Н.М., Горшков А.А.Сопротивление материалов (с основами строительной механики). Под. ред. Г.С.Варданяна. –М.: ИНФРА-М, 2011. –480 с.
9. Михайлов А.М. Сопротивление материалов: учебник для студентов высших учебных заведений / А.М. Михайлов.–М.: Издательский центр «Академия», 2009. – 448 с.
10. Саргсян А.Е. Сопротивление материалов, теории упругости и пластичности. – М., 2000. – 286 с.
11. Феодосьев В.И. Сопротивление материалов. – М.: Изд-во МГТУ, 1999. – 591 с.
12. Сайт кафедры теоретической и прикладной механики: http://kafedratpm.ucoz.ru.
Содержание
| Общие указания по выполнению заданий …………………………………… | |
| Примеры решений и варианты заданий…………………………….………… | |
| Задача 1. Внутренние силы в сечениях криволинейного стержня и расчёты на прочность……………………………………………….. | |
| Задача 2 Определение перемещений при изгибе плоской рамы …………… | |
| Задача 3. Прочность бруса при сложном сопротивлении ………………..…. | |
| Задача 4. Плоские статически неопределимые рамы……..…………………. | |
| Задача 5. Балки на упругом основании.………………………………………. | |
| Задача 6. Расчет балки методом конечных разностей……………….………. | |
| Задача 7. Рациональное сечение сжатой стойки при продольном изгибе….. | |
| Литература……………………………………………………………………… |
Учебное издание
Тилова Залина Аслановна
Алокова Мадина Хасановна
