Исследователь вносит гипотезу о структуре ящика
Рассматривая экспериментально полученные данные, предположим, что они подчиняются линейной гипотезе, то есть выход Y зависит от входа X линейно, то есть гипотеза имеет вид:  (рис. 5.2).
(рис. 5.2).
2) Определение неизвестных коэффициентов A0 и A1 модели
Линейная одномерная модель (рис. 5.3).

Рис. 5.3. Одномерная модель черного ящика
Для каждой из 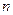 снятых экспериментально точек вычислим ошибку
снятых экспериментально точек вычислим ошибку  между экспериментальным значением
между экспериментальным значением  и теоретическим значением
и теоретическим значением  , лежащим на гипотетической прямой
, лежащим на гипотетической прямой  (см. рис. 5.2):
(см. рис. 5.2):


Ошибки  для всех
для всех 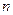 точек следует сложить. Чтобы положительные ошибки не компенсировали в сумме отрицательные, каждую из ошибок возводят в квадрат и складывают их значения в суммарную ошибку
точек следует сложить. Чтобы положительные ошибки не компенсировали в сумме отрицательные, каждую из ошибок возводят в квадрат и складывают их значения в суммарную ошибку  уже одного знака:
уже одного знака:


Цель метода — минимизация суммарной ошибки  за счет подбора коэффициентов
за счет подбора коэффициентов  . Другими словами, это означает, что необходимо найти такие коэффициенты
. Другими словами, это означает, что необходимо найти такие коэффициенты  линейной функции
линейной функции  , чтобы ее график проходил как можно ближе одновременно ко всем экспериментальным точкам. Поэтому данный метод называется методом наименьших квадратов.
, чтобы ее график проходил как можно ближе одновременно ко всем экспериментальным точкам. Поэтому данный метод называется методом наименьших квадратов.

Суммарная ошибка  является функцией двух переменных
является функцией двух переменных  и
и  , то есть
, то есть  , меняя которые, можно влиять на величину суммарной ошибки (см. рис. 5.4).
, меняя которые, можно влиять на величину суммарной ошибки (см. рис. 5.4).

Рис. 5.4. Примерный вид функции ошибки
Чтобы суммарную ошибку минимизировать, найдем частные производные от функции  по каждой переменной и приравняем их к нулю (условие экстремума):
по каждой переменной и приравняем их к нулю (условие экстремума):


После раскрытия скобок получим систему из двух линейных уравнений:


Для нахождения коэффициентов  и
и  методом Крамера представим систему в матричной форме:
методом Крамера представим систему в матричной форме:


Решение имеет вид:


Вычисляем значения  и
и  .
.
Проверка
Чтобы определить, принимается гипотеза или нет, нужно, во-первых, рассчитать ошибку между точками заданной экспериментальной и полученной теоретической зависимости и суммарную ошибку:


И, во-вторых, необходимо найти значение  по формуле
по формуле  , где
, где  — суммарная ошибка,
— суммарная ошибка, 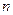 — общее число экспериментальных точек.
— общее число экспериментальных точек.
Если в полосу, ограниченную линиями  и
и  (рис. 5.5), попадает 68.26% и более экспериментальных точек
(рис. 5.5), попадает 68.26% и более экспериментальных точек  , то выдвинутая нами гипотеза принимается. В противном случае выбирают более сложную гипотезу или проверяют исходные данные. Если требуется большая уверенность в результате, то используют дополнительное условие: в полосу, ограниченную линиями
, то выдвинутая нами гипотеза принимается. В противном случае выбирают более сложную гипотезу или проверяют исходные данные. Если требуется большая уверенность в результате, то используют дополнительное условие: в полосу, ограниченную линиями  и
и  , должны попасть 95.44% и более экспериментальных точек
, должны попасть 95.44% и более экспериментальных точек  .
.

Рис. 5.5. Исследование допустимости принятия гипотезы
Расстояние  связано с
связано с  следующим соотношением:
следующим соотношением:

что проиллюстрировано на рис. 5.6.

Рис. 5.6. Связь значений σ и S
Условие принятия гипотезы выведено из нормального закона распределения случайных ошибок (см. рис. 5.7).  — вероятность распределения нормальной ошибки.
— вероятность распределения нормальной ошибки.

Рис. 5.7. Иллюстрация закона нормального распределения ошибок
