Лектор к.ф.-м.н., доцент Набебин А.А
Заведующий кафедрой ММ
Д.ф.-м.н., проф.
Амосов А.А.
ЭКЗАМЕНАЦИОННАЯ ПРОГРАММА
По курсу
МАТЕМАТИЧЕСКАЯ ЛОГИКА И ТЕОРИЯ АЛГОРИТМОВ
Поток А-4,6-8,12-2014, курс 2, АВТИ
Математическая логика
1. Множество, мощность, счетность, несчетность. Континуум. Теорема Кантора. Отношение эквивалентности.
2. Функции алгебры логики. Свойства булевых операций. Совершенная дизъюнктивная нормальная форма (СДНФ). Совершенная конъюнктивная нормальная форма (СКНФ). Двойственные функции. Принцип двойственности. Класс самодвойственных функций. Критерий самодвойственности. Лемма о несамодвойственной функции. Класс линейные функции. Полином Жегалкина. Лемма о нелинейной функции. Класс функций, сохраняющих константу. Монотонные функции. Лемма о немонотонной функции. Теорема Поста о функциональной полноте.
3. Формально аксиоматическое исчисление высказываний. Алфавит, формулы, интерпретация формул, система аксиом, правила вывода. Доказательство и доказуемая формула. Теорема дедукции. Производные правила вывода (силлогизм, снятие двойного отрицания, контрапозиции, перестановка посылок, соединение и разъединение посылок, введение конъюнкции и дизъюнкции, приведение к абсурду. Семантическая и синтаксическая полнота исчисления высказываний. Разрешимость и непротиворечивость.
4. Логика предикатов. Кванторы. Формулы. Интерпретация формул. Выполнимость, невыполнимость, общезначимость, опровержимость. Эквивалентность формул, эквивалентные преобразования. Нормальные формы: префиксная нормальная форма, стандартная форма Сколема. Проблема алгоритмической разрешимости формул логики предикатов.
5. Формально аксиоматическое исчисление предикатов. Алфавит, термы, формулы. Аксиоматика и правила вывода. Доказательство и доказуемые формулы. Непротиворечивость. Семантическая полнота. О синтаксической полноте. Аксиоматическая арифметика. Понятие о теоремах Геделя.
Теория алгоритмов
1. Арифметические функции. Подстановка, примитивная рекурсия, минимизация.
2. Примитивно рекурсивное описание. Примитивно рекурсивные функции. Примитивная рекурсивность относительно совокупности функций. Функции, представимые термом.
3. Конечные сумма и произведение.
4. Представляющая и характеристическая функции предиката. Примитивно рекурсивные предикаты.
5. Примеры примитивно рекурсивных функций и предикатов.
6. Ограниченные кванторы. Ограниченный оператор мю.
7. Подстановка функций в предикат. Кусочное задание функции.
8. Частично рекурсивные функции. Тезис Черча.
9. Машина Тьюринга. Вычисления на машинах Тьюринга.
10. Синтез машин Тьюринга. Композиция, ветвление, зацикливание машин Тьюринга.
11. Машины Тьюринга в однобуквенном алфавите.
12. Машины A,B,C,D,L, 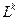 ,R,
,R, 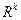 ,P,V,
,P,V, 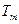 ,
, 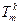 ,
, 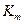 ,S.
,S.
13. Правильно вычислимые функции. Суперпозиция, примитивная рекурсия, минимизация правильно вычислимых функций. Правильная вычислимость частично рекурсивных функций.
14. Частичная рекурсивность правильно вычислимых функций. Геделева нумерация ситуаций машины Тьюринга. Функции программы машины Тьюринга. Функции вычисления по программе машины Тьюринга. Функции ситуаций машины Тьюринга. Теорема о частичной рекурсивности правильно вычислимых функциях. Представление Клини частично рекурсивной функции.
15. Универсальная частично рекурсивная функция. Геделева нумерация машин Тьюринга.
16. Проблема самоприменимости машины Тьюринга.
17. Теорема Клини о неподвижной точке и теорема Райса.
18. Рекурсивная перечислимость и разрешимость. Общерекурсивные функции и предикаты.
Лектор к.ф.-м.н., доцент Набебин А.А.
