Решение задачи Коши для ненагруженной ЭМС с нулевыми начальными условиями классическим способом

Найдем собственные значения матрицы А с помощью программы MathCAD:

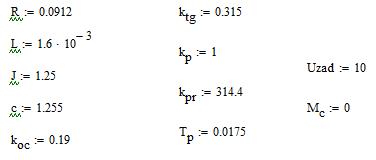
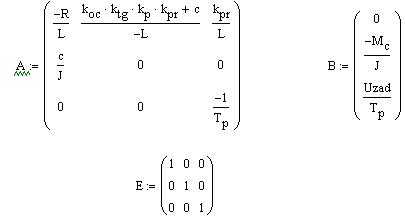
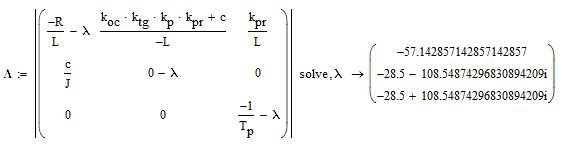
Собственные значения матрицы А совпали с определенными в программной среде MATLAB Simulink с небольшой погрешностью, обусловленной разной точностью расчетов программных продуктов.

Найдем собственные вектора матрицы А для каждого ее собственного значения из полученной системы уравнений, которую считаем однородной:

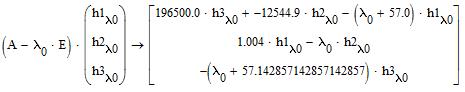
Определим собственный вектор для действительного собственного значения λ= -57,1.

Из третьего уравнения системы видно, что при подстановке в него значения λ₀= –57,1, элемент h3 будет равняться только единице:

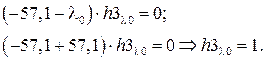
При этом первые два уравнения примут вид:

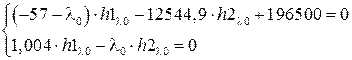
Решим полученную систему уравнений методом обратной матрицы:

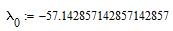
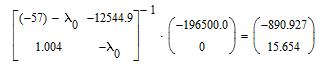
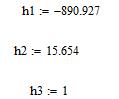
Для комплексно-сопряженных собственных значений достаточно найти только один собственный вектор для одного из собственных значений, например, для .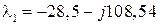

Из системы уравнений для определения собственных векторов видно, что для комплексного корня третий элемент собственного вектора будет равняться нулю:

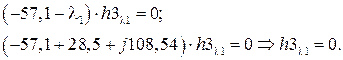
В MathCAD:

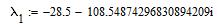
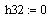
Упростим оставшиеся первые два уравнения:

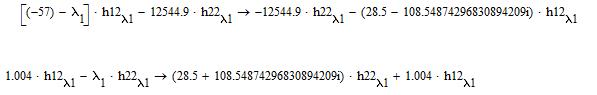
Принимаем:

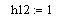
Тогда оставшийся второй элемент собственного вектора будет равен:

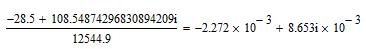
или

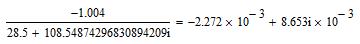
В итоге присваиваем:

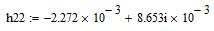
Общее решение однородной системы запишется в виде:

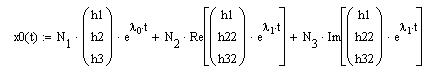
где N₁, N₂, N₃ – константы интегрирования.

Найдем частное решение неоднородной системы:

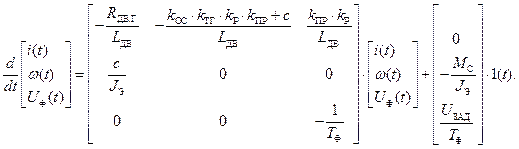
Считаем, что в установившемся режиме при 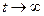производные функций стремятся к нулю. Тогда система неоднородных дифференциальных уравнений представится в виде неоднородной СЛАУ:

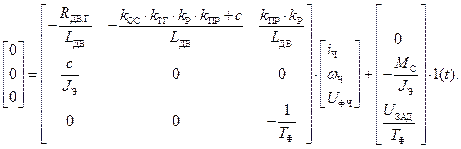
Перенеся свободные члены, получаем:

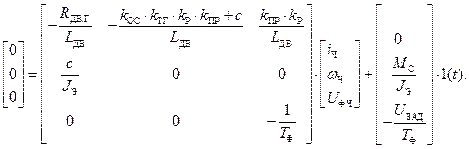
Определим частное решение неоднородной СДУ методом обратной матрицы в программе MathCAD:

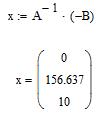
Общее решение неоднородной системы дифференциальных уравнений запишется как сумма общего решения однородной системы и частного решения неоднородной системы:

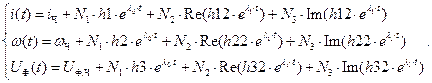
Решим задачу Коши с нулевыми начальными условиями, подставив в общее решение неоднородной СДУ значение времени t=0:

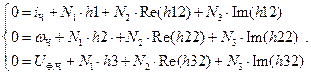
Полученная СЛАУ для нахождения постоянных интегрирования в матричном виде после переноса свободных членов:

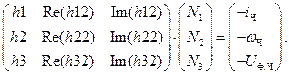
Решим СЛАУ методом обратной матрицы в программной среде MathCAD:

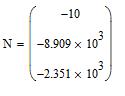
С учетом найденных констант интегрирования запишем аналитические функции, описывающие переходные процессы в ненагруженной ЭМС.

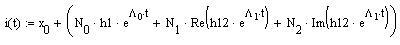
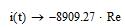
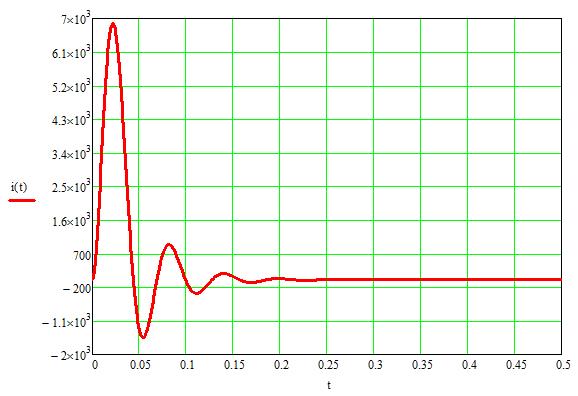
Рисунок 13 – Зависимость i(t), найденная классическим методом

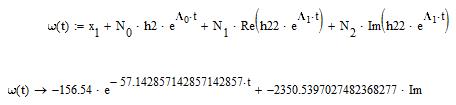
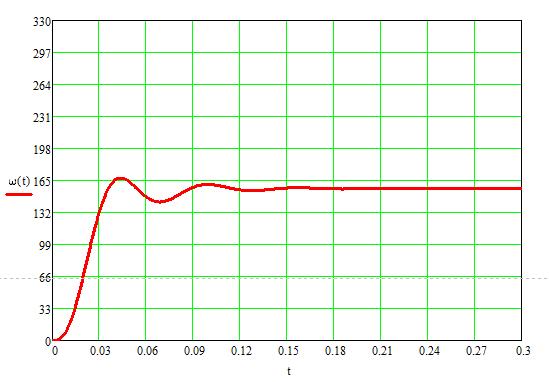
Рисунок 14 – Зависимость 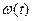, найденная классическим методом

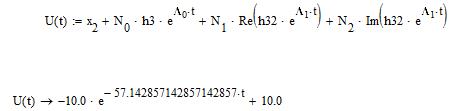
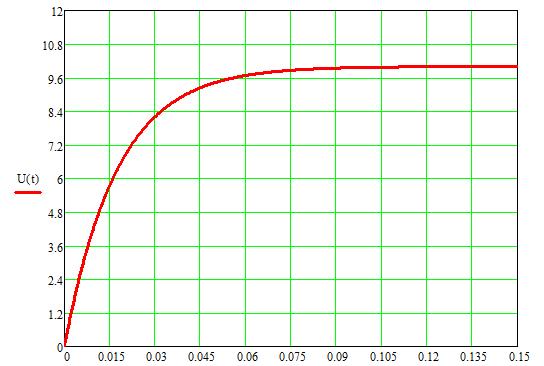
Рисунок 15 – Зависимость U_Ф(t), найденная классическим методом

Полученные характеристики полностью совпали с моделированием в программной среде MATLAB.