Бесконечно малые и бесконечно большие функции
О п р е д е л е н и е 1 Функция  называется беско -нечно малой, в точке
называется беско -нечно малой, в точке  , если
, если 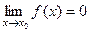
Исходя из этого определения, для того, чтобы для функци  выполнялось равенство
выполнялось равенство  необходимо и достаточно, чтобы функция
необходимо и достаточно, чтобы функция 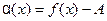 была бесконечно малой при
была бесконечно малой при 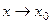 .
.
Отсюда получаем специальное представление для функции, имеющей в точке  предел, равный
предел, равный 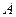 :
:
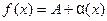 , где
, где 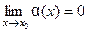
При этом говорят, что в окрестности точки  функция
функция 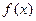 отличается от
отличается от 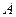 на бесконечно малую функцию.
на бесконечно малую функцию.
Замечание Алгебраическая сумма и произведение конеч -ного числа бесконечно малых функций, а также произведение ограниченной функции на бесконечно малую функцию являют-
ся бесконечно малыми функциями при 
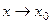 .
.
О п р е д е л е н и е 2. Функция  является беско -нечно большой функцией при
является беско -нечно большой функцией при 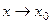 , если для любого
, если для любого 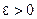 существует
существует 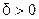 , такое что для всех
, такое что для всех 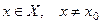 , удо -влетворяющих неравенству
, удо -влетворяющих неравенству 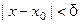 , выполняется нера – венство
, выполняется нера – венство 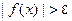 . В этом случае пишут
. В этом случае пишут 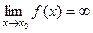 и говорят, что функция
и говорят, что функция 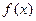 стремится к бесконечности при
стремится к бесконечности при 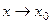 ., или что она имеет бесконечный предел в точке
., или что она имеет бесконечный предел в точке  .
.
Так же как и для последовательностей, для функций имеет место
УТВЕРЖДЕНИЕ. Если при 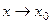
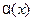 - бесконечно малая функция, то функция
- бесконечно малая функция, то функция 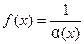 является бесконечно большой и наоборот, если
является бесконечно большой и наоборот, если 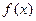 - бесконечно большая функция, то функция
- бесконечно большая функция, то функция 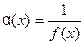 - является бесконечно малой.
- является бесконечно малой.
Например, при 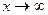 функции
функции 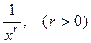 будут бесконечно малыми функциями.
будут бесконечно малыми функциями.
Сравнение бесконечно малых функций.
Пусть при 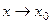 функции
функции 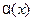 и
и 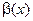 являются бесконечно малыми. Тогда выполняются следующие правила сравнения:
являются бесконечно малыми. Тогда выполняются следующие правила сравнения:
- если
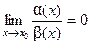 , то
, то 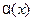 - бесконечно малая более высокого порядка, чем
- бесконечно малая более высокого порядка, чем 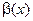 и записываю
и записываю 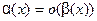 ;
; - если
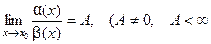 , то говорят, что
, то говорят, что 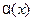 и
и 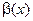 бесконечно малые функции одного порядка;
бесконечно малые функции одного порядка; - если
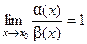 , то говорят, что
, то говорят, что 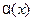 и
и 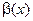 эквивалентные бесконечно малые функции и обозначают
эквивалентные бесконечно малые функции и обозначают 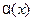 ~
~ 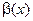 .
.
Например,
1) Функции 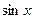 и
и 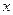 являются эквивалентными бес –
являются эквивалентными бес –
конечно малыми функциями при 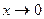 , так как
, так как 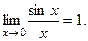 .
.
2) Функции 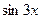 и
и 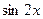 при
при 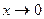 являются беско -нечно малыми функциями одного порядка, так как
являются беско -нечно малыми функциями одного порядка, так как
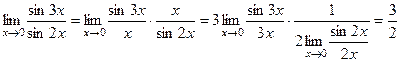 .
.
3) Функция 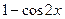 бесконечно малая более высокого порядка, чем
бесконечно малая более высокого порядка, чем 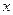 при
при 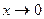 , так как
, так как
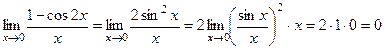 .
.
Важное значение при вычислении пределов имеет так называемая
Таблица эквивалентных бесконечно малых функций:
Если при 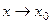 функция
функция 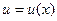 является бесконечно малой, т.е.
является бесконечно малой, т.е. 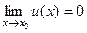 , то можно проверить что следующие функции являются эквивалентными:
, то можно проверить что следующие функции являются эквивалентными:
1. 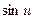 ~
~ 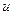 ; 2.
; 2. 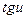 ~
~ 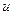 ; 3.
; 3. 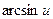 ~
~ 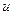 ; 4.
; 4. 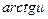 ~
~ 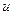 ;
;
5. 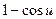 ~
~ 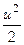 ; 6.
; 6. 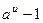 ~
~ 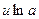 ; 7.
; 7. 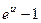 ~
~ 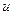 ;
;
8. 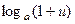 ~
~ 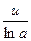 ; 9.
; 9. 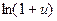 ~
~ 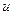 :
:
10. 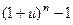 ~
~ 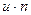 ; 11.
; 11. 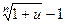 ~
~ 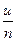 .
.
Чтобы можно было вычислять пределы, используя таблицу эквивалентных бесконечно малых функций важно знать следующий факт.
ТЕОРЕМА. Если при 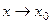 эквивалентны следующие
эквивалентны следующие
бесконечно малые функции : 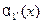 ~
~ 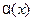 и
и
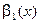 ~
~ 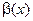 , то выполнено равенство
, то выполнено равенство
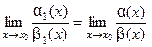 .
.
Например, вычислить предел
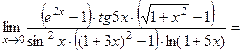
Если мы воспользуемся теперь таблицей, получим
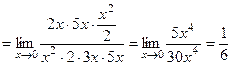 .
.
Таким образом можно вычислять довольно сложные пределы.
Сравнение бесконечно больших функций.
Если при 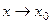 функции
функции 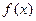 и
и 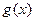 являются бесконечно большими, т.е.
являются бесконечно большими, т.е. 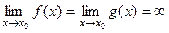 , то также можно привести правила сравнения этих функций:
, то также можно привести правила сравнения этих функций:
1) Если 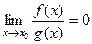 , то говорят, что функция
, то говорят, что функция 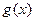 имеет больший порядок роста, чем
имеет больший порядок роста, чем 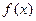 .
.
2) Если 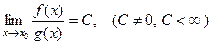 , то говорят, что функции
, то говорят, что функции 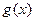 и
и 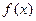 имеют одинаковый порядок роста.
имеют одинаковый порядок роста.
3) Если 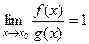 , то говорят, что
, то говорят, что 
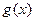 и
и 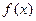 эквивалентные бесконечно большие функции и записывают
эквивалентные бесконечно большие функции и записывают 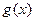 ~
~ 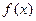 .
.
При вычислении пределов при 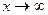 , важно знать, что любой многочлен степени
, важно знать, что любой многочлен степени 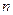 эквивалентен своей старшей степени, т.е.
эквивалентен своей старшей степени, т.е.  ~
~ 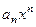 , и при вычислении пределов дробно – рациональных функций, на значение предела влияет только отношение старших степеней. Поэтому, если степень числителя меньше степени знаменателя, то предел равен нулю, если степень числителя больше степени знаменателя, то предел равен
, и при вычислении пределов дробно – рациональных функций, на значение предела влияет только отношение старших степеней. Поэтому, если степень числителя меньше степени знаменателя, то предел равен нулю, если степень числителя больше степени знаменателя, то предел равен 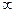 , если степени числителя и знаменателя совпадают, то предел равен отношению коэффициентов перед старшими степенями
, если степени числителя и знаменателя совпадают, то предел равен отношению коэффициентов перед старшими степенями 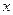 .
.
Например, 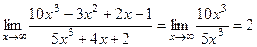 .
.
