Оценка математического ожидания
Оценку математического ожидания получают как среднее арифметическое значение СВ:
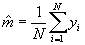 . Сумму лучше всего вычислять (во избежание непроизводительных затрат памяти) путем постепенного накапливания:
. Сумму лучше всего вычислять (во избежание непроизводительных затрат памяти) путем постепенного накапливания: 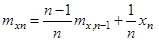 .
.
Оценка дисперсии
Оценку дисперсии можно вычислять по формуле:
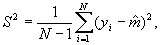
однако это связано с непроизводительным использованием памяти ЭВМ. Поэтому лучше воспользоваться формулой
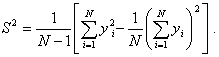
Оценка корреляционного момента
Из тех же соображений, что и для оценки дисперсии, для оценки корреляционного момента двух случайных величин 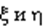 рекомендуется использовать формулу
рекомендуется использовать формулу
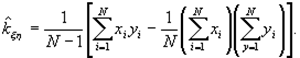
Оценка характеристик случайного процесса
Для вычисления оценки характеристик СП производят статистическую обработку по N реализациям СП. Для этого интервал задания СП разбивают на части с  t=const. Математические ожидания и дисперсии для каждого tk=k
t=const. Математические ожидания и дисперсии для каждого tk=k  t можно вычислить по формулам, приведенным выше. Оценку корреляционной функции - по формуле
t можно вычислить по формулам, приведенным выше. Оценку корреляционной функции - по формуле
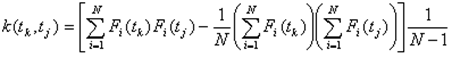
Здесь tk=k  t, tj=j
t, tj=j  t
t
Количество реализаций, обеспечивающих заданную точность
Важной задачей обработки информации является задача определения количества реализаций N, обеспечивающих заданную точность получения оценок. Для определения N при оценке вероятности b пользуются формулой
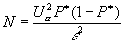 ,
,
а при оценке математического ожидания - 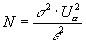 .
.
В формулах 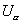 - квантиль, для нормального, центрированного нормального закона распределения, соответствующий значению
- квантиль, для нормального, центрированного нормального закона распределения, соответствующий значению 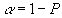 , где P - заданная достоверность;
, где P - заданная достоверность; 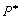 - оцениваемая вероятность;
- оцениваемая вероятность; 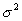 - дисперсия;
- дисперсия; 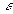 - допустимая погрешность. В этих формулах
- допустимая погрешность. В этих формулах 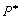 неизвестно, а
неизвестно, а 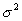 может быть неизвестным. Поэтому производят предварительно 50-100 реализаций, получают по ним оценки
может быть неизвестным. Поэтому производят предварительно 50-100 реализаций, получают по ним оценки 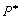 и
и 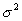 , подставляют их в формулы для вычисления уточненного значения N.
, подставляют их в формулы для вычисления уточненного значения N.
Раздел 3. Основы теории систем массового обслуживания
Введение
Историческая справка
Большинство систем, с которыми человек имеет дело, являются стохастическими. Попытка их математического описания с помощью детерминистических моделей приводит к огрублению истинного положения вещей. При решении задач анализа и проектирования таких систем приходится считаться с положением вещей, когда случайность является определяющей для процессов, протекающих в системах. При этом пренебрежение случайностью, попытка “втиснуть” решение перечисленных задач в детерминистические рамки приводит к искажению, к ошибкам в выводах и практических рекомендациях.
Первые задачи теории систем массового обслуживания (ТСМО) были рассмотрены сотрудником Копенгагенской телефонной компании, датским ученым А.К. Эрлангом (1878- 1929г) в период между 1908 и 1922гг. Эти задачи были вызваны к жизни стремлением упорядочить работу телефонной сети и разработать методы, позволяющие заранее повысить качество обслуживания потребителей в зависимости от числа используемых устройств. Оказалось, что ситуации, возникающие на телефонных станциях, являются типичными не только для телефонной связи. Работа аэродромов, морских и речных портов, магазинов, терминальных классов, электронных вычислительных комплексов, радиолокационных станций и т.д. может быть описана в рамках ТСМО.
