Решение задачи математическими методами
Постановка задачи
В универсаме к узлу расчета поступает поток покупателей с интенсивностью λ = 81 человек в час. Средняя продолжительность обслуживания контролером-кассиром одного покупателя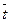 
об. = 2 минуты. Рабочее время 8 часов (1 час обеденный перерыв). Средняя з/п одного контролера-кассира составляет 5000руб. в месяц. Кассовый аппарат стоит 3000руб. (срок службы 5 лет). Стоимость канцтоваров (бумага, кассовая лента, ручки и т.д.) на одного кассира составляет 150 руб. в месяц.
Арендная плата в месяц составляет 10000 руб. Коммунальные услуги составляют 2000 руб. Налоги составляют 5670 руб.
Средний размер покупки - 100руб.
Определить:
Минимальное количество контролеров-кассиров nmin, при котором очередь не будет расти до бесконечности, соответствующие характеристики обслуживания при 
n=nmin и прибыль фирмы при этих условиях.
Решение задачи
Задача представляет собой яркий пример СМО с ожиданием.
Необходимо найти:
Минимальное количество контролеров-кассиров nmin, при котором очередь не будет расти до бесконечности, соответствующие характеристики обслуживания при n=nmin и прибыль фирмы при этих условиях.
Находим среднее число занятых каналов по формуле 1.31.
По условию l=81 (1/ч) =1.35 (1/мин).
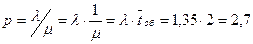
Очередь не будет расти до бесконечности при условии, что среднее число занятых каналов будет меньше, чем реальное количество кассиров. На числовой оси наименьшее натуральное целое число, большее, чем 2,7, есть число 3. Значит минимальное количество кассиров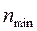 
=3.
Рассчитаем основные характеристики этой СМО с количеством кассиров 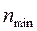=3. Вероятность того, что канал свободен. По формуле (1.27) получаем:
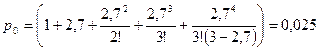
Таким образом, можно заключить, что 2,5% времени касса свободна.
Вероятность того, что заявка окажется в очереди, рассчитаем по формуле 1.30:
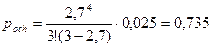
Среднее число заявок в очереди. Воспользовавшись формулой 1.31, получаем:
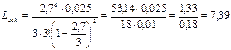
Среднее время ожидания в очереди
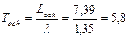
Среднее число заявок в системе
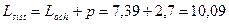
Рассчитаем прибыль фирмы при этих условиях.
Прибыль = выручка - себестоимость. На себестоимость продукции отнесем заработную плату 3х кассиров, амортизационные отчисления от использования основных средств (кассовые аппараты), материальные затраты на канцелярию, арендную плату, затраты на коммунальные услуги, а также начисленные предприятию налоги. При расчете заработной платы будем считать, что фирма работает без выходных, а отчетный период равен 30 дням.
З/П.3х кассиров = 3 кассира*5 т. р. =15 т. р.
Начислена амортизация основных средств:
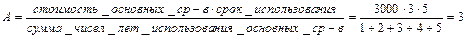т. р.
Материальные затраты на канцелярию 150*3=0,45 т. р.
Арендная плата = 10 т. р.
Затраты на коммунальные услуги = 2 т. р.
Начисленные предприятию налоги = 5,670 т. р.
Значит себестоимость по осуществлению предпринимательской деятельности предприятия = 15+3+0,45+10+2+5,670=36,12 т. р.
Рассчитаем выручку с учетом данных задачи об интенсивности обслуживания. Если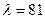 
человек в час, то можем посчитать, сколько людей обслуживается одним кассиром за месяц: 
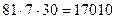человек.
Теперь можем определить размер выручки: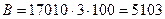 
т. р.
Прибыль = 5103-36,12 =5066,88 т. р.
Заключение
Математическое программирование и стохастическое моделирование имеют широкий диапазон применения
Сравнивая решение практической задачи в данной курсовой математическими методами, можно говорить о том, что, несомненно, компьютерное моделирование заметно облегчает процесс принятия решения по конкретному вопросу.
Решение математическими методами более полно охватывает все характеристики интересующего вопроса, и отражают картину функционирования системы с разных точек зрения.
Решение математическими методами приводит к выводу о том, что оптимальное число кассиров в СМО "Универсам" должно быть равно шести, т.к. именно количество каналов обслуживания отражается на относительной величине затрат, связанной с издержками на содержание каналов обслуживания и с пребыванием
очереди покупателей, задаваемая, по условию задачи, как
Cотн=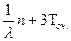 
Литература
1. Анализ систем массового обслуживания с использованием программного комплекса "Теория Массового Обслуживания". Методические указания. Издательство ИГЭА. 2001.
2. Александрова Е.А. Теория массового обслуживания в задачах оптимизации. Статья. Вольное экономическое общество России. 2009.
3. Т.Я. Лазарева, И.В. Диденко. Системы массового обслуживания: методические разработки. Тамбов: Тамбовский государственный технический университет. 2001.