Краткие теоретические сведения по теме работы

Лабораторная работа № 1

По дисциплине: «Теория и практика технического эксперимента»

На тему: «Базовые понятия теории вероятности »

Специальность: электроснабжение промышленных предприятий

Выполнила: Оралкызы Г. Группа МЭППп-15

№ зачетной книжки: 154М009

Принял: Айткулов Н.С.

_________________ «____ » ____________ 2015 г.

Алматы 2015

Цель работы:

в результате выполнения работы учащиеся должны знать и уметь объяснять основные понятия и определения теории вероятности в пределах лекционного курса, а также прибрести практические навыки: а) по вычислению основных параметров исследуемых данных: математического ожидания, дисперсии и среднего квадратичного отклонения и б) по построению кривых нормального распределения.

При выполнении работы учащиеся должны уметь применять необходимые для вычислений и построения графиков инструменты Excel.

Краткие теоретические сведения по теме работы

В теории вероятностей изучаются закономерности для случайных событий. Случайные события – это такие события, результат которых заранее предсказать невозможно. В теории вероятностей каждое такое событие принято характеризовать численной мерой возможности события. Эта численная мера называется вероятностью. Вероятность — это число в диапазоне от 0 до 1.

Случайные величины бывают дискретными инепрерывными. Возможными реализациями дискретной случайной величины являются отдельные числа, в то время как непрерывная случайная величина может принимать непрерывный набор значений.

Важное место в наборе числовых характеристик случайных величин занимает математическое ожидание, которое для непрерывной случайной величины, определяется по формуле:

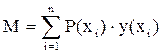, (1)

а для дискретной величины по формуле:

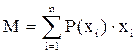(2)

Математическое ожидание характеризует центр, вокруг которого группируются случайные величины.

Кроме математического ожидания важной характеристикой является дисперсия.

Дисперсией случайной величины называют ее числовую характеристику, которая определяется для непрерывной случайной величины по формуле:

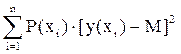, (3)

а для дискретной случайной величины по формуле:

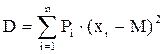. (4)

Дисперсия характеризует степень разброса или отклонений случайных величин от своего центра – математического ожидания.

Большинство экспериментальных исследований в технике и в различных областях естественных наук, связаны с измерениями, результаты которых могут быть описаны с помощью кривой нормального распределения, которое задает­ся формулой Гаусса:

,

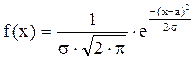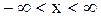
Здесь а - математическое ожидание

- среднее квадратичное отклонение. (5)

График нормальной кривой представлен на рисунке 1

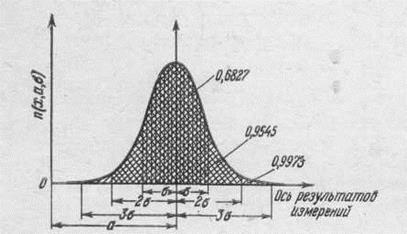
Рисунок 1 - Нормальная кривая распределения.

Случайные величины, изменяющиеся по нормальному закону, группируются вокруг некоторого центра, равному математическому ожиданию. А площадь кривой, построенной на каком - либо диапазоне изменения случайных величин, будет равна вероятности появления этих величин.

Например, для случайных величин находящихся в интервале 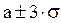вероятность их появления равна 0,997. Можно утверждать, что лишь ничтожная часть случайных величин будет находиться вне указанного предела. Последняя закономерность называется, правилом трех сигм или правилом трех стандартов.

Практическая работа включает в себя 2 задания.

Задание 1

Тема: Определение основных характеристик для непрерывных и дискретных случайных величин.

Дано:

ряд значений случайных величин 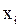, вероятности их появления 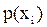, а также функция 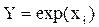для непрерывных случайных величин. Данные приведены в файле «Исходные данные к заданию 1.1».

Требуется:

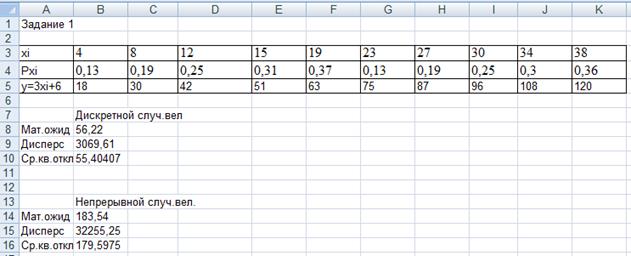
рассчитать математическое ожидание, дисперсию и среднее квадратичное отклонение по формулам теории вероятности.

1.2 Методические указания по выполнению задания 1.

Для нахождения математического ожидания дискретных случайных величин следует применить формулу (2). После чего по формуле (4) найти дисперсию, а затем по формуле (5) среднее квадратичное отклонение.

Для нахождения математического ожидания для непрерывных случайных величин следует применить формулу (1). После чего по формуле (3) найти дисперсию и по формуле (5) среднее квадратичное отклонение.

Данные к заданию 1 учащиеся получают с помощью программы «Исходные данные к заданию 1», в которой вариант задания и исходные данные задаются с помощью генератора случайных чисел. Полученные данные заверяются подписью преподавателя, и листок с заверенными данными вкладывается (вклеивается) в отчет по работе.

Задание 2

Тема: Построение кривых нормального распределения

Дано:

ряд значений математического ожидания М и среднего квадратичного отклонения s, приведенные в файле «Исходные данные к заданию 1.2.

Требуется:

построить по этим данным ряд кривых нормального распределения для двух случаев:

В первом случае меняются математические ожидания (М₁ и М₂), а среднеквадратичное отклонение (s) остается неизменным.

Во втором случае меняются среднеквадратичные отклонения (s₁, s₂, и s₃), а математическое ожидание (М) остается неизменным.

написать в отчете по работе выводы о характере влияния значения математического ожидания и среднего квадратичного отклонения на форму кривой.