Оценивание корреляционных функций
Прежде всего, рассмотрим оценку корреляционной функции для стационарного случайного процесса [Y(t)]. Эта оценка производится с помощью формулы
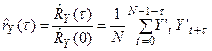 , (81)
, (81)
где
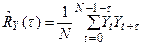 -оценка ковариационной функции, а
-оценка ковариационной функции, а 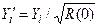 .
.
Оценка, получаемая с помощью формулы (81), является нелинейной функцией величин 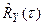 и
и 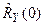 . При исследовании свойств этих оценок обычно прибегают к их линеаризации. Линеаризация сводится к разложению функции
. При исследовании свойств этих оценок обычно прибегают к их линеаризации. Линеаризация сводится к разложению функции
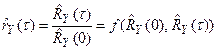
в ряд Тейлора в окрестности точки 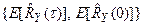 , сохраняя только линейные члены. При этом предполагается, что отклонения случайных величин
, сохраняя только линейные члены. При этом предполагается, что отклонения случайных величин 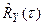 ,
, 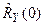 от их математических ожиданий невелики и, с достаточно большой вероятностью нелинейными членами можно пренебречь.
от их математических ожиданий невелики и, с достаточно большой вероятностью нелинейными членами можно пренебречь.
Разложение имеет вид
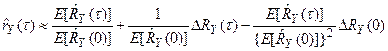 , (82)
, (82)
где
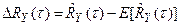 ,
, 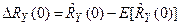 .
.
В выражении (82) сохранены только линейные члены разложения. Согласно полученным ранее оценкам и свойствам ковариационных функций можно записать,
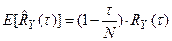 . (83)
. (83)
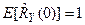 . (84)
. (84)
С учетом (83) и (84) получим из (82) следующее выражение для оценки корреляционной функции и математического ожидания корреляционной функции
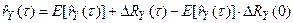 (85)
(85)
и
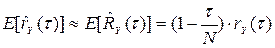 . (86)
. (86)
Из (86) следует, что оценка корреляционной функции асимптотически не смещена.
Дисперсия оценки корреляционной функции может быть определена следующим образом
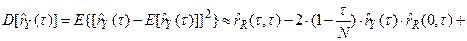
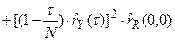 . (87)
. (87)
Из формулы (87) следует состоятельность оценки (81). Формула (87) показывает также, что, чем выше коррелированность точек исходного ряда, тем большая дисперсия соответствует получаемым оценкам.
При оценивании дисперсии пространственной корреляционной функции используют простое соотношение, которое получается в случае, если реализации поля считаются независимыми. Это соотношение имеет вид
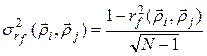 . (88)
. (88)
Эта формула позволяет сделать вывод о том, что для пар точек, для которых имеет место тесная связь, требуется меньший объем данных, чем для станций со слабой связью случайных величин.
Из формулы (88) можно получить объем выборки, необходимый для оценки коэффициента корреляции с заданной точностью. Такие оценки приведены в табл. 2.
Зная дисперсию оценки корреляционной функции, можно определить доверительный интервал для коэффициента корреляции при заданном уровне значимости q. Доверительный интервал определяется следующим выражением
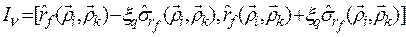 , (89)
, (89)
где  — доверительная вероятность, q — уровень значимости; ξq — квантиль распределения Стъюдента. Наиболее часто доверительную вероятность принимают равной 95%, 99%. В этом случае ξq соответственно равна 1,96 и 2,58.
— доверительная вероятность, q — уровень значимости; ξq — квантиль распределения Стъюдента. Наиболее часто доверительную вероятность принимают равной 95%, 99%. В этом случае ξq соответственно равна 1,96 и 2,58.
Таблица 2
Количество наблюдений, необходимых для получения корреляционной функции с заданной точностью
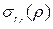 | 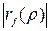 | ||||||||
| 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0,4 | 0,3 | 0,2 | 0,1 | |
| 0,05 | |||||||||
| 0,02 | |||||||||
| 0,01 |
Формула (89) получена при условии, что распределение оценки близко к нормальному при данном объеме выборки N. На самом же деле распределение оценки (81) стремится к нормальному очень медленно при увеличении величины N. Если выборка является не очень большой, то, как правило, для оценки точности коэффициента корреляции пользуются случайной величиной
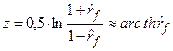 . (90)
. (90)
Эта величина,определяемая преобразованием коэффициента корреляции, называемым преобразованием Р. Фишера, значительно быстрее стремится к нормальному закону с увеличением N, чем оценка 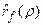 . Математическое ожидание этой величины и ее дисперсия определяются следующим равенством
. Математическое ожидание этой величины и ее дисперсия определяются следующим равенством
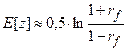 , (91)
, (91)
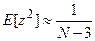 . (92)
. (92)
Оценив значение z по формуле (90), строят для этой величины доверительный интервал, задаваясь той или иной доверительной вероятностью
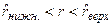 , (93)
, (93)
где

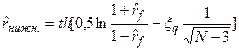 , (94)
, (94)
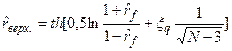 . (95)
. (95)
Значения верхней и нижней границы доверительного интервала при 5%-ном уровне значимости q могут быть найдены по справочникам. В качестве zкр принимается величина
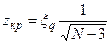 , (96)
, (96)
где ξq = 1,96.
Если при расчете коэффициента корреляции оказывается, что соответствующее ему значение z > zкр, то для заданного уровня значимости (в данном случае 5%) вычисленное значение коэффициента корреляции значимо отличается от нуля. Расчеты показывают, что значениями, отличающимися от нуля, могут считаться коэффициенты корреляции 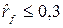 при объемах выборок 250, 200 и 150.
при объемах выборок 250, 200 и 150.
