Вычисление двойного интеграла в полярной системе координат

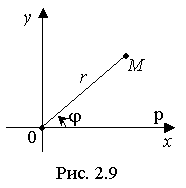
Пусть на плоскости Оху одновременно введена и полярная система координат Orφ (рис. 2.9):

Оp - полярная ось, которая совпадает с осью Ох;
φ - полярный угол;
r - полярный радиус точки М.

Тогда, как известно:

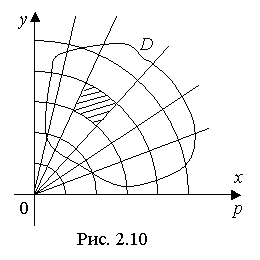
Для полярной системы координатная сетка представляет собой пересечение окружностей увеличивающихся радиусов r с лучами, выходящими из точки О под возрастающими углами φ к полярной оси (рис. 2.10).

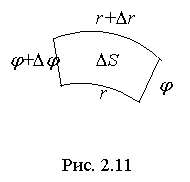
Рассмотрим элементарный участок полярной сетки (рис. 2.11).

Тогда его площадь ΔS можно найти как разность площадей S₁ и S₂ полярных секторов радиусов r+Δr и r с раствором угла Δφ:

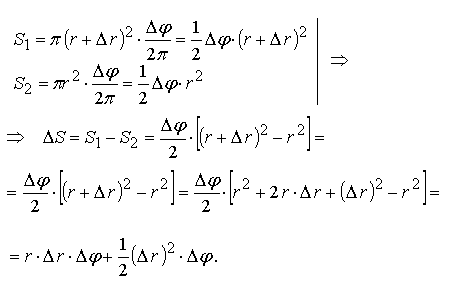
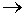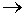При Δr 0, Δφ 0 получаем ΔS≈ r·Δr·Δφ.

Таким образом, при замене переменных по формуле (2.12) дифференциал площади в полярной системе координат преобразуется так:

(Напомним, что в декартовой системе координат Оху прямоугольная сетка дает dS=dx·dy.)

Замечание.

Формулу (2.13) можно получить и по-другому, используя Якобиан J - "коэффициент искажения" площади при переходе к другой системе координат. А именно

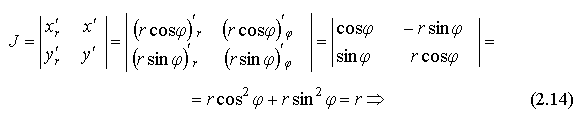
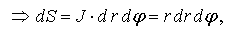что совпадает с (2.13).

Теорема

Если область D - является правильной в полярной системе координат Оrφ, то двойной интеграл в этих координатах вычисляется так: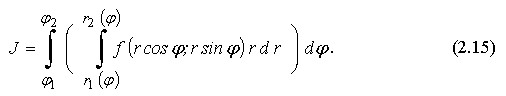

Тройной интеграл.

Чтобы ввести понятие тройного интеграла, предварительно рассмотрим задачу о нахождении массы тела переменной плотности.

Пусть в системе координат Оxyz (рис. 2.18) задано некоторое ограниченное тело U с переменной плотностью γ=f(x;y;z)>0, (x;y;z) 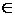U.

Требуется приближенно вычислить массу этого тела.

Для этого разрежем это тело на n "достаточно мелких частей" ΔU_i,i=1,2,...,n.

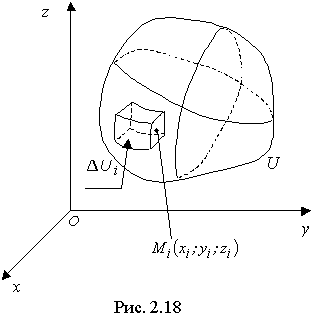
Внутри этого "кусочка" можно принять, что γ ≡ const=f(M_i), где M_i(x;y;z) - некая "средняя" точка в ΔU_i.

Обозначим объём "кусочка" ΔU_i через ΔV_i, тогда масса "кусочка" ΔM_i: ΔM_i≈f(M_i)·ΔV_i. А для всего тела: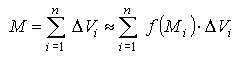

√ получена интегральная сумма.

Затем переходим к пределу при n 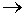∞ и ΔV_i 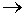0, i=1,2,...,n и получаем: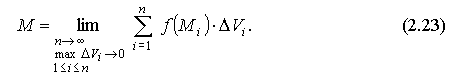

Если предел (2.23) интегральной суммы существует, то он называется тройным интегралом от функции f(x;y;z) по объему U и обозначается: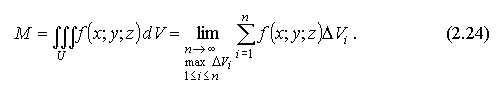

После этого можно сформулировать более точное и общее определение тройного интеграла.

Определение

Пусть f(x;y;z), (x;y;z) 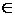U - произвольная функция трех переменных, U - ограниченная трехмерная область.

Разобьем U произвольным образом на части ΔU₁, ΔU₂,...,ΔU_n. В каждой из них возьмем произвольную точку M_i(x_i;y_i;z_i) 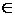U_i и составим интегральную сумму:

Если существует предел интегральной суммы: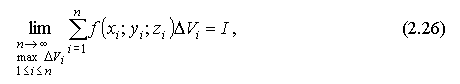

не зависящий от способа разбиения U на n частей ΔU₁, ΔU₂,...,ΔU_n, а также от произвола в выборе точек M_i 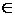U_i, то этот предел I обозначается через 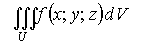и называется тройным интегралом от функции f(x;y;z) по объёму U. При этом функция f(x;y;z) называется интегрируемой по U.

Теорема

Если f(x;y;z), (x;y;z) 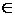U непрерывна, то она интегрируема по U.

Определение

Тройные интегралы от непрерывных функций называются собственными тройными интегралами (или просто тройными интегралами), а тройные интегралы от разрывных функций - несобственными тройными интегралами.

В дальнейшем считаем, что все появляющиеся в тексте функции (если это не оговорено особо) интегрируемы по объёму.

*********************