Построение системы цифровой коррекции
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
«Московский государственный университет приборостроения и информатики»
Факультет (филиал) ___________ специальность (направление) 200100
Кафедра ПР-1 «Точные приборы и измерительные системы»
Дисциплина «Разработка устройств на базе цифровых процессоров обработки сигналов»
Курсовая работа
На тему:
«Разработка системы цифровой коррекции динамических характеристик первичного преобразователя измерительной системы»
Студент ______________ ______________ Тихонов Д. Н.
подпись дата фамилия, инициалы
Группа СППР1-12-01з шифр 120122з
Проект(работа) защищен(а) на оценку_______________________________
Руководитель проекта ____________ __________ Кононов М. А.
подпись дата фамилия, инициалы
Задание на курсовую работу:
В качестве исходных данных используются оцифрованные значения переходного процесса исследуемого первичного преобразователя (и градуированной характеристики при необходимости коррекции нелинейных искажений).
Исходные данные – блок wn.
Содержание
Введение. 4
Построение системы цифровой коррекции. 6
Методика проведения фильтрации сигналов. 9
Заключение. 14
Список использованных источников. 15
Введение
Любой непрерывный (аналоговый) сигнал может быть подвергнут дискретизации по времени и квантованию по уровню (оцифровке), то есть представлен в цифровой форме. Если частота дискретизации сигнала не меньше, чем удвоенная наивысшая частота в спектре сигнала, то полученный дискретный сигнал эквивалентен сигналу. При помощи математических алгоритмов преобразуется в некоторый другой сигнал имеющий требуемые свойства. Процесс преобразования сигналов называется фильтрацией, а устройство, выполняющее фильтрацию, называется фильтр. Поскольку отсчеты сигналов поступают с постоянной скоростью, фильтр должен успевать обрабатывать текущий отсчет до поступления следующего (чаще – до поступления следующих отсчетов), то есть обрабатывать сигнал в реальном времени. Для обработки сигналов (фильтрации) в реальном времени применяют специальные вычислительные устройства – цифровые сигнальные процессоры.
Все это полностью применимо не только к непрерывным сигналам, но и к прерывистым, а так же к сигналам, записанным на запоминающие устройства. В последнем случае скорость обработки не принципиальна, так как при медленной обработке данные не будут потеряны.
Обработка сигналов во временной области широко используется в современной электронной осциллографии и в цифровых осциллографах. А для представления сигналов в частной области используются цифровые анализаторы спектра. Для изучения математических аспектов обработки сигналов используются пакеты расширения (чаще всего под именем Signal Processing) систем компьютерной математики MATLAB, Mathcad, Maple и др.
В последние годы при обработке сигналов и изображений широко используется новый математический базис представления сигналов с помощью «коротких волночек» - вейвлетов. С его помощью могут обрабатываться нестационарные сигналы, сигналы с разрывами и иными особенностями и сигналы в виде пачек.
Построение системы цифровой коррекции
Система цифровой коррекции моделируется в компьютерном приложении MATLAB Simulink.
На вход системы подается идеальный единичный скачок (cтупенька).
В Simulink это осуществляется добавлением на рабочее поле программы элемента Step с параметрами Step time = 1, Initial value = 0, Sample time = 0.1.
Ступенька подается на блок wn, указанный в задании на курсовую работу. Блок содержит помеху, которую необходимо отфильтровать для получения на выходе системы ступеньки.
Выход блока wn соединяется с моделью осциллографа Scope через звено дискретизации (элемент Zero-Order Hold с параметрами Sample time = 0.565).
Полученная первоначальная модель формирования сигналов изображена на рисунке 1. Сигнал на выходе блока изображен на рисунке 2.
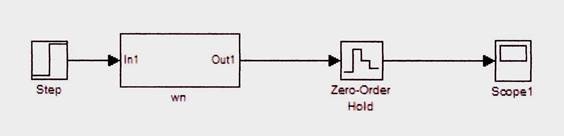
Рис 1. Модель формирования сигналов
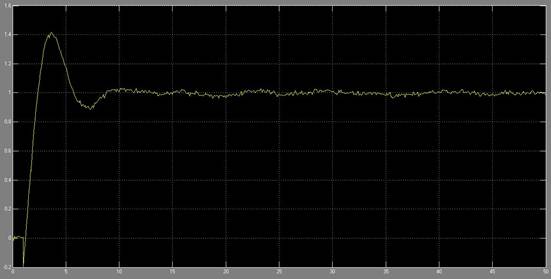
Рис 2. Сигнал на выходе блока wn
Как видно из рисунка, сигнал на выходе блока wn сильно отличается от идеальной ступеньки, поданной на вход. Поэтому для фильтрации сигнала необходимо поместить на рабочее поле программы блок дифференциатора Discrete Derivative с параметрами, заданными в Simulink по умолчанию, и блок цифрового фильтра Discrete Filter с параметрами Denominator = [1], Sample time = 0.565. На выходе каждого из блоков необходимо поставить модель осцилографа Scope 2 и Scope 3 соответственно для контроля сигнала после каждого блока.
Полученная модель системы цифровой коррекции приведена на рисунке 3.
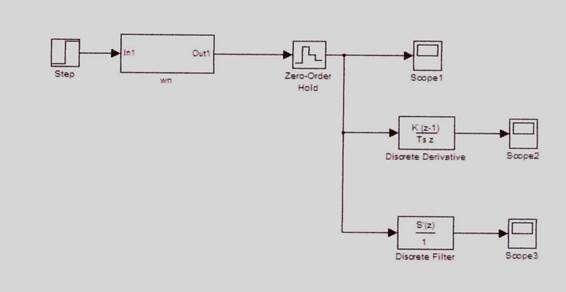
Рис 3. Модель системы цифровой коррекции сигналов
