Разностью двух множеств называется совокупность элементов первого множества, не принадлежащих второму множеству
| А\В |
| В |
А\В={ 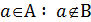 }. }. |
Это равенство определяет разность двух множеств как совокупность элементов первого множества, не принадлежащих второму множеству. Для предыдущего примера
{1, 3, 2}\{3, -5, 6, 1}={2}.
Очевидно также, что
А\A=Æ.
Поскольку пересечение множеств условно говоря сокращает (“уменьшает”) каждое из них, а объединение расширяет (“увеличивает”), то для любых множеств А и В справедливо включение
| А∩ВÌАÌА∪В. |
Универсальное множество U содержит все множества, связанные с рассматриваемой задачей. Дополнение множества А ÍU обозначается 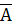 и представляет собой совокупность элементов U, не принадлежащих А;
и представляет собой совокупность элементов U, не принадлежащих А;
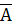 ={ ={ 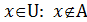 }. }. |
Очевидно, что 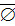 =U,
=U, 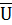 =Æ.
=Æ.
Пример. Все обучающиеся лица - U, а студенты вузов - А. Тогда 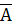 - все учащиеся не студенты.
- все учащиеся не студенты.
Операции над множествами обладают следующими свойствами.
1. Идемпотентность:
| А∪А=А, А∩А=А. |
2. Коммутативность (однозначность результата вне зависимости от порядка объектов операции):
| А∪В= В∪А, А∩В=В∩А. |
3. Ассоциативность (однозначность результата вне зависимости от порядка исполнения операций):
| А∪(В∪С)=(А∪В)∪С, А∩(В∩С)=(А∩В)∩С . |
Здесь скобки подобно арифметике определяют приоритет операций. При отсутствии скобок сначала выполняются операции пересечения, а затем объединения.
4. Дистрибутивность:
| А∪(В∩С)=(А∪В)∩( А∪С), А∩( В∪С)=(А∩В)∪(А∩С). |
5. Очевидные результаты операций, следующие из их определений и
особых типов множеств (Æ, U, 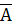 ):
):
А∪Æ=А, A∩Æ=Æ, А\А=Æ, A∩U=A, A∪U=U, А∪ 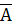 =U, =U, 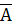 =U\А. =U\А. |
Нетрудно убедиться в справедливости перечисленных ниже тождеств.
1. Если А∪В=А при всех А, то В=Æ. 2. Если А∩В=А при всех А, то В=U. 3. Если А∪В=U и А∩В=Æ, то В= 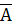 . 4. Двойное дополнение множества дает его само, т.е. . 4. Двойное дополнение множества дает его само, т.е. 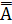 =А. 5. Законы двойственности де Моргана: =А. 5. Законы двойственности де Моргана: 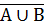 = = 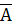 ∩ ∩ 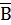 , , 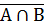 = = 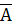 ∪ ∪ 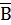 . . |
ПРАКТИКУМ
1. Формализовать описание множества действительных чисел,
делящихся нацело на 2.5
G={𝑥ÎR: 𝑥/2.5ÎN }.
2. Дать описание круга радиуса 𝑟 c центром в начале координат как
геометрического места точек
{(𝑥, 𝑦)Î 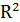 :
: 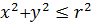 }.
}.
3. Описать положительную полуось абсцисс на плоскости
{(𝑥, 𝑦)Î 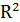 : 𝑥>0, 𝑦=0}.
: 𝑥>0, 𝑦=0}.
4. Если
А={𝑛ÎN: 𝑛=2𝑘, 𝑘ÎN} - множество положительных четных целых
чисел и
В={𝑛ÎN: 𝑛=3𝑘, 𝑘ÎN} - множество положительных целых чисел,
кратных 3,
то
А∪В= {𝑛ÎN: 𝑛=2𝑘 или 𝑛=3𝑘, 𝑘ÎN} - множество положительных
целых чисел, кратных 2 или 3,
А∩В= {𝑛ÎN: 𝑛=2𝑘 и 𝑛=3𝑘, 𝑘ÎN}={𝑛ÎN: 𝑛=6𝑘, 𝑘ÎN} - множество положительных целых чисел кратных сразу 2 и 3, а, следовательно,
и их произведению, т.е. 6.
5. Пусть
P={“⊿”} - множество прямоугольных треугольников,
F={”Δ”} - множество равнобедренных треугольников.
Тогда
P∪F={“⊿” или ”Δ”} - множество прямоугольных или
равнобедренных треугольников или и
тех и других,
P∩F={“⊿” и ”Δ”} - множество равнобедренных и в то же
время прямоугольных треугольников.
6. Доказать, что
А∪(А∩В)=А, А∩( А∪В)=А.
Поскольку, следуя правилам, сначала надлежит выполнить
операции, описанные в скобках, то в первом соотношении
множество А объединяется с его же частью, что своим
итогом имеет, конечно же А. Левая часть второго равенства
в результате пересечения множества А с множеством “бóльшим”
чем А естественно дает само А.
7. Лекции по математике слушают 20, а по информатике - 40
студентов. Сколько учащихся слушают лекции по математике
или информатике, если лекции по обоим предметам проходят:
- в одни часы;
- в разное время и 15 студентов слушают оба предмета.
| А×В |
8. Для множеств А={1, 5, 3, 2} и В={2, 3, 1} какое из перечисленных
ниже утверждений будет правильным:
1) “Множества А и В равны” 2) “А является подмножеством В”
3) “В есть подмножество А” 4) “Множества А и В не равны”
5) “Множества А и В не имеют общих элементов”
До равенства множеству В не хватает элемента {5}, т.е.
А=В∪{5} и потому первый вариант ответа неверен. Поскольку все
элементы множества В в то же время являются элементами А
(А “больше” В), очевидно, правильным будет ответ под номером 3
(ВÌА) - А включает (содержит) В или В принадлежит А, а ответ
под номером 2 - ошибочен. Вариант 4 является еще одним пра-
вильным ответом. Вариант 5 неверен.
9. Расположить результаты приведенных ниже операций над произ-
вольными множествами А, В и С так, чтобы каждый из них был
подмножеством последующего:
1) А∪В∪С 2) А∩В∩С 3) В∪С 4) А∩(В∪С).
В качестве ответа надо указать правильную последовательность
номеров операций. Учитывая, что пересечение множеств “меньше”,
а объединение “больше” каждого из них, то начинать цепочку
вложений будет номер 2 (самое “маленькое”), а замыкать ее - 1
(самое “большое”). Номер 4 “меньше” номера 3, будучи пересече-
нием с номером 3. Следовательно, верным будет ответ 2- 4-3-1.
10. Для множеств М={a, b, c, d} и N={b, c, d, e, f, g} установить соответ-
ствие результатов операций предлагаемым вариантам ответов.
Операция: Варианты ответов:
1) M∪N A) {a}
2) M∩N B) {b, c, d}
3) M\N C) {a, b, c, d, e, f, g}
4) N\M D) {e, f, g}
Устанавливая соответствие операций ответам по номерам надо
указать правильную последовательность ответов из числа предла-
гаемых вариантов, следуя правилам приведенных операций. Тако-
вой будет последовательность C-В-A-D.
11.Установить последовательность вложения для множеств N, Z, Q, R.
По определению этих множеств верным будет ответ NÌZÌQÌR.
12.Какое из перечисленных ниже утверждений будет верным?
1) 15ÎN 2) 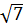 ÎZ 3) 4,1ÎN 4)
ÎZ 3) 4,1ÎN 4) 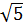 ÎQ 5)
ÎQ 5) 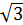 ÎR 6)
ÎR 6) 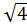 ÎZ 7)
ÎZ 7) 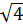 ÎN
ÎN
По определению числовых множеств верными будут ответы под
номерами 1, 5 и 6. Ответы 2, 3, 4 и 7 неверны. Последние два
варианта ответов дают ±2 и в соответствии с предыдущей зада-
чей множество {-2, 2}ÌZÌQÌR, т.е. ответ 6 верен, а 7 - ошибочен,
т.к. -2ÏN.
13.Декартовым произведением множеств A={1, -3, 3} и B={-1, 2}
будет:
1) {(-1, 1), (-1, -3), (-1, 3), (2, 1), (2, -3), (2, 3)} 2) {Æ}
3) {(1, -1), (1, 2), (-3, -1), (-3, 2), (3, -1), (3, 2)} 4) {1, -3, 3, -1, 2}
Только ответ 3 является верным, поскольку именно он образован
парами, в которых на первом месте стоит элемент первого мно-
жества, а на втором месте - элемент второго множества. Первый
вариант является результатом В´А, второй - А∩В, четвертый -
А∪В.
