Исследовательская часть
Исследуем, как будут меняться функции v, y, x,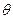 
в зависимости от подстановки в уравнения движения неуправляемого летательного аппарата в проекциях на касательную и нормаль к траектории значений коэффициента свободного падения с разной точностью задания (см. табл. 6, 7).
Таблица 6: Расчёт активного участка
Скорость vа,  | Угол θа | Высота yа, м | Дальность xа, м | Время tа, с | Коэф. своб. падения g  | |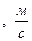
| Метод Рунге-Кутта | 432.42 | 0.574 | 552.47 | 789.37 | 9.81 | |
| 432.10 | 0.569 | 549.17 | 790.83 | |||
| Метод Эйлера | 0.575 | 565.39 | 807.67 | 9.81 | ||
| 447.09 | 0.570 | 561.19 | 808.16 |
Таблица 7: Расчёт пассивного участка
| Скорость vп, | Угол θп | Высота yп, м | Дальность xп, м | Время tп, с | Коэф. своб. падения g | |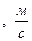
| Метод Рунге-Кутта | 237.377 | -0.906 | 10426.327 | 46,488 | 9.81 | |
| 238.600 | -0.900 | 10288.818 | 45.558 | |||
| Метод Эйлера | 240.461 | -0.914 | 10884.580 | 47.618 | 9.81 | |
| 241.703 | -0.908 | 10744.871 | 46.668 |
Из таблиц 6 и 7 видно, что изменение величины коэффициента свободного падения g в пределах (9.81 - 10)м/с существенным образом не оказывает влияние на функции v, y, 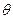. Изменение коэффициента свободного падения g более существенно влияет только на дальность x.
Исследуем точность метода Рунге-Кутта и метода Эйлера на примере дальности неуправляемого ЛА xп. Точность в этих методах определяется заданием шага интегрирования 
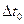. Будем 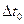последовательно делить на 2, если точность велика, и 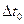последовательно умножать на 2, в случае, если точность удовлетворяет (см.табл.8).
Таблица 8
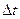 | Дальность xп, м | |
| Метод Рунге-Кутта | 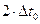 =0.02 | 10452.093 |
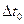| =0.01 | 10426.327 | |
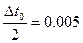 | 10426.866 | |
| Метод Эйлера | 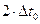=0.02 | 10573.747 |
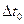| =0.01 | 10884.580 | |
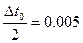| | 10885.449 |
8 видно, что шаг 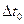=0.01 выбран верно, т.к. при 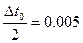изменение значения дальности полёта неуправляемого ЛА незначительно, а при 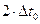=0.10 изменение дальности полёта уже существенно.
Исследуем поведение функции v, y, x, 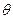в зависимости от времени t при постоянном коэффициенте лобового сопротивления Cx. В качестве значений Cx возьмём: 0.157; 0.181; 0.567.
V(t):
Cx=0.157
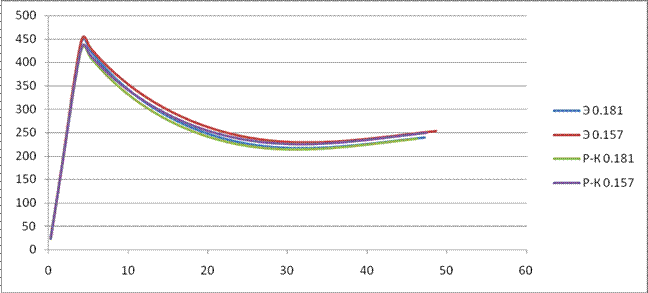
Сх=0.567
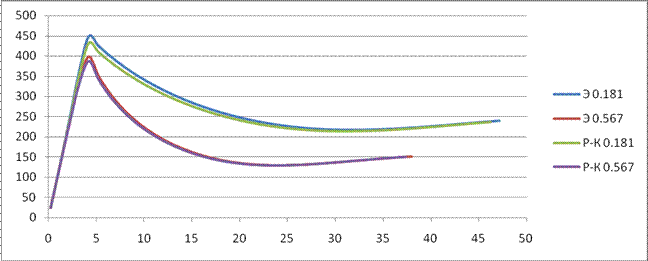
Q(t)
Cx=0.157
Сх=0.567
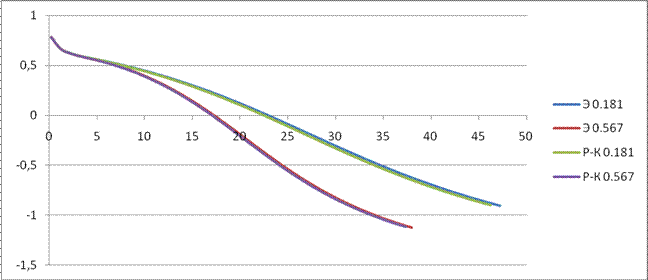
X(t):
Cx=0.157
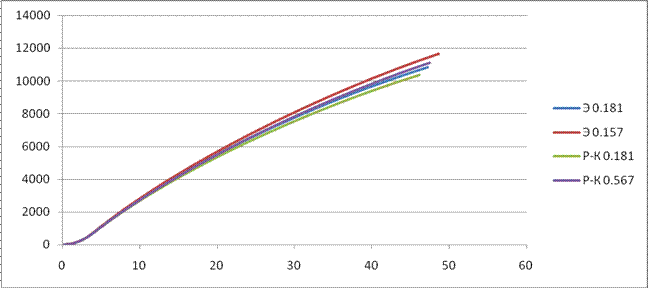
Сх=0.567
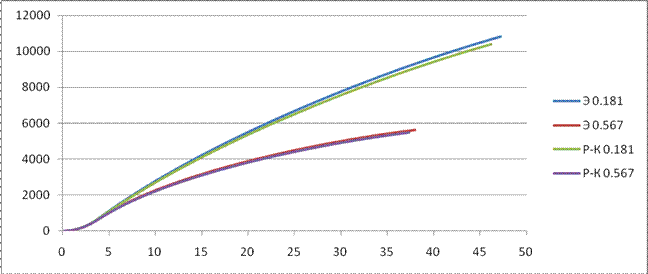
Y(t):
Cx=0.157
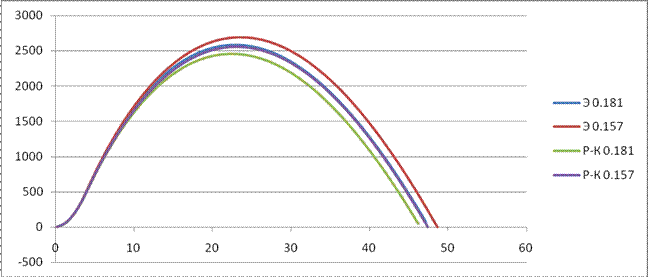
Сх=0.567
Приложение
Траектория неуправляемого летательного аппарата
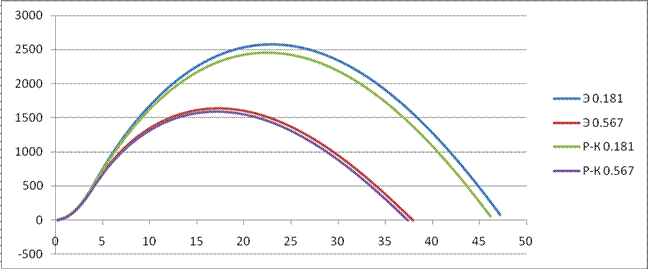
Зависимость y(t)
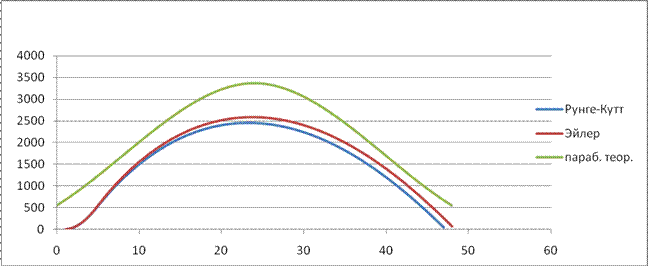
Зависимость x(t)
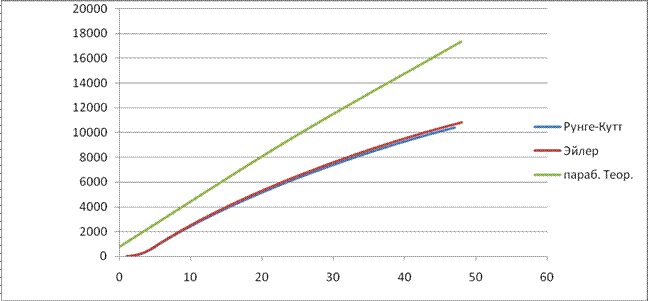
Зависимость v(t)
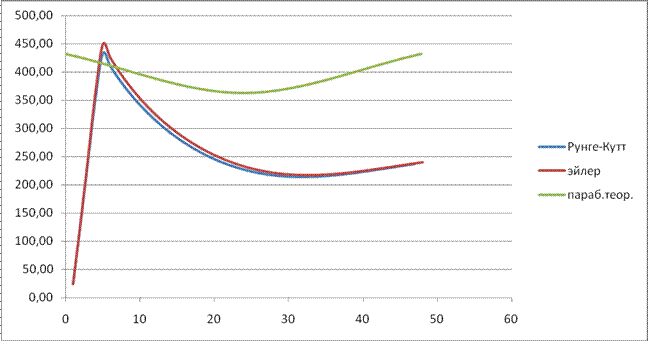
Зависимость угла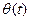 
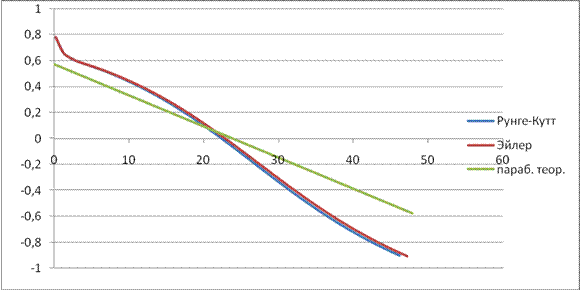
Зависимость y(x)
Программа расчета методом Рунге Кутта:
#include<stdio.h>
#include<math.h>
#include<conio.h>
#include<iostream.h>
#include<stdlib.h>
#include<dos.h>
main()
{
FILE *fin;
float t0,v0,y0,x0,dt,cx,i,ay1,ay2,ay3,ay4,r,ay11,ay22,ay33,ay44,
by1,by2,by3,by4,by11,by22,by33,by44,cy1,cy2,cy3,cy4,cy11,cy22,cy33,cy44,
dy1,dy2,dy3,dy4,dy11,dy22,dy33,dy44,q,q0,m,y111,y222,y333,s,y1,y2,y3,y4,w,w1,w2;
int k=1;
clrscr();
printf("PROGRAMMA RASCHOTA RUNGI-KUTT\n");
printf("Vvedite dt=");
scanf("%f",&dt);
printf("Vvedite t0=");
scanf("%f",&t0);
printf("Vvedite v0=");
scanf("%f",&v0);
printf("Vvedite y0=");
scanf("%f",&y0);
printf("Vvedite x0=");
scanf("%f",&x0);
printf("Vvedite cx=");
scanf("%f",&cx);
printf("Vvedite i=");
scanf("%f",&i);
printf("Vvedite q0=");
scanf("%f",&q0);
printf("Vvedite q=");
scanf("%f",&q);
printf("vvedite r=");
scanf("%f",&r);
printf("Vvedite s=");
scanf("%f",&s);
printf("Vvedite m=");
scanf("%f",&m);
printf("CHTOBU NACHAT RASCHOT NAGMITE 'ENTER'\n");
getch();
fin=fopen("RUNGIKUTT.txt","w+");
q0=((M_PI)*q0)/180;
w=m-q*t0; w1=m-q*(t0+dt);w2=m-q*(t0+(dt/2));
do{
if(t0>=2) w=w1=w2=m-q*2;
ay1=(r/w)-(0.5*i*cx*1.24*exp((-y0)/7800)*s*pow(v0,2))/w-9.81*sin(q0);
ay2=(-9.81*cos(q0))/v0;
ay3=v0*sin(q0);
w=m-q*(t0+dt);
by11=v0+ay1*(dt/2);
by22=q0+ay2*(dt/2);
by33=y0+ay3*(dt/2);
by1=(r/w2)-(0.5*i*cx*1.24*exp((-by33)/7800)*s*pow(by11,2)/w2)-9.81*sin(by22);
by2=(-9.81*cos(by22))/by11;
by3=by11*sin(by22);
cy11=v0+by1*(dt/2);
cy22=q0+by2*(dt/2);
cy33=y0+by3*(dt/2);
cy1=(r/w2)-((0.5*i*cx*1.24*exp((-cy33)/7800)*s*pow(cy11,2))/w2)-9.81*sin(cy22);
cy2=(-9.81*cos(cy22))/cy11;
cy3=cy11*sin(cy22);
w2=w2-q*(dt/2);
dy11=v0+cy1*(dt/2);
dy22=q0+cy2*(dt/2);
dy33=y0+cy3*(dt/2);
dy1=(r/w1)-(0.5*i*cx*1.24*exp((-dy33)/7800)*s*pow(dy11,2))/w1-9.81*sin(dy22);
dy2=(-9.81*cos(dy22))/dy11;
dy3=dy11*sin(dy22);
w1=w1-q*dt;
y111=(dt/6)*(ay1+2*(by1+cy1)+dy1);
y222=(dt/6)*(ay2+2*(by2+cy2)+dy2);
y333=(dt/6)*(ay3+2*(by3+cy3)+dy3);
y1=v0+y111;
y2=q0+y222;
y3=y0+y333;
y4=x0+(y333/tan(y2));
printf("v=%f\t",y1); printf("q=%f\t",y2); printf("x=%f\t",y4); printf("y=%f\t",y3);
if(k==1 || k%100==0)
{
fprintf(fin,"%f\t ",y1); fprintf(fin,"%f\t ",y2); fprintf(fin,"%f\t ",y4); fprintf(fin,"%f\t ",y3);
printf(fin,"%f\n ",t0);
}
t0=t0+dt;
if(t0>4)r=0;
v0=y1;
y0=y3;
x0=y4;
q0=y2;
if(t0<=4){ w=m-q*(t0+(dt/2)); w1=m-q*(t0+dt); }
if(t0>4)w1=w=m-q*4;
k++;
if(k==10000) break;
}
while(y3>0);
printf("\n");
printf("RASCHT ZAKONCHEN NAGMITE 'ENTER', FILE RUNGIKUTT.txt");
fclose(fin); getch(); return 0;
}
Промежуточные вычисления:
V: Q: Y: X: T:
23,763874 0,782398 1,932259 1,931275 0,220200
130,429199 0,665657 60,209183 50,639038 1,210199
240,823135 0,622026 209,025696 161,298325 2,210198
351,822113 0,594530 452,504089 330,191559 3,210197
432,421600 0,574160 789,378723 552,577148 4,210201
410,369293 0,554478 1145,322510 777,929565 5,210224
390,529816 0,533505 1487,881226 985,174377 6,210247
372,570251 0,511212 1818,487915 1175,542236 7,210270
356,230286 0,487569 2138,346680 1350,063477 8,210293
341,304321 0,462546 2448,473633 1509,606689 9,210316
327,628387 0,436118 2749,739258 1654,914673 10,210339
315,070465 0,408263 3042,888184 1786,622437 11,210361
303,524170 0,378962 3328,566406 1905,282227 12,210384
292,902863 0,348209 3607,338623 2011,374756 13,210407
283,135834 0,316002 3879,694092 2105,320312 14,210430
274,165192 0,282353 4146,065918 2187,491699 15,210453
265,943207 0,247286 4406,835449 2258,217773 16,210476
258,430359 0,210840 4662,344238 2317,796143 17,210499
251,593369 0,173071 4912,887695 2366,490967 18,210522
245,403946 0,134051 5158,762695 2404,544189 19,210545
239,837524 0,093874 5400,248047 2432,175537 20,210567
234,872025 0,052648 5637,703613 2449,588623 21,210590
230,487061 0,010502 5872,410156 2456,972656 22,210613
226,663147 -0,032420 6097,707520 2454,506836 23,210636
223,380859 -0,075957 6321,226074 2442,352783 24,210659
220,620346 -0,119939 6541,516113 2420,673584 25,210682
218,360825 -0,164188 6758,337891 2389,623779 26,210705
216,580521 -0,208521 6971,687012 2349,355713 27,210728
215,255966 -0,252755 7181,595215 2300,018311 28,210751
214,362350 -0,296715 7388,096680 2241,760742 29,210773
213,873505 -0,340230 7591,227539 2174,732422 30,210796
213,761581 -0,383144 7791,015137 2099,085938 31,210819
213,997803 -0,425316 7987,480469 2014,974976 32,210800
214,552155 -0,466622 8180,636230 1922,559082 33,210632
215,394058 -0,506956 8370,488281 1822,002563 34,210464
216,492340 -0,546230 8557,041992 1713,474976 35,210297
217,815765 -0,584377 8740,285156 1597,153198 36,210129
219,332977 -0,621347 8920,211914 1473,221069 37,209961
221,013184 -0,657105 9096,802734 1341,869263 38,209793
222,825775 -0,691633 9270,041992 1203,298706 39,209625
224,741074 -0,724925 9439,906250 1057,717041 40,209457
226,730392 -0,756987 9606,370117 905,341431 41,209290
228,765884 -0,787836 9769,406250 746,397583 42,209122
230,821045 -0,817495 9928,986328 581,120117 43,208954
232,870499 -0,845993 10085,081055 409,752747 44,208786
234,890274 -0,873367 10237,661133 232,547562 45,208618
236,857834 -0,899655 10386,698242 49,765450 46,208450
237,377380 -0,906571 10426,327148 -0,507259 46,488403
Программа расчёта методом Эйлера:
#include<stdio.h>
#include<math.h>
#include<conio.h>
#include<iostream.h>
#include<stdlib.h>
#include<dos.h>
main()
{
FILE *fin;
float t0,v0,y0,x0,dt,cx,i,r,s,q0,q,m,w,v1,x1,y1,q1,v11,x11,y11,q11;
int k=1;
clrscr();
printf("PROGRAMMA RASCHOTA EILERA\n");
printf("Vvedite dt=");
scanf("%f",&dt);
printf("Vvedite t0=");
scanf("%f",&t0);
printf("Vvedite v0=");
scanf("%f",&v0);
printf("Vvedite y0=");
scanf("%f",&y0);
printf("vvedite x0=");
scanf("%f",&x0);
printf("Vvedite cx=");
scanf("%f",&cx);
printf("Vvedite i=");
scanf("%f",&i);
printf("Vvedite q0=");
scanf("%f",&q0);
printf("Vvedite q=");
scanf("%f",&q);
printf("vvedite r=");
scanf("%f",&r);
printf("Vvedite s=");
scanf("%f",&s);
printf("Vvedite m=");
scanf("%f",&m);
printf("CHTOBU NACHAT RASCHOT NAGMITE 'ENTER'\n");
getch();
fin=fopen("EILER.txt","w+");
q0=((M_PI)*q0)/180;
w=m-q*t0;
do{
v11=r/w-((0.5*(cx*i*1.24*exp(-y0/7800)*s*pow(v0,2)))/w)-9.81*sin(q0);
q11=-9.81*cos(q0)/v0;
y11=v0*sin(q0);
x11=v0*cos(q0);
v1=v0+v11*dt;
q1=q0+q11*dt;
y1=y0+y11*dt;
x1=x0+x11*dt;
printf("v=%f\t",v1); printf("q=%f\t",q1); printf("y=%f\t",y1); printf("x=%f\t",x1);
if(k==1 || k%100==0)
{
fprintf(fin,"%f\t ",v1);
fprintf(fin,"%f\t ",q1); fprintf(fin,"%f\t ",x1); fprintf(fin,"%f\t ",y1); fprintf(fin,"%f\n ",t0);
}
t0=t0+dt;
if(t0>4)r=0;
v0=v1;
x0=x1;
y0=y1;
q0=q1;
if(t0<=4) w=m-q*(t0+dt);
if(t0>4) w=m-q*4;
k++;
if(k==10000) break;
}
while(y1>0);
printf("\n");
printf("RASCHT ZAKONCHEN NAGMITE 'ENTER', FILE EILER.txt");
fclose(fin);
getch();
return 0;
}
Промежуточные вычисления:
V: Q: X: Y: T:
23.763487 0.782344 1.928373 1.928373 0.220200
131.555527 0.664869 60.104259 50.557625 1.210199
245.423386 0.621682 210.645355 162.456131 2.210198
362.258942 0.594789 459.645721 335.258881 3.210197
448.610260 0.575086 807.672485 565.398193 4.210201
425.312317 0.556125 1176.425903 799.623352 5.210224
404.417419 0.535910 1530.832520 1015.116455 6.210247
385.550812 0.514415 1872.469849 1213.211670 7.210270
368.421021 0.491612 2202.653809 1395.019653 8.210293
352.798492 0.467472 2522.492676 1561.475098 9.210316
338.500519 0.441972 2832.930664 1713.372681 10.210339
325.380981 0.415087 3134.776855 1851.392578 11.210361
313.321747 0.386803 3428.725586 1976.120483 12.210384
302.226898 0.357106 3715.384766 2088.067139 13.210407
292.018005 0.325995 3995.277832 2187.680664 14.210430
282.631012 0.293475 4268.866699 2275.349854 15.210453
274.013245 0.259566 4536.555664 2351.424561 16.210476
266.120728 0.224298 4798.701172 2416.217041 17.210499
258.916901 0.187718 5055.616699 2470.004883 18.210522
252.370651 0.149888 5307.567383 2513.041016 19.210545
246.455460 0.110888 5554.813965 2545.554443 20.210567
241.147659 0.070814 5797.562500 2567.756836 21.210590
236.425873 0.029781 6036.002441 2579.842773 22.210613
232.269989 -0.012081 6270.298340 2581.993408 23.210636
228.660477 -0.054626 6500.593750 2574.381592 24.210659
225.577728 -0.097697 6727.014160 2557.172119 25.210682
223.001633 -0.141127 6949.667480 2530.521240 26.210705
220.911148 -0.184744 7168.646973 2494.581543 27.210728
219.283890 -0.228372 7384.031250 2449.501953 28.210751
218.096405 -0.271839 7595.883301 2395.431885 29.210773
217.323624 -0.314978 7804.257324 2332.520508 30.210796
216.939178 -0.357632 8009.194336 2260.917236 31.210819
216.915359 -0.399656 8210.727539 2180.774902 32.210800
217.223389 -0.440921 8408.875977 2092.249512 33.210632
217.833908 -0.481313 8603.659180 1995.501709 34.210464
218.716614 -0.520738 8795.081055 1890.696777 35.210297
219.840820 -0.559116 8983.143555 1778.006958 36.210129
221.175995 -0.596388 9167.840820 1657.611084 37.209961
222.691498 -0.632510 9349.162109 1529.694824 38.209793
224.357285 -0.667453 9527.090820 1394.452148 39.209625
226.143692 -0.701202 9701.610352 1252.085693 40.209457
228.021835 -0.733755 9872.696289 1102.805054 41.209290
229.963791 -0.765121 10040.324219 946.830811 42.209122
231.942581 -0.795314 10204.467773 784.390381 43.208954
233.932571 -0.824359 10365.097656 615.721252 44.208786
235.909058 -0.852286 10522.188477 441.068268 45.208618
237.848923 -0.879128 10675.707031 260.686157 46.208450
239.730392 -0.904923 10825.626953 74.837372 47.208282
Список использованных источников:
1. Шалыгин А.С. Основы статистической динамики летательных аппаратов: Учебное пособие – Л.: ЛМИ, 1989.
2. http://altfast.ru
3. http://www.belostokskaya.ru
4. http://www.narod.ru
5. http://www.rian.ru
6. http://www.vpk-news.ru
7. http://www.gunscity.ru
8. http://flot.sevastopol.info