Анализ характеристик корреляционной модели
Основными показателями, получаемыми в результате корреляционно-регрессионного анализа, являются коэффициенты регрессии и коэффициенты корреляции.
Анализ экономической интерпретации коэффициентов регрессии (параметров уравнения 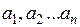 ) дает основание сформулировать общее определение его смысла. Коэффициент регрессии показывает, к какому изменению средней величины результативного признака приводит изменение факторного признака на одну единицу. Так, если при изучении корреляционной связи между урожайностью (У, ц/га) и дозами вносимых удобрений (Х, ц д.в. на 1 га) получено следующее уравнение регрессии:
) дает основание сформулировать общее определение его смысла. Коэффициент регрессии показывает, к какому изменению средней величины результативного признака приводит изменение факторного признака на одну единицу. Так, если при изучении корреляционной связи между урожайностью (У, ц/га) и дозами вносимых удобрений (Х, ц д.в. на 1 га) получено следующее уравнение регрессии:
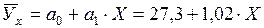 ,
,
Судя по уравнению, можно сказать следующее: увеличение внесения удобрений на одну единицу размерности (на 1 центнер) повлечет за собой изменение (в данном случае рост) урожайности на 1,02 ц/га, т.е. на величину коэффициента регрессии 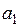 .
.
Таким образом, коэффициенты регрессии выступают в качестве показателей влияния или эффективности факторов.
Насколько правдоподобно коэффициенты регрессии отражают эффективность, отзывчивость факторов, зависит, правильно ли подобрана форма связи и какие факторы включены в модель.
Условный эффект фактора отражает коэффициент парной регрессии, т.е. в нашем примере коэффициент регрессии 1,02 характеризует влияние доз удобрений (чистое влияние) на урожайность и одновременно влияние других факторов, корреляционно связанных с дозами удобрений, и через этот фактор также влияющих на урожайность. Поэтому и считают, что коэффициент парной регрессии отражает условную эффективность фактора.
Чистую эффективность фактора может выражать коэффициент множественной регрессии при условии, что в подобранную модель включены все факторы, влияющие на анализируемый результативный признак. В этом случае влияние всех факторов выявляется в чистом виде, т.к. эффект каждого фактора «очищен» от влияния других, имеющих с ними корреляционную связь, ибо в уравнение включены все факторы.
Однако особенностью агроэкономических явлений является то, что в их формировании принимает участие чрезвычайно много факторов. Включить их все в одну модель практически невозможно. Поэтому различают относительно чистую эффективность коэффициентов множественной регрессии, которые получают в случае, когда в уравнение включены основные факторы, влияющие на результативный признак, и форма связи подобрана правильно. Каждый из коэффициентов такой модели характеризует не только «чистый» эффект фактора, но также и влияние корреляционно связанных с ним факторов, но не вошедших в данное уравнение регрессии. При этом каждый коэффициент регрессии «очищен» от влияния других факторов, входящих в уравнение регрессии. И чем правильнее и полнее выбраны и учтены основные наиболее существенные факторы, тем реальнее коэффициенты регрессии отражают чистую эффективность.
Для измерения тесноты связи между У и факторами, вошедшими в модель используют парные, частные и множественные коэффициенты корреляции. При линейной форме зависимости, показатели тесноты связи называют коэффициентами, при криволинейной – индексами. Линейные коэффициенты корреляции являются частным случаем индекса корреляции. Значение показателей тесноты связи в том, чтобы отразить, какую часть общей вариации результативного признака У можно объяснить независимым признаком Х, входящим в соответствующее уравнение регрессии. Измерение тесноты связи основано на сопоставлении показателей вариации результативного признака (У). Для этих целей исчисляют общую дисперсию
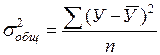 ,
,
характеризующую общую вариацию результативного признака (У), объясняемую влиянием всех факторов, от которых он зависит.
Факторную дисперсию исчисляют по формуле:
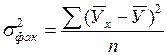 ,
,
которая характеризует вариацию (У), объясняемую только фактором (Х) или факторами ( 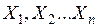 ), соответственно для парной и множественной корреляции.
), соответственно для парной и множественной корреляции.
В связи с этим для измерения тесноты связи используют отношение факторной дисперсии к общей дисперсии результативного признака. Это отношение называют индексом детерминации
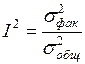 .
.
Корень квадратный из данного выражения называют индексом корреляции.
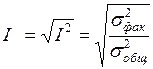 .
.
Подобно тому, как коэффициенты парной и множественной регрессии отражают условную и условно-чистую эффективность факторов, так парные и частные коэффициенты корреляции и детерминации характеризуют тесноту связи между (У) и факторами-аргументами ( 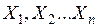 ), вошедшими в модель.
), вошедшими в модель.
Особо важное значение, имеет определение парных коэффициентов корреляции при отборе факторов. Для этого строится матрица парных коэффициентов корреляции, измеряющих тесноту линейной связи между результативным признаком (У) и каждым фактором-аргументом (Х), а также между факторами аргументами, т.е. между показателями 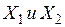 ,
, 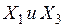 ,
, 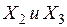 и т.д.
и т.д.
Таблица 15
