Образец выполнения лабораторной работы № 6

(Приближенное решение систем уравнений)

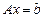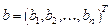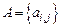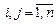Дана система линейных уравнений , где , , . Найти приближенное решение данной системы 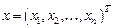с точностью .

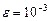Рассмотрим пример решения следующей системы уравнений

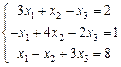, точное решение которой 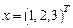, методами итераций и Зейделя.

1)Так как определитель системы 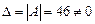, то система имеет единственное решение.

Приведем данную систему к виду 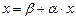, где

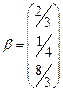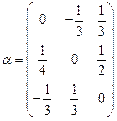, ; решение будем искать в виде итерационной последовательности , , .

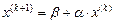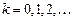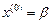Найдем канонические нормы матрицы .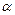

, , .

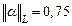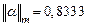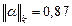Минимальной нормой является норма 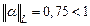. Поэтому все действия будем производить по этой норме. Итерационный процесс будем продолжать до тех пор, пока не будет выполняться условие

2) , .

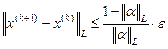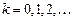А) По методу итерации получим , , .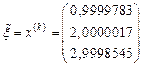

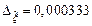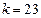Определим число верных знаков в приближенном значении решения. Так как 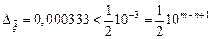, , 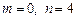то получим 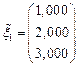с погрешностью округления 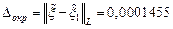. Тогда .

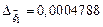Определим число верных знаков в приближенном решения 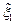. Так как 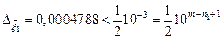, , 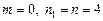то получим приближенное решение 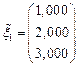, с погрешностью .

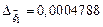Ответ: , .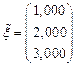

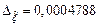Б) По методу Зейделя получим , , .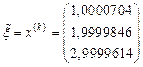

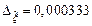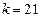Определим число верных знаков в приближенном значении решения. Так как 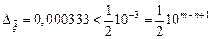, , 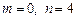то получим 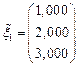с погрешностью округления 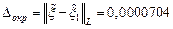. Тогда .

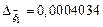Определим число верных знаков в приближенном решения 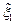. Так как 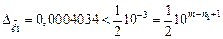, , 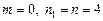то получим приближенное решение 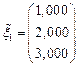,с погрешностью .

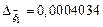Ответ: , .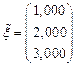

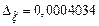Лабораторная работа № 7

Тема: Интерполирование функции. Полином Лагранжа.

Задание:

1)Найти приближенное значение функции при заданном значении аргумента 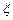с помощью интерполяционного полинома Лагранжа, если функция задана в не равноотстоящих узлах;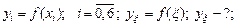

2)Оценить погрешность полученного значения.

Вопросы самоконтроля.

1) Постановка задачи интерполирования. Геометрическая иллюстрация.

2) В чем различие между задачами интерполяции и задачами экстраполяции?

3) Привести формулу Лагранжа. Дать оценку погрешности.

4) Как выглядит формула Лагранжа для равностоящих узлов?

5) От чего зависит точность получаемого формулой Лагранжа результата?

6) Когда полином m порядка будет аппроксимировать формулой Лагранжа с наименьшей погрешностью?