Теорема Больцано-Вейерштарсса

Теорема 6. (Больцано-Вейерштрасса). Из всякой ограниченной последовательности можно извлечь сходящуюся подпоследовательность. Доказательство. Пусть X – множество значений ограниченной последовательности {x_n}. Если X конечное множество, то тогда очевидно найдется a ∈ X который будет повторяться в последовательности бесконечное число раз. Пусть он повторяется под номерами n₁ < n₂ < . . . < n_k < . . . Тогда последовательность {x_nk} постоянна т.к. x_nk = a, ∀ k ∈ 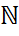и значит сходится. Если X бесконечно, то согласно лемме 5 оно обладает по крайней мере одной предельной точкой a. Поскольку a –предельная точка множества X то можно выбрать n₁ ∈ 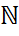так, что |x_n1 − a| <1. 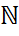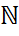Если n_k ∈ уже выбрано так, что |x_nk−a| < , то учитывая, что a предельная точка множества X, найдем n_k+1 ∈ так, что n_k < n_k+1 и |x_nk+1−a| < 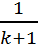. Поскольку 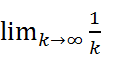=0, то построенная подпоследовательность x_n1 , x_n2 , . . . , x_nk , . . . сходится к a.

Замечание 1. Мы имеем, что всякая сходящаяся подпоследовательность ограничена, обратное вообще говоря неверно,например, x_n = (−1)ⁿ. Однако для ограниченной последовательности имеет место указанная выше теорема.

Предел функции.

Пусть функция f(x) определена в проколотой окрестности точки x₀ т.е. на множестве _δ(x₀)= {x : 0 < |x−x₀| < δ}. В точке x₀ значение f(x₀) может быть не определено. Определение 1 (по Коши, или, на языке «ε − δ» ). Число y₀ называется пределом функции y = f(x) в точке x₀ (или, при x → x₀), если для любого ε > 0 можно указать такое число δ = δ(ε) > 0, что при всех x, удовлетворяющих условию 0 < |x − x₀| < δ, выполняется неравенство |f(x) − y₀| < ε, или: y₀= 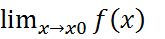⇔ ∀ε > 0 ∃δ > 0 : ∀x 0 < |x − x₀| < δ ⇒ |f(x) − y0| < ε . В определении 1 используются понятия ε-окрестности и проколотой δ-окрестности. Если обозначить V_ε(y₀) = {y = f(x) : |f(x) − y₀| < ε}, 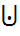_δ(x₀) = {x : 0 < |x − x₀| < δ}, то его кратко записывают еще в виде y₀= 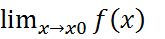⇔ ∀ε > 0 ∃δ > 0 ∀x ∈ 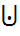_δ(x₀) ⇒ f(x) ∈ V_ε(y₀). Определение 2 (по Гейне, или, на языке последо-вательностей). Число y₀ называется пределом функции y = f(x) в точке x₀ (или, при x → x₀), если для любой последовательности точек x_n ∈ 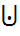_δ(x₀), сходящейся к x₀, последовательность соответствующих значений функции f(x_n) сходится к y₀: y₀= 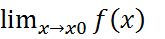⇔ ∀x_n : 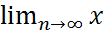_n=x₀⇒ 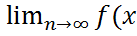_n) = y_{0 .}Св-ва:

Определение 3. Функция f : X → R называется финально постоянной при X 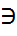x → x₀, если она постоянна в некоторой проколотой окрестности 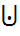_δ(x₀) точки x₀, предельной для множества X. Определение 4. Функция f : X → R называется финально-ограниченной при X 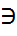x → x₀ если существует 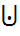_δ(x₀), что

∀x ∈ 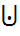_δ(x₀) будет |f(x)| < M, где M > 0.

Теорема 8. а) Если y₀ предел функции f(x) при x → x₀, то f(x) финально ограничена при x → x₀; б) Если f(x) финально постоянна при x → x₀ то она имеет предел в точке x₀; в) Если f(x) в точке x₀ имеет предел, то этот предел единственный. Доказательство. Утверждение а) о финальной ограниченности функции имеющей предел и утверждение б) о наличии предела у финально постоянной функции, вытекает прямо из соответствующих определений. Докажем единственность предела. Предположим противное, т.е. пусть в точке x₀ функция f(x) имеет два предела y0 и y1, и при этом y₀ 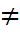y₁, т.е. y₀= 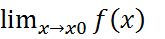⇔ ∀ε > 0 ∃δ₁ > 0 : ∀x 0 < |x − x₀| < δ₁⇒ |f(x) − y₀| < . и y₁= 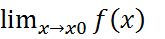⇔ ∀ε > 0 ∃δ₂ > 0 : ∀x 0 < |x − x₀| < δ₂⇒ |f(x) – y₁| < .Тогда ∀x ∈ 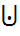_δ(x₀), где δ = min{δ₁, δ₂} имеем 0 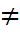|y₀ − y₁| 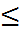|y₀ − f(x)| + |f(x) − y₁| < + 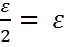что противоречит предположению.