Доверительный интервал дисперсии нормального распределения
Пусть случайная величина x распределена по нормальному закону, для которого дисперсия Dx неизвестна. Делается выборка объема n . Из нее определяется исправленная выборочная дисперсия s2. Случайная величина
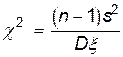 (10.2.8)
(10.2.8)
распределена по закону c2 c n –1 степенями свободы. По заданной надежности g можно найти сколько угодно границ c12 и c22 интервалов, таких, что
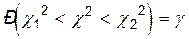 (10.2.9)
(10.2.9)
Найдем c12 и c22 из следующих условий:
P(c2 £ c12) = (1 – g )/ 2 (10.2.10)
P(c2 ³ c22) = (1 – g )/ 2 (10.2.11)
Очевидно, что при выполнении двух последних условий справедливо равенство (10.2.9).
В таблицах для случайной величины c2 обычно дается решение уравнения P(c2 ³cq2) = q . Из такой таблицы по заданной величине q и по числу степеней свободы n – 1 можно определить значение cq2. Таким образом, сразу находится значение c22 в формуле (10.2.11).
Для определения c12 преобразуем (10.2.10):
P(c2 ³ c12) = 1 – (1 – g )/ 2 = (1 + g )/ 2
Полученное равенство позволяет определить по таблице значение c12.
Теперь, когда найдены значения c12 и c22, представим равенство (10.2.9) в виде
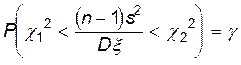 .
.
Последнее равенство перепишем в такой форме, чтобы были определены границы доверительного интервала для неизвестной
величины Dx:
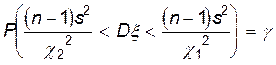 .
.
Отсюда легко получить формулу, по которой находится доверительный интервал для стандартного отклонения:
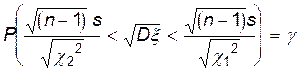 (10.2.12)
(10.2.12)
Задача. Будем считать, что шум в кабинах вертолетов одного и того же типа при работающих в определенном режиме двигателях — случайная величина, распределенная по нормальному закону. Было случайным образом выбрано 20 вертолетов, и произведены замеры уровня шума (в децибелах) в каждом из них. Исправленная выборочная дисперсия измерений оказалась равной 22,5. Найти доверительный интервал, накрывающий неизвестное стандартное отклонение величины шума в кабинах вертолетов данного типа с надежностью 98%.
Решение. По числу степеней свободы, равному 19, и по вероятности (1 – 0,98)/2 = 0,01 находим из таблицы распределения c2величину
c22 = 36,2. Аналогичным образом при вероятности (1 + 0,98)/2 = 0,99 получаем c12 = 7,63. Используя формулу (10.2.12), получаем искомый доверительный интервал: (3,44; 7,49).
Тема 10.3. Задачи статистической проверки гипотез
Основные понятия и статистическая проверка гипотез
Статистическая проверка гипотез является вторым после статистического оценивания параметров распределения и в то же время важнейшим разделом математической статистики.
Методы математической статистики позволяют проверить предположения о законе распределения некоторой случайной величины (генеральной совокупности), о значениях параметров этого закона (например Mx, Dx ), о наличии корреляционной зависимости между случайными величинами, определенными на множестве объектов одной и той же генеральной совокупности.
Пусть по некоторым данным имеются основания выдвинуть предположения о законе распределения или о параметре закона распределения случайной величины (или генеральной совокупности, на множестве объектов которой определена эта случайная величина). Задача заключается в том, чтобы подтвердить или опровергнуть это предположение, используя выборочные (экспериментальные) данные.
Гипотезы о значениях параметров распределения или о сравнительной величине параметров двух распределений называются параметрическими гипотезами.
Гипотезы о виде распределения называются непараметрическими гипотезами.
Проверить статистическую гипотезу – это значит проверить, согласуются ли данные, полученные из выборки с этой гипотезой. Проверка осуществляется с помощью статистического критерия. Статистический критерий – это случайная величина, закон распределения которой (вместе со значениями параметров) известен в случае, если принятая гипотеза справедлива. Этот критерий называют еще критерием согласия (имеется в виду согласие принятой гипотезы с результатами, полученными из выборки).
Гипотезу, выдвинутую для проверки ее согласия с выборочными данными, называют нулевой гипотезойи обозначают H0. Вместе с гипотезой H0 выдвигается альтернативная или конкурирующаягипотеза, которая обозначается H1. Например:
| 1) | H0: Mx= 0 | 2) | H0: Mx= 0 | 3) | H0: Mx= 0 |
| H1: Mx¹ 0 | H1: Mx> 0 | H1: Mx= 2 |
Пусть случайная величина K – статистический критерий проверки некоторой гипотезы H0. При справедливости гипотезы H0 закон распределения случайной величины K характеризуется некоторой известной нам плотностью распределения pK(x).
Выберем некоторую малую вероятность a, равную 0,05 , 0,01 или еще меньшую. Определим критическое значение критерия Kкр как решение одного из трех уравнений, в зависимости от вида нулевой и конкурирующей гипотез:
P(K> Kкр) = a (10.3.1)
P(K< Kкр) = a (10.3.2)
P((K< Kкр1)Ç(K> Kкр2)) = a (10.3.3)
Возможны и другие уравнения, но они встречаются значительно реже, чем приведенные.
Решение уравнения (10.3.1) (то же самое для уравнений (10.3.2) и (10.3.3)) заключается в следующем: по вероятности a, зная функцию pK(x), заданную как правило таблицей, нужно определить Kкр.
Что означает условие (10.3.1)?
Если гипотеза H0 справедлива, то вероятность того, что критерий K превзойдет некоторое значение Kкр очень мала – 0,05 , 0,01 или еще меньше, в зависимости от нашего выбора. Если Kв – значение критерия K, рассчитанное по выборочным данным, превзошло значение Kкр, это означает, что выборочные данные не дают основания для принятия нулевой гипотезы H0 ( например, если a=0,01 , то можно сказать, что произошло событие, которое при справедливости гипотезы H0 встречается в среднем не чаще, чем в одной из ста выборок). В этом случае говорят, что гипотеза H0 не согласуется с выборочными данными и должна быть отвергнута. Если Kв не превосходит Kкр, то говорят, что выборочные данные не противоречат гипотезе H0, и нет оснований отвергать эту гипотезу.
Для уравнения (10.3.1) область K> Kкр называется критической областью. Если значение Kв попадает в критическую область, то гипотеза H0 отвергается.
Для уравнения (10.3.1) область K < Kкр называется областью принятия гипотезы. Если значение Kв попадает в область принятия гипотезы, то гипотеза H0 принимается.
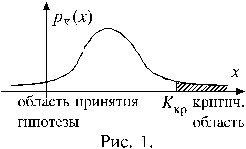 |
Рисунок 1. иллюстрирует решение уравнения (10.3.1). Здесь pK(x) – известная плотность распределения случайной величины K при условии справедливости гипотезы H0.
Пусть выбрано некоторое малое значение вероятности a, по нему определено значение Kкр и по выборочным данным определено значение Kв, которое попало в критическую область. В этом случае гипотеза H0 отвергается, но она может оказаться справедливой, просто случайно произошло событие, которое имеет очень малую вероятность a. В этом смысле a есть вероятность отвержения правильной гипотезы H0.
Отвержение правильной гипотезы называется ошибкой первого рода. Вероятность a называется уровнем значимости. Таким образом уровень значимости – это вероятность совершения ошибки первого рода.
 |
Критическая область, полученная для уравнения (10.3.1) и приведенная на рисунке 1., называется правосторонней.
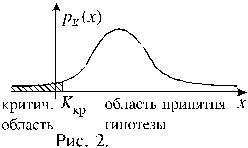
Уравнение (10.3.2) определяет левосторонюю критическую область. Ее изображение приводится на рисунке 2.
 |
Отметим, что каждая из заштрихованных фигур на рисунках 1 и 2 имеет площадь, равную a.
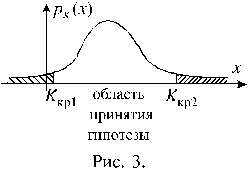
Уравнение (10.3.3) определяет двусторонюю критическую область. Такая область изображена на рисунке 3. Здесь критическая область состоит из двух частей. В случае двусторонней критической области границы ее частей Kкр1 и Kкр2 определяются таким образом, чтобы выполнялось условие:
P(K £ Kкр) = P(K ³ Kкр) = a / 2.
На рисунке 3. площадь каждой из заштрихованных фигур равна a / 2.
Вид критической области зависит от того, какая гипотеза выдвинута в качестве конкурирующей.
Чем меньше уровень значимости, тем меньше вероятность отвергнуть проверяемую гипотезу H0, когда она верна, то есть совершить ошибку первого рода. Но с уменьшением уровня значимости расширяется область принятия гипотезы H0 и увеличивается вероятность принятия проверяемой гипотезы, когда она неверна, то есть когда предпочтение должно быть отдано конкурирующей гипотезе.
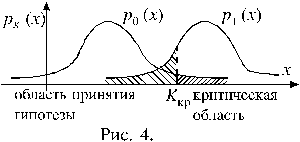
Пусть при справедливости гипотезы H0 статистический критерий K имеет плотность распределения p0(x), а при справедливости конкурирующей гипотезы H1 – плотность распределения p1(x). Графики этих функций приведены на рисунке 4. При некотором уровне значимости находится критическое значение Kкр и правосторонняя критическая область. Если значение Kв, определенное по выборочным данным, оказывается меньше, чем Kкр, то гипотеза H0 принимается. Предположим, что справедлива на самом деле конкурирующая гипотеза H1. Тогда вероятность попадания критерия в область принятия гипотезы H0 есть некоторое число b, равное площади фигуры, образованной графиком функции p1(x) и полубесконечной частью горизонтальной координатной оси, лежащей слева от точки Kкр. Очевидно, что b – это вероятность того, что будет принята неверная гипотеза H0.
Принятие неверной гипотезы называется ошибкой второго рода. В рассмотренном случае число b – это вероятность ошибки второго рода. Число 1 – b, равное вероятности того, что не совершается ошибка второго рода, называется мощностью критерия. На рисунке 4 мощность критерия равна площади фигуры, образованной графиком функции p1(x).и полубесконечной частью горизонтальной координатной оси, лежащей справа от точки Kкр.
Выбор статистического критерия и вида критической области осуществляется таким образом, чтобы мощность критерия была максимальной.
 |
