Колебания тела на пружине. Уравнение малых колебаний
Изучение колебаний математического маятника
Методические указания к выполнению лабораторной работы
ЕТИ. Ф.ЛР.04.
г. Егорьевск 2014
Составители: _____________ В.Ю. Никифоров, ст. преподаватель ЕНД
В методических указаниях рассмотрены: понятие колебания тела и его характеристики, гармонические колебания и понятие гармонического осциллятора, изучение свободных колебаний маятника, с хорошей точностью удовлетворяющего модели математического маятника; оценка точности реализации этой модели в лабораторной установке; определение ускорения свободного падения с помощью математического маятника; оценка результатов измерений и расчет погрешностей.
Методические указания предназначены для студентов 1 курса, обучающихся по направлению подготовки бакалавров 280700 Техносферная безопасность для лабораторных работ по дисциплине "Физика".
Методические указания обсуждены и одобрены на заседании учебно-методической группы (УМГ) кафедры ЕНД
(протокол № ___________ от __________г.)
Председатель УМГ _____________ Г.Г Шабаева
Изучение колебаний математического маятника
1 Цель работы:изучение свободных колебаний маятника, с хорошей точностью удовлетворяющего модели математического маятника; оценка точности реализации этой модели в лабораторной установке; определение ускорения свободного падения; оценка результатов измерений и расчет погрешностей.
2 Оборудование:лабораторная установка, метровая линейка, электронный секундомер
Содержание работы
3.1 Изучить теоретический материал.
3.2 Проверить изохронность колебаний маятника. Определить период колебаний для 8—10 значений амплитуды θ в пределах от 0 до 30°.
3.3 Оценить влияние затухания на период колебаний. С этой целью определить число колебаний N, за которое амплитуда колебаний уменьшается примерно в три раза.
3.4 Определить с помощью микрокалькулятора значение наименьшей длины подвеса маятника аmin, при которой с точностью до 0,5% можно считать момент инерции маятника равным 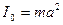 . Для этого в соотношении (25) примите ΔIсист/I0 = 0,005 и вычислите аmin.
. Для этого в соотношении (25) примите ΔIсист/I0 = 0,005 и вычислите аmin.
3.5 Провести экспериментальную проверку линейной зависимости между квадратом периода колебаний Т2 и длиной а подвеса. Провести измерение периода колебаний Т для выбранных значений a. Результаты измерений занести в таблицу 2.
3.6 Построить по точкам график полученной экспериментально зависимости Т2 от а в осях координат X = а, Y = Т2.
3.7 Определить ускорение свободного падения g. Вычислить g с помощью формулы (28) при найденных значениях Т и а.
3.8 Оценить погрешность 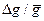 . Сделать вывод.
. Сделать вывод.
3.9 Оформить отчет.
Теоретические сведения к работе
Колебания тела на пружине. Уравнение малых колебаний
Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из состояния равновесия. Примером свободных колебаний могут служить колебания груза на пружине.
Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению х тела из положения равновесия.
Этому условию удовлетворяет упругая сила пружины Fх=-kx. Коэффициент k называется жесткостью пружины. Все другие силы, удовлетворяющие этому условию, называются квазиупругими.
Если тело, прикрепленное к упругой пружине, вывести из состояния равновесия, то на тело начнет действовать упругая сила со стороны пружины, которая по закону Гука пропорциональна отклонению тела от положения равновесия. Следует помнить, что закон Гука справедлив только для малых отклонений от положения равновесия (количественно это выражается неравенством x << l, где l – длина нерастянутой пружины, х - удлинение пружины).
Уравнение движения под действием упругой силы имеет вид:
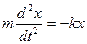 (1)
(1)
Его можно переписать в другой форме, введя обозначение ω2 = k/m. Тогда
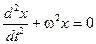 (2)
(2)
Система, совершающая колебания, описываемые этим уравнением, называется гармоническим осциллятором. Величина ω называется собственной круговой частотой колебаний. Для груза на пружине
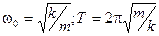 ; (3)
; (3)
Гармонические колебания происходят по закону
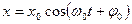 , (4)
, (4)
где x0 и φ0 - амплитуда и начальная фаза колебаний. Эти величины зависят от начальных условий.
При гармонических колебаниях кинетическая и потенциальная энергия периодически изменяются, но полная механическая энергия Е замкнутой системы, в которой отсутствуют силы сопротивления, остается неизменной.
Для груза на пружине
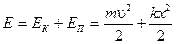 ;
; 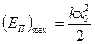 ; (5)
; (5)
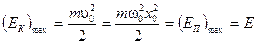 (6)
(6)
При гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот.
При наличии сил трения (сопротивления) полная энергия системы уменьшается со временем, и колебания становятся затухающими.
Если сила сопротивления пропорциональна скорости (вязкое трение) Fтр= - bυ, амплитуда колебаний А уменьшается по закону
A = x0e-δt, где δ=b/2m (7)
Постоянная δ называется коэффициентом затухания. Интервал времени τ = 1/δ, в течение которого амплитуда уменьшается в e≈2,7 раза, называется временем затухания.
