Указания по выполнению работы

Пример 1.Для исследования устойчивости САУ по критерию Найквиста необходимо рассчитать и построить амплитудно-фазовую частотную характеристику (АФЧХ) исходной разомкнутой САУ.

Рисунок 10.13 Структурная схема системы

В соответствии со структурной схемой (рис.10..) передаточную функцию разомкнутой САУ можно представить в виде произведения передаточных функций динамических звеньев:

интегрирующего звена с передаточной функцией

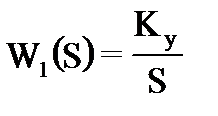(10.11)

апериодическогозвена первого порядка с передаточной функцией

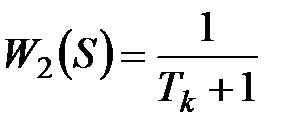(10.12)

колебательного звена с передаточной функцией

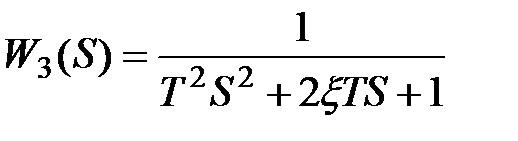(10.13)

Получаем

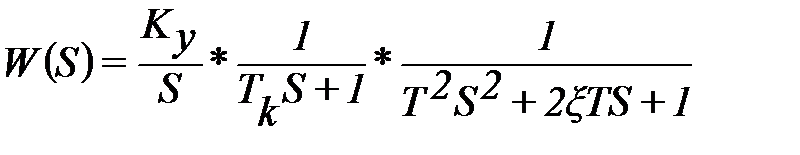(10.14)

Тогда комплексная передаточная функция W(јω) имеет вид(вместо Sподставляем јω):

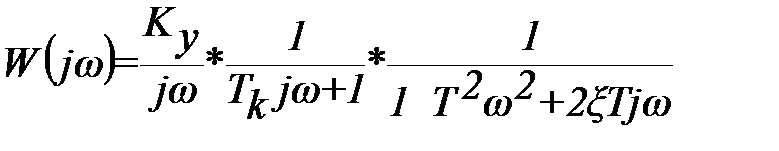(10.15)

В этом случае расчет АФЧХ проще всего производить следующим образом: задавшись конкретным значением частоты, определяем модуль и аргумент для каждого звена. Далее необходимо определить модуль и аргумент всей системы, учитывая, что результирующий модуль будет равен произведению модулей отдельных звеньев, а результирующий аргумент алгебраической сумме аргументов отдельных звеньев. Аналогичным образом производится расчет для остальных точек (значений частоты), число которых выбирается равным 10-15.

Весь расчет целесообразно свести в таблицу. Передаточной функции (10.15) соответствует таблица 10.1

Таблица 10.1 -Расчет АФЧХ разомкнутой САУ

Звенья

Частота ω, с-1

W1(jω)

A1(ω)

φ1(ω)

W2(jω)

A2(ω)

φ2(ω)

W3(j ω)

A3(ω)

φ3(ω)

A(ω)= A1(ω)* A2(ω)* A3(ω)

φ(ω)= φ1(ω)+ φ2(ω)+ φ3(ω)

По данным таблицы строится АФЧХ исходной разомкнутой САУ и исследуется ее устойчивость по критерию Найквиста. В случае устойчивой САУ необходимо определить запасы устойчивости по фазе и амплитуде.

Пример 10.2 Расчет устойчивости систем по критерию Найквиста. Рассчитать устойчивость системы, заданной следующей структурной схемой (рис 10.14.) .

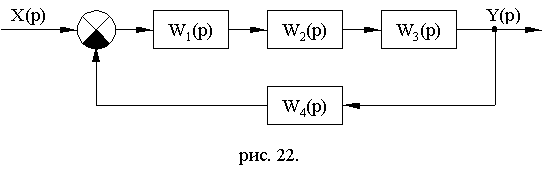
Рис. 10.14

W₁(P)=k₁; W₂(P)= 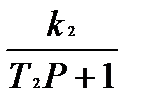;W₃(P)= 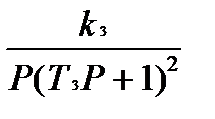; W₄(P)= .

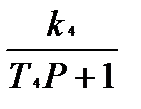Параметры звеньев: k₁=12; k₂=80; k₃=0.15; k₄=2; T₂=0.5; T₃=10; T₄=2.

Запишем эквивалентную передаточную функцию системы

W_зам(р) = .

Запишем передаточную функцию системы, разомкнутой по главной обратной связи.

W_раз(p) = W₁(P) ×W₂(P) ×W₃(P) ×W₄(P) = .

Характеристическое уравнение системы.

D(p)=1+ W_раз(p)=0 ® D(p)=1+ = 0;

K_э+(Т₂Т₃р³+Т₂р²+Т₄р+р)(Т₃²р²+2Т₃р+1)=0; Kэ=К₁К₂К₃К₄;

K_э + Т₂Т₄Т₃² р⁵ + (2Т₂Т₄Т₃ + Т₂Т₃² + Т₄Т₃²) р⁴ + (Т₄Т₂ + 2Т₂Т₃ + 2Т₄Т₃ + Т₃²) р³ +
(Т₂ + Т₄ + 2Т₃) р² + р = 0 ® .

Подставляя численные значения, получаем:

.

Критерий Найквиста.

Определяем устойчивость по АФЧХ системы, разомкнутой по главной обратной связи.

W_раз(p)= W₁(P)* W₂(P)* W₃(P) * W₄(P)= .

Комплексный коэффициент передачи САУ получим, заменяя p®jw

W_раз(jw)= .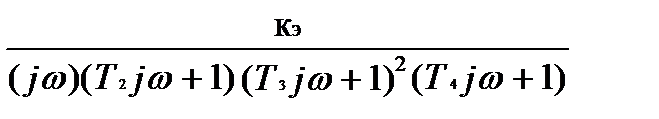

Выведем действительную и мнимую части домножая числитель и знаменатель на комплексно-сопряженные множители.

;

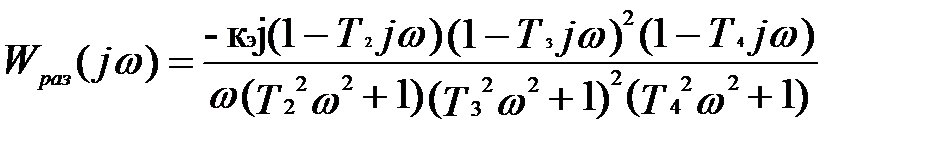Re= ;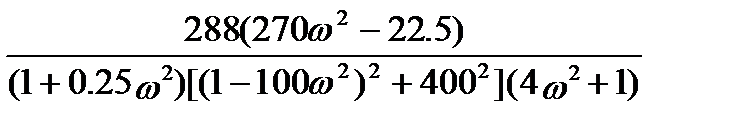
Im= .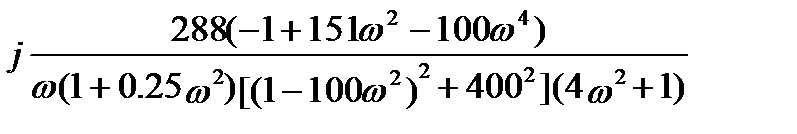

Задаваясь значениями w из промежутка 0 £ w < ¥, рассчитываем Re(w) и Im(w).

Таблица 2

w		0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9		¥
Re	-6336	-1334	-115	3,72	12,4	9,1	5,95	3,8	2,5	1,65	0,056
Im	-¥					12,2	5,33	2,43	1,13	0,52	-0,026

По данным таблицы строим АФЧХ системы (рис. 10.15).

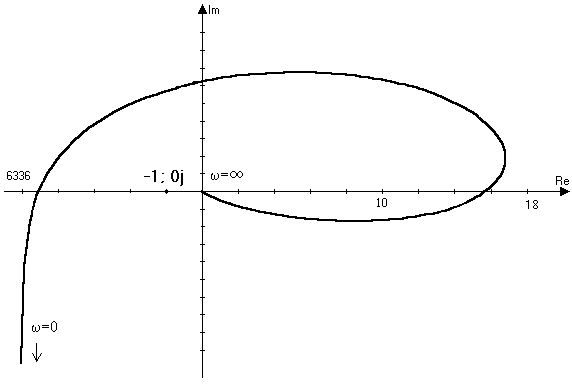
Рис. 10.15

Система неустойчива т.к. при дополнении годографа дугой с бесконечным радиусом до положительного отрезка вещественной оси АФЧХ охватывает критическую точку с координатами (–1; 0j).