В. Порядок операций при обработке результатов косвенных измерений

1. Заносят в таблицу результаты всех прямых наблюдений величин , , и инструментальные погрешности , , , через которые выражается косвенно определяемая величина 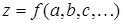, а также результаты последующих расчетов.

2. В соответствии с п.п. З–7 (см. стр.14) включительно обрабатывают результаты всех прямых многократных измерений величин 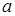, , 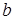,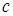..., после чего записывают

, , , (22)

находят , рассчитывают

, , . (23)

Примечание. Числа наблюдений , , ,... величин 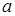, , 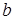,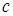... следует брать одинаковыми, так как при разных , , ,... теряют смысл доверительные границы косвенно определяемой величины (даже при одной и той же доверительной вероятности для 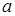, , 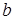,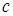... и т.д.).

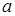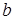В связи с этим в случае обнаружения грубой погрешности даже одной из наблюдаемых величин ( или , или 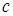,...) исключают все результаты наблюдении данного опыта и заменяют их новыми. Например, пусть в одном из опытов с маховым колесом мы измерили высоты , и время и оказалось, что приводит к грубой погрешности . В таком случае , и следует вычеркнуть из результатов наблюдений, сделать дополнительный опыт и заменить , и новыми результатами , и не ведущими к грубым погрешностям, чтобы сохранить .

3. Задаваясь для всех величин 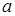, , 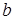,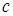... одним и тем же значением доверительной вероятности, находят величины, определяющие доверительные границы для , , ,...:

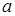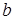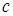, , (24)

4. С учетом инструментальных погрешностей , , ,... рассчитывают абсолютные погрешности, обусловленные только "а", только "в", только "с" и т.д. - полные погрешности

(25)

5. Находят для конкретной лабораторной работы выражения для расчета абсолютных погрешностей 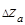, , 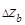,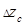... например, по методу частных дифференциалов и с помощью формулы (19) рассчитывают доверительные границы результата косвенных измерений

. (26)

Примечание. Всеми погрешностями (в случае ), которые составляют от максимальной из величин 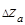, , 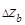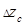и т.д., не являющейся грубой погрешностью, долю , пренебрегают, так как их вклад в полную погрешность мал.

6. Окончательный результат косвенных измерений представляют в виде:

, при , , (27)

подставляя соответствующие численные значения и указывая единицы их измерения.

Б. Пример. Найти с помощью дифракционной решетки длину световой волны и ее абсолютную погрешность .

1. Записываем инструментальные погрешности и результаты наблюдений:

постоянная дифракционной решетки , , инструментальная погрешность (малого) гониометра ;

результаты прямых наблюдений углов для желтой линии ртутной лампы:

№ опыта	Порядок максимума	лев.	прав.

Находим среднее значение и а также абсолютные погрешности отдельных наблюдений:

,

, , , , , .

Тогда .

Очевидно, среди грубых погрешностей нет. Кроме того, , так как имеет лишь одно числовое значение.

Рассчитываем: .

2. Находим .

3. Задаемся доверительной вероятностью 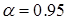(только для определения величины , так как ) и для находим по табл. величину коэффициента Стьюдента .

Это дает: .

4. В итоге полная погрешность определения величины :

.

5. Находим выражение для расчета абсолютных погрешностей и , обусловленных соответственно и : .

Тогда по методу частных дифференциалов:

, откуда .

, откуда .

Следовательно, полная погрешность .

Но , , , , .

Это дает .

Таким образом, .

Поэтому .

6. Окончательный результат косвенных измерений величины с помощью дифракционной решетки записываем в виде:

, ,

при , .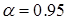

Таблица коэффициентов Стьюдента для .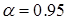

n
tα	12,71	4,30	3,18	2,78	2,57	2,45	2,36	2,31	2,26	2,23

Приложение 2. УКАЗАНИЯ ПО ВЫЧИСЛЕНИЮ И КРУГЛЕНИЮ РЕЗУЛЬТАТОВ ВЫЧИСЛЕНИЙ И ПРАВИЛА ПОСТРОЕНИЯ ГРАФИКОВ

1. Точность вычислений и численного значения постоянных величин

Точность вычислений и численного значения постоянных величин, используемых в расчетах, должна быть такой, чтобы не увеличивать погрешностей, обусловленных наблюдениями и приборами. Для этого необходимо соблюдать следующие правила.

Точность расчетов должна быть на порядок выше, чем результатов наблюдении.

Примечание: большая точность вычислений не имеет смысла, так как она в принципе не может уменьшить экспериментальные погрешности.

Погрешность, с которой следует брать универсальные постоянные, иррациональные числа и т.д., определяется тем же условием: ошибка, вносимая их округлением, должна быть приблизительно на порядок меньше погрешностей опыта.

Точность задания постоянных величин, используемых в данной работе (масс тел, радиусов шкивов, постоянной дифракционной решетки и т.д.), приведенных в методических указаниях или на лабораторных установках, тоже должна подчиняться этим требованиям.

Если точность постоянных не задана, то погрешность соответствующей величины берется как половина единицы последнего приводимого десятичного разряда. Так, например, если на установке приведена масса в 45,37 г., то ;

если постоянная дифракционной решетки , то и т.д.

Если округляемая значащая цифра , то ее отбрасывают, если же она , то цифру предыдущего десятичного разряда увеличивает на единицу. Так, например, если в результате расчета мы получим число , то его следует округлить до ; а если получено число , то до .

2. Округление погрешностей

При числе наблюдений округление полных погрешностей выполняют по следующим правилам.

Погрешности следует вычислять с точностью, на порядок большей точности наблюдений.

Погрешности округляют. Пусть, например, в результате двух серий измерений получены следующие средние погрешности:

и .

После округления приводят только первую значащую цифру, если она больше трех. Это, очевидно, относится к , вместо которого после округления следует принять . После округления приводят первые две цифры, если первая из них меньше трех или равна трем. Это относится к результату , который после округления следует записать в виде .

Искомые величины также надо округлять до того же порядка, что и погрешность. Так, если , то в случае результат следует записать в виде:

, а в случае как .

Примечание: значок показывает одинаковый разряд, до которого выполнено округление и в , и в .

Пример. Пусть необходимо найти косвенно определяемую величину - объем шарика - за счет прямых измерений его диаметра , причем в результате расчета уже получены и при .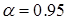

Найдем выражение для расчета относительной погрешности результата косвенных измерений объема шарика. Здесь удобнее воспользоваться методом :

, , , т.к. ,

( рассматриваем как переменную, так как его можно брать с различным числом десятичных знаков). , так как имеет множество значений. Переходя к приращениям, получим:

, .

Следовательно, число после округления надо взять с точностью до 4-го знака после запятой, т.е. , так как , что приблизительно на порядок . Тогда окончательно получим:

,

где . Следовательно, .

Результат запишем в виде .

3. Правила построения графиков экспериментальных зависимостей

При построении графиков к лабораторным работам обычно используют прямоугольную систему координат, а поле графика выбирают размером приблизительно в страницу тетради. Желательно использовать миллиметровую бумагу.

Для правильного построения графика необходимо выполнить следующие операции: задать масштабы по вертикальной и горизонтальной осям. Масштабы должны быть такими, чтобы рационально использовать всю площадь чертежа. Координатные оси отмечают буквами, обозначающими фиксируемые физические величины, указывают их размерность.

Полученные экспериментальные данные наносятся на график в виде крестиков, кружочков и т.д. Нанесенные экспериментальные точки не следует соединять отрезками прямых. Необходимо провести гладкие кривые, соответствующие изучаемым физическим зависимостям. Из-за наличия погрешностей экспериментальные точки, как правило, не лежат на усредняющей кривой. При правильно проведенной кривой экспериментальные точки равномерно отклоняются от неё, показывая относительную случайную погрешность по оси абсцисс.

В верхней части прямоугольной системы координат необходимо указать приведенную на графике зависимость.

Пример. Построить градуировочную кривую ультрафиолетового монохроматора - зависимости длины волны от показаний отсчетного барабана .

При построении градуировочного графика для монохроматора, работающего в ультрафиолетовой области, длины волн исследуемого диапазона лежат в интервале от 248,3 нм до 389,9 мм. Следовательно, нет смысла по оси ординат брать начало координат при . Разумно за начало принять .

Примечание. Обычно по оси ординат откладывают искомую величину функцию, а по оси абсцисс - аргумент. В нашем примере по оси абсцисс должны быть деления отсчетного барабана монохроматора, а по оси ординат .

Подобрать масштабы по осям абсцисс и ординат таким образом, чтобы:

а) занять почти все поле построения графика;

б) в него попали и наибольшее и наименьшее значения величин, по которым строят график. При этом масштабы следует выбирать таким образом, чтобы деления миллиметровой линейки (1 мм, 5 мм, 10 мм) соответствовали 1-ой, 5-ти, 10-ти… единицам откладываемой по осям величины (или их доле:10^-1,10^-2 ...).

Проставить на осях числа, отвечающие выбранным масштабам, а у стрелок осей записать символы откладываемых величин и их масштабы, например, мкм или нм.

Нанести на бумагу экспериментальные точки и вокруг них нарисовать кружочки (○) или треугольники (▲) или обозначить их крестиками, причем таким образом, чтобы их размеры приблизительно соответствовали погрешностям.

По нанесенным точкам провести плавную (но не зигзагообразную!) кривую таким образом, чтобы число экспериментальных точек по обе стороны от проводимой кривой было, приблизительно одинаковым.

Таблица результатов

№ точки	Длина волны, нм	Показания отсчетного барабана	N ср.
N	N	N	N
	248.3	236.2	236.0	235.8	236.0	0.13
	265.2	250.5	250.1	250.0	250.2	0.2
	275.3	258.0	258.0	258.3	258.1	0.1
	280.4	261.8	261.0	261.1	261.3	0.3
	296.7	274.3	274.3	274.3	274.3	0.0
	312.6	285.3	285.8	285.8	285.7	0.25
	334.1	301.3	301.0	301.6	301.3	0.2
	365.0	322.1	322.0	322.5	322.2	0.2
	388.9	337.2	337.5	337.5	377.4	0.13

Начало координат по оси ординат берем при , а по оси абсцисс - при .

По граничным значениям табличных данных выбираем масштабы:

а) по оси ординат ,

б) по оси абсцисс ,

Проставляем по осям соответствующие числа и обозначения:

и – с указанием масштабов.

Наносим экспериментальные точки и проводим по ним плавную кривую. Радиус кружочков определяется и в нашем случае это практически точки. Поэтому вместо кружочков мы используем крестики.

В результате этих операций получаем градуировочный график УФ монохроматора.

На приведенном рисунке видно, что точка А лежит вдали от плавной градуировочной кривой. Это грубая погрешность: вместо записано (по ошибке!) . Поэтому эту точку надо перепроверить и нанести (на поле графика) заново или исключить. Из приведенного примера ясно, что график надо строить сразу после выполнения лабораторной работы, в лаборатории.

Мы рассмотрели такой случай, когда вид кривой неизвестен. Однако в ряде случаев заранее ясно, что график должен быть прямой или может быть приведен к прямой за счет откладывания по осям не самих величин, а их функций, либо благодаря специально выбранной методике обработки результатов наблюдений.

Примеры.

1) В случаях градуировки баллистического гальванометра, веберметра, конденсатора переменной емкости, термопары и работы с пирометром заранее известно, что должна получиться прямая.

2) При изучении равноускоренного движения

мы можем получить линейную зависимость, если представить его в виде:

.

3) При проверке закона Малюса мы имеем две закономерности - теоретическую и экспериментальную , причем должна быть близка к . Таким образом, проверку закона Малюса можно свести к построению кривой, близкой к прямой, если ввести функцию .

Следовательно, чем ближе к прямой, тем точнее выполняется закон Малюса.

В итоге желательно делать так, чтобы ожидаемые кривые, если возможно, были заменены прямыми, так как это существенно упрощает построение графиков и проверку изучаемых закономерностей.

Примечание. Часто для точного построения графика используют метод наименьших квадратов.

Вопросы для защиты в форме круглого стола

По II разделу

№ пп	Вопросы	Рекомендов. Литература
№.	Стр.
	Примеры колебательных процессов в живом организме; гармонические колебания, их уравнение и характеристики колебания.		219-221
	Вывод формулы для частоты свободных колебаний пружинного маятника на основе его уравнения движения.
	Маятники: пружинный, математический, физический. Формулы для периода и частоты их колебаний.		222-223
	Свободные затухающие колебания, зависимость их амплитуды от времени; характеристики затухания.		139-140 229-231
	Кинетическая и потенциальная энергия при механических колебаниях.
	Вынужденные колебания. Резонанс. Связь резонансной частоты и коэффициента затухания системы. Возможный вред резонанса для организма.		141-143
	Механические волны в средах; продольные и поперечные волны. Энергии, переносимая упругой волной, вектор Умова.		145-146
	Уравнение плоской волны, её характеристики.
	Звук как упругая волна. Скорость звука в твердых телах, жидкостях и газах.		37-39
	Звук как физиологическое явление; звуковое давление, физика слуха.		160-164 52-58
	Единицы измерения интенсивности звука, шумовые характеристики и нормы.		52-57 153-156
	Эффект Доплера в акустике.		49-52 148-150
	Звукоизлучение и звуковосприятие в животном мире.		58-60
	Биофизика инфразвука.		68-71
	Получение и регистрация ультразвука. Ультразвук в мире животных.		72-74, 79-80
	Взаимодействие ультразвука с веществом.		74-77
	Ультразвуковая диагностика.		82-88
	Применение ультразвука в ветеринарии: УЗ терапия и УЗ хирургия.		80-82 164-167