Временные параметры сетевого графика

Каждой дуге сетевого графика поставим в соответствие некоторое число, соответствующее продолжительности работы, отображаемой данной дугой. Число, приписанное дуге (i,j), будем называть длиной дуги и обозначать t_ij.

Множество дуг, упорядоченное таким образом, что конечное событие одной из них является начальным событием другой, называется путем.

Рассмотрим небольшой пример.

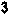
Рис. 4

Будем различать четыре вида пути:

а). Полный путь – путь, начало которого совпадает с исходным событием сети, конец – с завершающим, например, (0,1)-(1,4)-(4,5)-(5,6) или (0,2)-(2,4)-(4,6).

б). Путь, предшествующий событию – это путь от исходного события до данного события, например, для события 4 предшествующими путями будут (0,2)-(2,4) и (0,1)-(1,4).

в). Путь, следующий за событием – это путь от данного события до завершающего, например, для события 2 это пути (2,4)-(4,5)-(5,6) и (2,4)-(4,6).

г). Путь между двумя событиями – путь, начало и конец которого совпадают с соответствующими событиями, например, между событиями 2 и 5 лежит путь (2,4)-(4,5).

Под длиной пути будем понимать продолжительность выполнения всей последовательности работ, составляющих данный путь.

Таким образом, длина пути равна сумме длин всех дуг данного пути.

Наиболее продолжительный полный путь в сетевом графике называется критическим. Критическими называются также работы и события, расположенные на этом пути.

Рассмотрим еще один пример сетевого графика. Цифры на каждой дуге означают продолжительности работ.

4 3 3

2 3

6 4 5

5 1 8

2 10 Рис. 5

Здесь полными путями будут:

путь (0,1)-(1,3)-(3,6)-(6,8) продолжительностью 2+4+3+3=12,

путь (0,3)-(3,6)-(6,8) продолжительностью 3+3+3=9,

путь (0,2)-(2,3)-(3,6)-(6,8) продолжительностью 5+6+3+3=17,

путь (0,2)-(2,5)-(5,7)-(7,8) продолжительностью 5+1+8+5=19,

путь (0,2)-(2,5)-(5,8) продолжительностью 5+1+4=10 и

путь (0,2)-(2,4)-(4,7)-(7,8) продолжительностью 5+2+10+5=22.

Перебрав все полные пути, мы видим, что последний путь имеет наибольшую продолжительность, поэтому он и является критическим (далее мы приведем способ определения критического пути без перебора всех полных путей). Продолжительность критического пути составляет 22 (например, дня), т.е. для проведения всего комплекса работ понадобится 22 дня. Быстрее комплекс выполнить нельзя, так как для достижения цели (завершающего события) работы критического пути надо выполнить обязательно. Определив критический путь, мы тем самым установили критические события сети 0,2,4,7,8 и критические работы (0,2), (2,4), (4,7), (7,8).

Критический путь имеет особое значение в системах сетевого планирования и управления. Действительно, срыв сроков выполнения какой-либо работы критического пути влечет срыв срока выполнения всего комплекса в целом, и, с другой стороны, для сокращения продолжительности проекта необходимо в первую очередь сокращать продолжительность работ, лежащих на критическом пути.