Эффективные параметры неоднородности среды

Понятие однородности или неоднородности среды тесным образом связано с понятием симметрии. Мы называем однородной средой ту, у которой свойства не меняются при координатных преобразованиях от точки к точке, произошедших, либо за счет движений - трансляций, либо за счет поворотов. Следовательно, однородность среды - это ее симметрия при координатных преобразованиях. Наоборот, нарушение этой симметрии, состоящее в том, что при сдвиге или повороте свойства в новой точке иные - т.е. несимметричность среды относительно такого рода преобразований, ассоциируется с неоднородностями, присущими среде. Однако если факт однородности среды достаточно ясно и очевидно связан с ее симметрией при координатных преобразованиях, то нарушение симметрии как свойство неоднородности и, соответственно, неоднородность как проявление нарушения симметрии, очевидным и привычным образом не выражаются друг через друга.

Пусть задана группа Ли линейных координатных преобразований g(s), некоторый произвольный элемент которой будем обозначать символом R1. 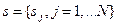- - 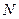мерный параметр. Например, его размерность может совпадать с размерностью пространства. Пусть далее G(s) - представление группы g(s) на пространстве полей. Произвольный элемент этой группы, соответствующий элементу R, будем обозначать В. Вариация лагранжиана, вызванная преобразованиями координат и полей операторами R и В, равна:

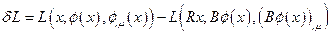(4.10)

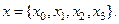
Если лагранжева плотность не зависит явно от пространственно-временных координат, то в вариации (10) участвует только оператор В. Если эта вариация обращается в ноль, то операторы R и В, являясь операторами из группы симметрии, порождают уже описанным в предыдущем разделе образом уравнения поля в среде - уравнения Эйлера и законы сохранения.

Определение. Среда называется однороднойдля заданного поля, относительно группы преобразований 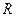, если вариация лагранжевой плотности при преобразованиях из 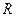и их представлениях на физических полях, имеют вид (10) и .

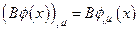Строго говоря, под такое определение попадают и среды, которые в привычном смысле являются неоднородными. Это оправдано тем, что в дальнейшем мы намерены изучать и описывать с помощью понятия нарушения симметрии неоднородности «сверх заданных», «сверх уже входящих» в уравнения, и лагранжеву плотность для поля.

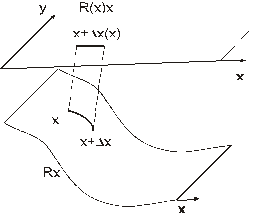Неоднородность среды можно ассоциировать с зависимостью преобразования R из группы g(s) от координат так, что результат применения оператора R к неоднородной среде зависит от пространственно–временных координат точки приложения этого оператора. Например, сдвигая глобально систему координат, получим локальное изменение координат, величина которого зависит от координат рассматриваемой точки. Ситуация аналогична тому, как если бы глобально сдвигалась некоторая «кривая» поверхность, а значения новых координат рассматривались в проекции ее на плоскость (Рис.Пр.4.1). Неоднородность средыпредставляется в виде кривизны координатной системы.

Зависимость от координат оператора R влечет за собой зависимость от координат B из G(s), реализующих представление группы g(s) на пространстве физических полей. Эта зависимость (операторов R и В от координат) называется локальным нарушением симметрии.

В пространствах с локально нарушенной симметрией трансформационные свойства поля, при преобразованиях координат операторами R и поля оператором В такие же, как и в пространствах с ненарушенной симметрией. Это означает, что закон их преобразования одинаков, как при зависящих, так и при не зависящих, от координат операторов R и В.

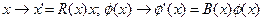. (4.11)

Однако этот закон нарушается для производных поля[47]. В то время как в пространстве с ненарушенной локальной симметрией, производная поля трансформируется по закону: 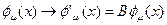, в пространствах с локально нарушенной симметрией имеем:

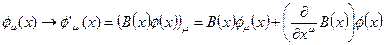. (4.12)

Дополнительно появившийся в законе трансформации производных поля при локальном нарушении симметрии, член:

,

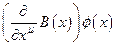приводит к тому, что в пространствах с локально нарушенной симметрией меняется и закон (10) трансформации лагранжиана:

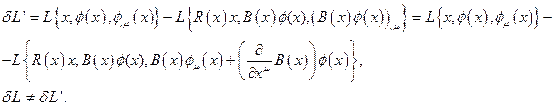
Рассмотрим случай возможных не коммутирующих операторов В и вычисления производной для пространств с ненарушенной симметрией. В пространствах с локально ненарушенной симметрией координатные преобразования 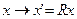влекут за собой преобразования поля по закону 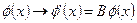, а это, в свою очередь, влечет закон трансформации для производной по правилу: .

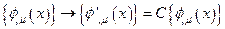Здесь 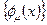строка производных, которая взята в скобки для того, чтобы подчеркнуть, что набор производных образует единый объект. Локальное нарушение симметрии производит к тому, что преобразование поля 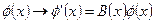влечет преобразование производныхпо правилу

.

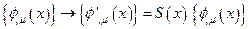За счет возможного отличия оператора S от оператора С и происходит нарушение трансформационных свойств производных. Однако столь общая постановка вне конкретизации вида операторов С приводит к громоздким и мало что дающим рассмотрениям. Поэтому в настоящем разделе мы рассмотрим случай теории коммутирующих операторов дифференцирования и В в пространствах с ненарушенной симметрией. Описанный выше случай самостоятельного закона преобразования для производных рассмотрим в следующем разделе на конкретном содержательном примере пространств с афинной связностью.

Неоднородности среды ассоциируются, как уже указывалось ранее, с локальным нарушением симметрии, а последнее можно образно представить как искривление пространственно-временной сцены, на которой происходит соответствующий физический процесс. Характер этого искривления и есть проявляющиеся в регистрируемом физическом поле неоднородности среды. Для неоднородной среды в таком понимании неоднородностей, законы преобразования энергетических характеристик, системы: среда-поле должны быть теми же самыми, что и в однородном случае, но действуют в искривленном многообразии – пространстве-времени. Таким образом, следует обеспечить совпадение трансформационных свойств лагранжевой плотности, как в пространствах с локально нарушенной, так и ненарушенной симметрией. Так как именно она является энергетической характеристикой системы, будучи разностью, между плотностью кинетической и потенциальной энергией.

Поскольку отличие в трансформационных свойствах лагранжевой плотности возникает за счет производных поля, то именно это понятие должно быть переопределено так, чтобы обеспечить совпадение трансформационных свойств лагранжиана в пространствах с локально нарушенной и ненарушенной симметриями. Необходимость переопределения производных и подчеркивает факт интерпретации локального нарушения симметрии как изменения геометрической характеристики пространственно-временной сцены. Действительно, на способ определения производных, а через них уже и на все иные аналитические объекты, влияют, прежде всего, геометрические характеристики многообразия.

В качестве нового, обобщающего старое, определения производной поля примем:

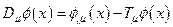(4.13)

Здесь 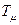- линейные операторы, действующие на поле 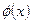, которые далее будем называть объектами связности. Эти операторы предназначены для компенсации членов 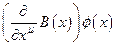, присутствующих в законе трансформации для производных поля в пространствах с нарушенной симметрией. Следовательно, их вид должен быть аналогичен виду операторов .

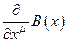Оператор В является одним из операторов группы Ли G(s) и, следовательно, при некотором значении параметра s B=G(s). Зависимость оператора В от координат означает, по существу, зависимость от координат значения параметра s, при котором В(х)=G(s(x)). Следовательно:

.

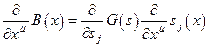Будем считать, что операторнозначная функция G(s) регулярная в области значений параметра s. Это означает, что пространства векторов (называемых касательными), составленные из линейных комбинаций элементов:

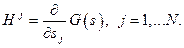
совпадают между собой для всех s из рассматриваемой области значений этого параметра. Тогда операторы 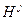могут быть представлены как линейные комбинации генераторов 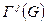, j=1,…N группы G(s). Таким образом, 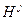- элементы алгебры Ли AG группы G. Следовательно, для операторов

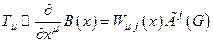, (4.14)

где: 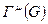- генератор группы 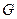2, образующие алгебру Ли AG этой группы; 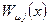- для каждого индекса j векторное поле 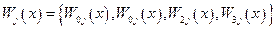, которое называется калибровочным полем симметрии, соответствующей генератору 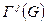. Число таких векторных полей равно числу генераторов группы G. Таким образом, каждому генератору группы симметрий, которая предполагается нарушенная, ставится в соответствие калибровочное поле, которое и служит количественным выражением нарушения симметрии. Функции 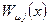следует рассматривать как зависящие от координат коэффициенты, определяющие новую производную:

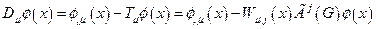. (4.15)

Так определенную производную называется удлиненной. Удлиненная производнаявводится для того, чтобы обеспечить выполнение в пространствах с локально нарушенной симметрией закона трансформации для удлиненной производной, аналогичного закону трансформации обычной производной в однородном пространстве-времени. Именно, если: 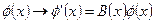, то должно быть выполнено правило:

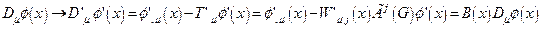. (4.16)

Замена в лагранжевой плотности обычных производных удлиненными приводит к тому, что все компоненты лагранжевой плотности в пространствах с нарушенной и ненарушенной симметрией преобразуются одинаково. В последнем случае лишь функции 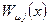обращаются в ноль, что свидетельствует об однородности среды.

Правило трансформации (16) будет выполнено, если при преобразованиях (11) объекты связности 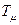преобразуются по закону:

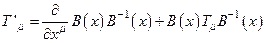. (4.17)

Действительно, из (16) следует:

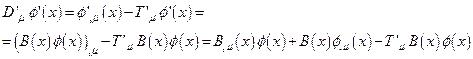
C другой стороны:

,

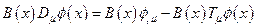тогда из требования

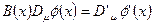получаем: .

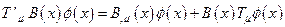Применяя к последнему соотношению справа, оператор 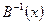, получим искомый закон преобразования (17) объектов связности при преобразованиях поля по закону (11).

При определении удлиненной производной (15) можно пользоваться и положительным вторым слагаемым:

.

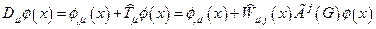Операторы 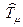- это так же объекты связности, выполняющие роль компенсации членов 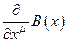. Однако это другие объекты связности, отличающиеся от 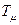и имеющие несколько отличный от (17) закон преобразования. Этот закон легко находится приемом уже описанным выше: 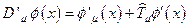. Действительно,

.

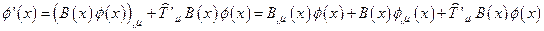Далее:

,

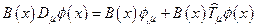тогда из требования:

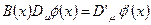, следует:

.

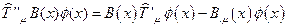Из последнего соотношения следует искомый закон преобразования

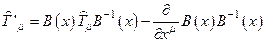. (4.17-1)

Преобразования (17) называются калибровочными, и их смысл состоит в том, что они дают закон преобразования для объектов связанности 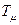, характеризующих неоднородности среды через зависящий от пространственно-временных координат результат действия того, либо иного, преобразования симметрии из G(s). Если объекты связанности могут быть представлены в виде:

,

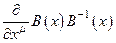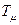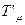то они называются чисто калибровочными. Объекты связанности и , связанные между собой отношением (17), называются калибровочно-эквивалентными. Таким образом, все множество объектов связности разбивается на множество не пересекающихся классов калибровочно-эквивалентных объектов связанности. Часть из них – чисто калибровочные, содержат нулевой член и, следовательно, надлежащим координатным преобразованием все они могут быть сведены к нулю.

Формула (17) преобразования объектов связанности еще раз подтверждает правильность их представления в виде (14), так как из (17) следует, что 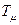принадлежат области значений выражения

.

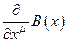Выберем в четырехмерном пространстве замкнутый прямоугольный контур со сторонами: 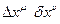. Подсчитаем разность приращений поля, полученных при движении

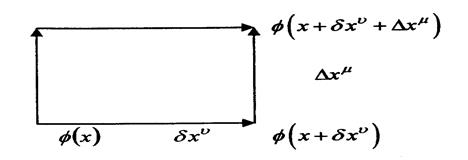
Из одной точки в другую по двум разным направлениям, показанныи на рис. Пр.4.2 стрелками. Получим:

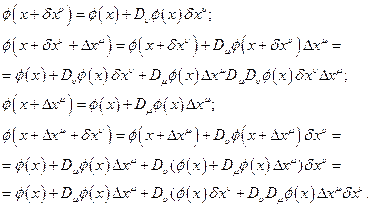
Следовательно, разность приращений поля 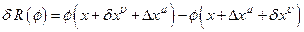равна:

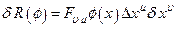, (4.18)

где:

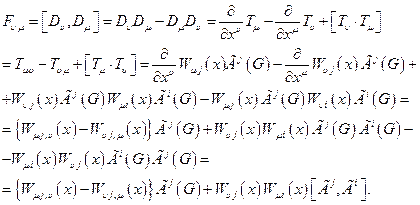(4.19)

Величину 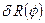естественно назвать кривизной, а оператор - операторы кривизны.В связи с тем, что оператор кривизны представляет собой антикоммутатор удлиненных производных, его трансформационные свойства те же, что и удлиненной производной. Т.е. при преобразовании 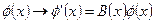имеем:

.

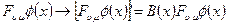С другой стороны,

.

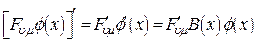Следовательно:

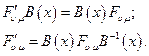(4.20)

Из последнего соотношения, в частности, вытекает, что если объект связанности калибровочно-эквивалентен нулю, то его оператор кривизны тождественно равен нулю. Действительно, для нулевого объекта связанности кривизна равна нулю. Это следует из (18). Любой другой ему калибровочно-эквивалентный получается по (20), что так же всегда дает ноль.

Для того чтобы построить уравнения, описывающие поведение поля в пространствах с локально нарушенной симметрией, следует в лагранжевой плотности 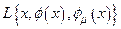заменить обычные производные 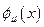удлиненными 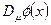. Далее, варьируя, таким образом, полученное новое действие:

,

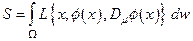в предположении его экстремума получаем, в соответствии с принципом наименьшего действия, уравнения Эйлера, которые и являются уравнениями поля в пространствах с локально нарушенной симметрией. Неоднородности среды характеризуются калибровочными полями

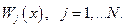
Таким образом, последовательность получения обобщения уравнений, описывающих физический процесс в пространствах с локально нарушенной симметрией, выглядит следующим образом: для исходного уравнения выписывается лагранжева плотность; выбирается группа Ли симметрий, локальное нарушение которой принимается за описываемую неоднородность; находятся представления этой группы на функциях поля и ее генераторы – базисные элементы соответствующей алгебры Ли. Далее в лагранжевой плотности производные заменяются их удлиненными аналогами с использованием калибровочных полей, после чего варьированием этой новой лагранжевой плотности получают уравнение Эйлера как уравнение поля в пространствах с локально нарушенной симметрией.

Если поле 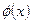М – компонентно, т.е. 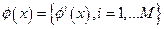, то система уравнений поля в среде с локально нарушенной симметриейимеет вид:

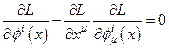, (21)

где 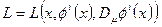. При этом поле 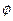в однородной среде имеет лагранжиан .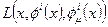