I. Применение модели наращения
1. Модель начисления простых процентов. Особенности начисления: 1). Обычно используются в краткосрочных финансовых операциях, срок не более 1 года; 2). База начисления процентов не меняется и равна первоначальной сумме.
Обозначим годовую ставку начисления простых процентов  . Проценты, или интерес за t лет составят
. Проценты, или интерес за t лет составят  . А наращенная сумма будет равна
. А наращенная сумма будет равна  . Если же длительность краткосрочной операции определяется в днях, а не в относительных долях от года, то необходимо вычислить какая доля процентов придется на этот срок, т.е.
. Если же длительность краткосрочной операции определяется в днях, а не в относительных долях от года, то необходимо вычислить какая доля процентов придется на этот срок, т.е.  , где
, где  - количество дней в году (временная база).
- количество дней в году (временная база).
Существует три способа определения срока:
1. «английская практика» или точные проценты с точным числом дней. Используется в Великобритании, США, Португалии. Количество дней ссуды определяется точно по календарю. В году 365 дней  .
.
2. «французская практика» или обыкновенные проценты с точным числом дней. Количество дней рассчитывается точно по календарю, а число дней в году 360. Используется во Франции, Бельгии, Испании.
3. «германская практика» или обыкновенные проценты с приближенным числом дней. Используется в Германии, России, США. Количество дней в каждом месяце одинаково и равно 30, число дней в году 360. Применяется для промежуточных расчетов. Следует отметить, что в расчетах первый и последний день принимается за один.
Пример.
Выдан кредит на сумму 3 млн. руб. с 16.01.11 по 16.03.11 под 12% годовых. Найти сумму погасительного платежа.
Решение.
Срок кредита меньше года, поэтому для расчета погасительного платежа используем простые проценты. Найдем его величину тремя способами.
1. «английская практика».
Срок операции в днях вычисляем точно. В январе число дней, входящих в срок кредита составляет 31-15=16 дней, в феврале – 28 дней, в марте – 16 дней. Итак срок операции t будет равен t=16+28+16-1=59 дней. Срок уменьшается на 1 день за счет того, что первый и последний день принимается за один. По английской практике число дней в году  дней.
дней.
Вычислим сумму погасительного платежа по модели простых процентов:  . Здесь
. Здесь  млн руб. t=59 дней. Тогда:
млн руб. t=59 дней. Тогда:  руб.
руб.
Должник заплатит сумму процентов 58191,78 руб.
2. «Французская практика».
Количество дней кредита остается таким же, как в английской практике, потому что вычисляется точно по календарю. Изменяется только временная база 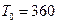 дней. Вычислим величину погасительного платежа:
дней. Вычислим величину погасительного платежа:
 руб.
руб.
Если сумма погасительного платежа вычисляется по этой практике, то сумма, которую заплатит должник будет больше, чем при использовании английской. Она составит 59000 рублей.
3. «Германская практика».
Количество дней кредита изменяется, потому что в каждом месяце количество дней равно 30. Тогда в январе число дней финансовой операции будет 30-15 дней, в феврале 30 дней, в марте – 16 дней. Вычислим срок кредита t=15+30+16-1=60 дней. Временная база 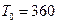 дней. Найдем величину погасительного платежа:
дней. Найдем величину погасительного платежа:  рублей.
рублей.
Погасительный платеж по этому способу оказался самым высоким. Сумма процентов, заплаченная по кредиту, равна 60000 рублей.
2. Модель начисления сложных процентов.
Модель обычно используется, когда срок финансовой операции охватывает целое число лет t. Основное отличие сложных процентов от простых: изменяется база начисления процентов при переходе от одного расчетного периода к следующему; к основной сумме прибавляются процентные деньги за расчетный период и эта новая сумма становится базовой для начисления процентов на следующий период. Происходит начисление «процента на процент» или капитализация процентов. Наращенная величина денежной суммы под конец расчетного вычисляется по формуле  , где t – количество лет,
, где t – количество лет, 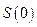 - начальная денежная величина,
- начальная денежная величина, 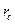 - ставка сложных процентов. На практике бывает так, что требуется начислить сложные проценты на нецелое число лет, тогда показатель степени будет дробным.
- ставка сложных процентов. На практике бывает так, что требуется начислить сложные проценты на нецелое число лет, тогда показатель степени будет дробным.
Пример. Вклад в размере 40000 руб внесен в банк по 25% годовых. Сколько получит клиент через а) 2 года; б) 6 месяцев? Начисляются сложные проценты.
Решение.
А). срок финансовой операции является целым числом t =2 года. Согласно условию задачи  руб,
руб, 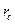 =0,25. Тогда
=0,25. Тогда 
Б). срок операции дробный, поэтому  , так как 6 месяцев составляет
, так как 6 месяцев составляет  или
или  года. Применим схему сложных процентов, как требуется в задаче:
года. Применим схему сложных процентов, как требуется в задаче:  руб. вычислим, какая сумма будет выплачена клиенту банком, если на этот срок будут начислены простые проценты:
руб. вычислим, какая сумма будет выплачена клиенту банком, если на этот срок будут начислены простые проценты:  , здесь t – время в относительных долях года. Тогда
, здесь t – время в относительных долях года. Тогда  рублей. Сравним полученные результаты. На срок, меньший года, по модели простых процентов величина начисленных процентов выше, чем по модели сложных.
рублей. Сравним полученные результаты. На срок, меньший года, по модели простых процентов величина начисленных процентов выше, чем по модели сложных.
в). На практике, когда срок платежа превышает 1 год, и его величина состоит из нецелого количества периодов, то применяют модель комбинированного начисления процентов.
Сложные проценты будут начислен за целое число лет (периодов) t, а простые проценты на оставшуюся дробную:  , где
, где  - целая часть срока,
- целая часть срока,  - дробная часть срока, выраженная в долях года,
- дробная часть срока, выраженная в долях года,  - процентная ставка наращения. Если же дробная часть срока дана в днях, то
- процентная ставка наращения. Если же дробная часть срока дана в днях, то  .
.
Пример.
Срок финансовой операции 2,5 года. Клиент вложил 40000 рублей в банк по 25 %. Определить, какая сумма будет выплачена банку? Использовать модель сложных процентов и модель комбинированных. Сравнить результаты.
Решение.
1. Начислим проценты по комбинированной схеме.
Согласно условию задачи  руб, целая часть срока
руб, целая часть срока  = 2 года, дробная часть
= 2 года, дробная часть  =0,5,
=0,5,  =0,25. Тогда:
=0,25. Тогда:  рублей.
рублей.
2. Проведем начисление по сложным процентам:  руб.
руб.
Итак, начисление по схеме комбинированных процентов дает большую наращенную величину первоначального вклада, чем начисление только по сложным процентам. Можно убедиться, что начисление простых процентов на этот срок даст еще меньшую величину наращенной суммы:  руб.
руб.
