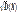Равномерное распределение. Показательное распределение. Вероятность попадания СВ в заданный интервал

1. равномерный закон распределения.З-н распределения непрерывной случайной величины Х, принимающей все свои значения из отрезка [a,b] называется равномернымесли ее плотность распределения р(х) на этом отрезке постоянна, а вне его равна 0. Т.е.
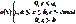Используя св-ва плотности распределения можно найти постоянную С. С= .

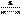Используя формулу F(x)= 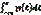можно найти ф-ию распределения: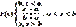

С равномерным распределением встречаются всякий раз, когда условия опыта величина Х принимает значение в конечном промежутке [α;β]. Все значения из этого промежутка возможны в одинаковой степени, причем ни одно из значений не имеет преимуществ перед одним.

М(Х)= 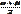-мат. ожидание для случайной величины Х, распределенной по равномерному з-ну.

D(X)= 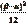- дисперсия случайной величины Х, имеющей равномерный з-н распределения.

δ(X)= 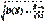- среднее квадратическое отклонение Х, им. равномерный з-н распределения. 2.Показательное распределение –распределение с плотностью вероятностей, имеющей след. вид:
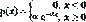Ф-ия распределения F(X) случайной величины Х, распределенной по показательному з-ну имеет следующий вид:
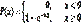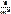Показательный з-н распределения вероятностей встречается во многих задачах, связанных с простейшим потоком событий. Под потоком событийпонимают последовательность событий наступающих одно за другим в определенные моменты (случайные моменты). М(Х)= - мат. ожидание случ. величины Х, им. показательный з-н распределения D(X)= - дисперсия случайной величины Х, им. показательный з-н распределения δ(X)= 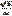Теорема:вероятность попадания непрерывной случайной величины Х в интервал (а,в) равна определенному интегралу от ее плотности распределения р(х) по отрезку [a, b], т.е. Р(а<X<b)=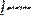

Осн. хар-ки генеральной и выборочной сов-ти.

* пусть требуется изучить дискретную генеральную сов-ть относительно колич. признака Х. Пусть распределение колич. признака Х генеральной сов-ти известно и задано таблицей:

варианты	х1	х2	…	хк
частоты	N1	N2	…	Nk

N₁+N₂+…+N_k=N Ср. арифмет. (мат. ожидание) распределение признака Х ген. сов-ти вычисляется по ф-ле:

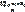= - генеральная средняя.

D₀(X)= 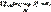- дисперсия.

Предположим, что для изучения генеральной сов-ти относительно колич. признака Х из нее извлечена выборка объема n. *распределение признака Х в выборочной сов-ти будем считать также известным и предст. в виде таблицы:

варианты	х1	х2	…	хк
частоты	n1	n2	…	nk

n₁+n₂+…+n_k=n

Ср. арифмет. (мат. ожидание) и дисперсия распределения признака Х в выборочной сов-ти назыв. выборочной средней и выборочной дисперсией соотв. Они находятся по соотв. формулам:

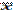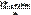= D(X)=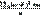

Средние квадрат. отклонения: δ₀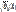₌ ; δ₌