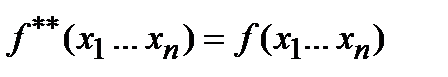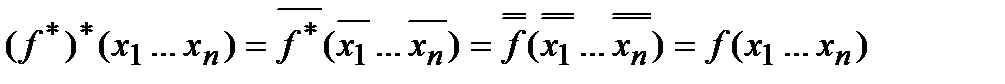Представление функции в виде совершенной дизъюнктивной и совершенной конъюнктивной формах. Разложение функции по начальному множеству переменных
Теорема о представлении любой булевой функции в виде СДНФ: для любой булевой функции справедлива следующая формула :
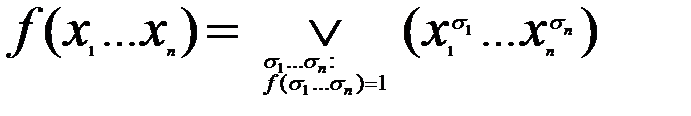
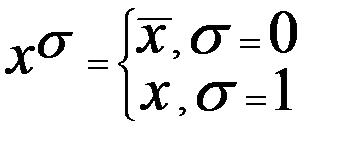
| x1 | x2 | x3 | f | |
| 0 | 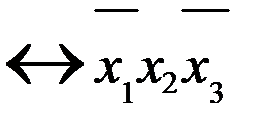 | |||
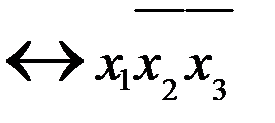 | ||||
| 1 | 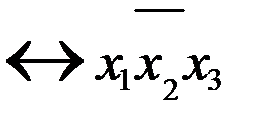 | |||
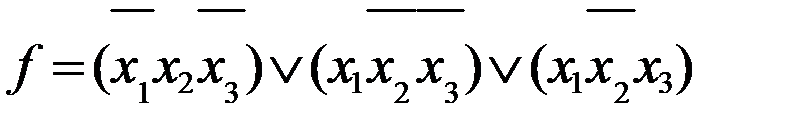
Доказательство:
Свойства 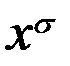
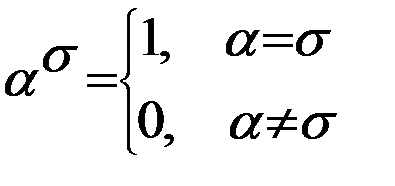
1)
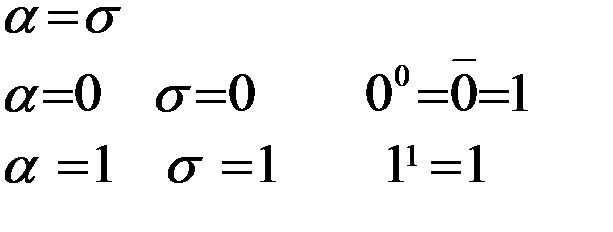
2)
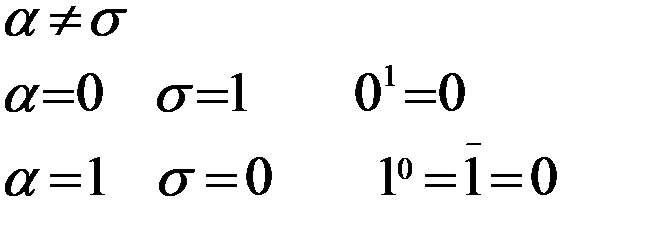
Чтобы доказать теорему покажем выполнение данного равенства на любом двоичном наборе ,то есть что левые и правые части совпадают для любого двоиного набора:
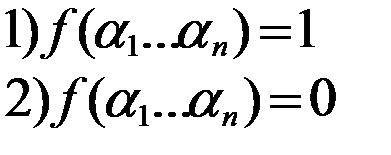 .
.
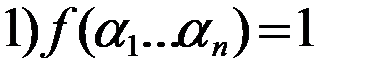 . То есть левая часть равенства равна 1. Покажем,что и правая часть равенства также равна 1 на данном наборе. Для этого достаточно показать,что хотя бы одно слагаемое правой части равно 1.
. То есть левая часть равенства равна 1. Покажем,что и правая часть равенства также равна 1 на данном наборе. Для этого достаточно показать,что хотя бы одно слагаемое правой части равно 1.
Таким слагаемым будет слагаемое, которое соответствует единичному набору s, совпадающего с набором a.
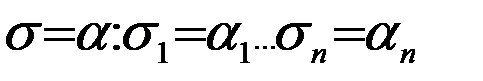 .
.
Значение этого слагаемого на наборе 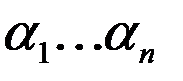 есть
есть
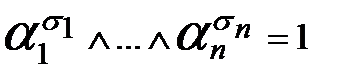 в силу того ,что значение каждого множителя равно 1. Последнее справедливо в силу свойства символа
в силу того ,что значение каждого множителя равно 1. Последнее справедливо в силу свойства символа 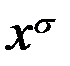 .
.
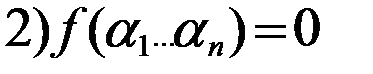 . То есть левая часть равна 0. Покажем, что и правая часть также равна 0. Для этого нужно показать, что значение всех слагаемых равно 0. Рассмотрим произвольное слагаемое правой части, которое соответствует некоторому двоичному набору
. То есть левая часть равна 0. Покажем, что и правая часть также равна 0. Для этого нужно показать, что значение всех слагаемых равно 0. Рассмотрим произвольное слагаемое правой части, которое соответствует некоторому двоичному набору 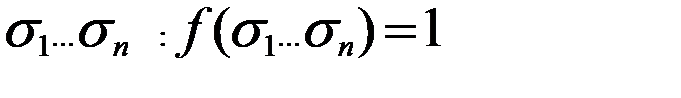 , тогда
, тогда 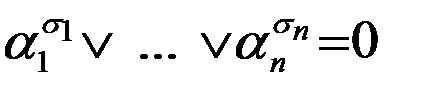 в силу, того, что наборы a и s различны, т.к. a - набор, на котором значение функции равно 0, а s - набор, на котором значение функции равно 1. Так как наборы различны, то существует множитель i:
в силу, того, что наборы a и s различны, т.к. a - набор, на котором значение функции равно 0, а s - набор, на котором значение функции равно 1. Так как наборы различны, то существует множитель i: 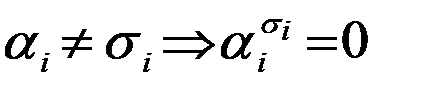 , а поэтому и все произведение равно 0.Таким образом каждое слагаемое равно 0, следовательно и вся сумма равна 0, значит правая часть равна 0.
, а поэтому и все произведение равно 0.Таким образом каждое слагаемое равно 0, следовательно и вся сумма равна 0, значит правая часть равна 0.
Теорема полностью доказана.
| x1 | x2 | x3 | f | 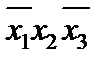 | 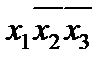 | 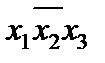 | 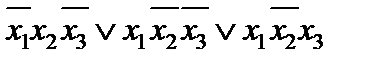 |
Теорема о разложении булевой функции по первым k-переменным.
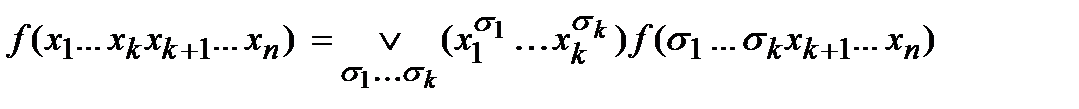
Доказательство:
Рассмотрим произвольный набор значений переменных 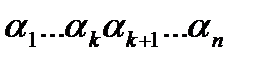 , и покажем, что левая и правая часть равны. Левая часть -
, и покажем, что левая и правая часть равны. Левая часть - 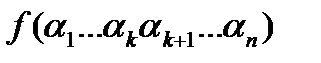 .
.
В правой части рассмотрим слагаемое, в котором значение набора s совпадает с первыми k-компонентами набора a: 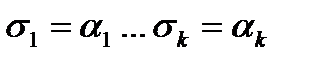 .
.
Значение этого слагаемого на наборе 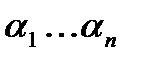 равно
равно 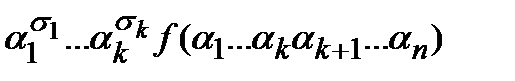 .
.
В силу того, что набор s и первые k-компонент набора a совпадают, рассматриваемые множители равны 1, все слагаемое равно 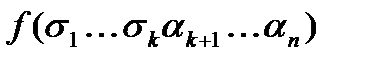 . Все остальные слагаемые равны 0 в силу того, что среди множителей
. Все остальные слагаемые равны 0 в силу того, что среди множителей 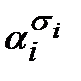 обязательно найдется множитель, в котором a и s различаются, а это нулевой множитель. Поэтому правая часть равна
обязательно найдется множитель, в котором a и s различаются, а это нулевой множитель. Поэтому правая часть равна 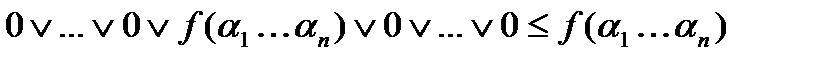 (все слагаемые, кроме быть может одного, равны 0).
(все слагаемые, кроме быть может одного, равны 0).
Теорема доказана.
Нетрудно убедиться в справедливости следующих тождеств:
1) 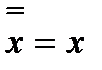 6)
6) 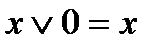
2) 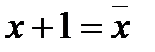 7)
7) 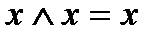
3) 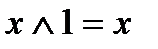 8)
8) 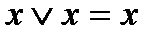
4) 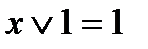 9)
9) 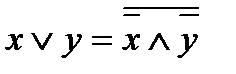
5) 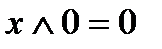 10)
10) 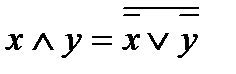
Доказательство предлагается в качестве домашних упражнений.
Последние два тождества называются правилами Де-Моргана.
Определение.
Двойственной к функции 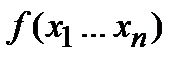 называют функцию
называют функцию 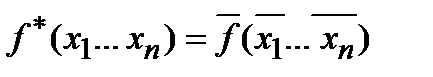 .
.
Например, двойственной к конъюнкции является
дизъюнкция, и наоборот, двойственной к дизъюнкции является конъюнкция.
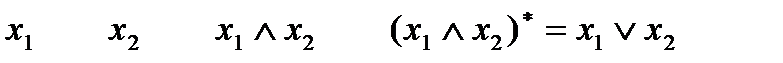
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 1
Утверждение. Двойственной к двойственной функции есть сама функция, т.е.