Приближения для дробных возрастов

Округленное время жизни 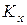определили через точное время жизни 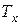и получили ряд формул, выражающих характеристики величины 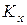через характеристики 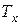. Однако реальная статистика доступна именно для округленного времени жизни 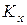, причем только для целых значений (в годах). Это связано как с удобством сбора статистических данных, так и с традиционной формой их представления в таблицах продолжительности жизни, где аргументы принимают только целочисленные значения.

Однако для расчета премий, резервов и других величин, необходимых для ведения страхового дела необходимо знать функцию выживания для всех действительных значений аргумента , а не только для целочисленных. Соответственно возникает задача определения характеристик величины 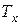, если известны характеристики величины 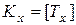(причем только для целых значений ). Для целых значений и можно абсолютно точно определить распределение 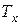через распределение :

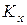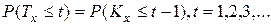
Таким образом, задача может рассматриваться как задача интерполяции. При этом достаточно рассмотреть задачу интерполяции только для функции выживания 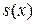(поскольку более сложные величины могут быть выражены через ).

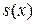В актуарной математике обычно решают эту задачу, постулируя тот или иной вид функции 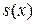между узлами интерполяции, т.е. получают искомую функцию 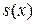, склеивая в целочисленных точках более простые функции.

Равномерное распределение смертей

Самой простой является интерполяция линейными функциями:

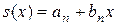при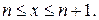

Поскольку значения 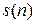и – и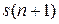звестны, из уравнений

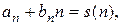
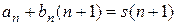
можно определить 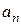и :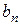

,

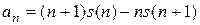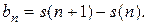
Таким образом, на отрезке 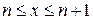функция 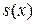приближается линейной функцией:

.

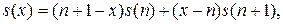
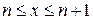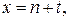Записывая в виде где 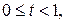этой формуле можно придать вид:

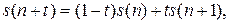
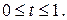
Для плотности 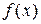это приближение дает:

.

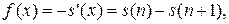
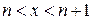Соответственно для интенсивности смертности 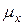мы имеем следующее приближение:

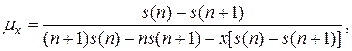
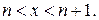
С помощью величины 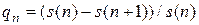(вероятность того, что человек в возрасте лет умрет в течение ближайшего года) эту формулу можно переписать виде:

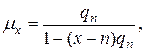
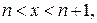
или, что то же самое,

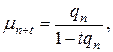
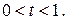
Одно из наиболее важных следствий предположения о линейной интерполяции функции выживания заключается в следующем. Рассмотрим величину 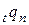( – целое, ).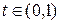

Для нее имеем:

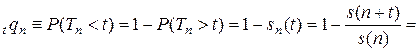
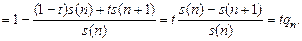
Далее, для целого и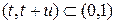

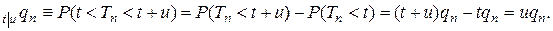
Итак, в предположении о линейной интерполяции функции выживания в течение (начальной) части года пропорциональна длине этой части (т.е. 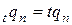), то для дробных возрастов (между двумя соседними целыми) функция выживания является линейной. Действительно, всегда верны равенства

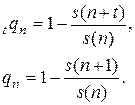
Поэтому равенство 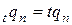влечет, что

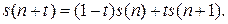
Верно и обратное утверждение, если вероятность смерти в течение (начальной) части года пропорциональна длине этой части (т.е. 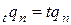), то для дробных возрастов (между двумя соседними целыми) функция выживания является линейной.

Введем теперь случайную величину 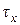, равную дробной части величины 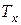: 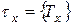. Таким образом, 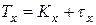, где 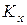– урезанное время жизни. Величина 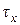описывает момент смерти внутри года.

Для рассматриваемой интерполяции

1) случайная величина 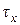равномерно распределена на ;

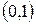2) случайные величины 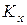и 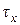– независимы.

Постоянная интенсивность смертности

Будем приближать функцию выживания 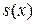на отрезке 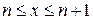показательной функцией 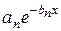. Поскольку значения 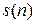и и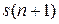звестны, из уравнений

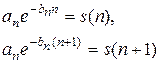
можно определить 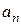и :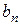

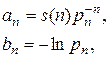
где величина 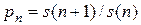– вероятность того что, что человек в возрасте лет проживет по меньшей мере один год.

Таким образом,

.

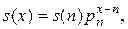
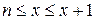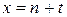Записывая в виде , где 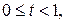этой формуле можно предать вид:

.

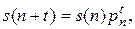
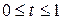Для плотности 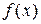это приближение даст:

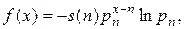
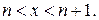
Отсюда для интенсивности смертности 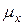мы имеем следующее приближение:

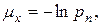
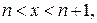
т.е. рассматриваемой интерполяции соответствует предложение о постоянной интенсивности смертности между двумя днями рождений.

Предположение Балдуччи

Предположение Балдуччи внешне похоже на предположение о равномерном распределении смертей, однако, в отличие от последнего, линейными функциями интерполируется 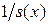. Это приводит к следующим формулам:

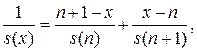
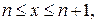
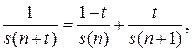
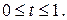
Отсюда можно получить явную формулу для 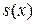на отрезке :

,

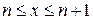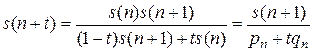где вероятност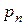и и 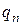были определены ранее как вероятность того, что человек в возрасте лет проживет еще по меньшей мере один год, и вероятность того, что человек в возрасте лет умрет на протяжении этого года, соответственно.

Для плотности 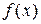это приближение дает:

.

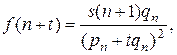
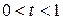Соответственно для интенсивности смертности 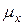имеем следующее приближение:

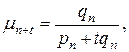
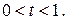
Одно из наиболее важных следствий предположения Балдуччи заключается в следующем. Рассмотрим величину 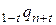( – целое, 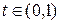). Для нее имеем:

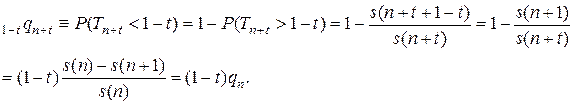
Итак, в предположении Балдуччи вероятность смерти до очередного дня рождения пропорциональна времени до этого дня рождения.

Верно и обратное утверждение, если вероятность смерти до очередного дня рождения пропорциональна времени до этого дня рождения (т.е. 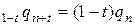), то для вида функции выживания для дробных возрастов (между двумя соседними целыми) верно предположение Балдуччи.

Резюме

В основе страхования жизни, лежит принцип распределения убытков одного лица, с которым произошел страховой случай, на большое число участников страхования, с которыми в рассматриваемый момент времени такой случай не произошел. Неопределенность момента смерти является основным фактором риска при страховании жизни. Относительно момента смерти отдельного человека нельзя сказать ничего определенного. Однако если участники страхования представляют собой большую однородную группу людей, то в этом случае применим аппарат теории вероятностей как науки о массовых случайных явлениях, обладающих свойством устойчивости. Поэтому в актуарной математике в качестве исходной случайной величины рассматривают продолжительность жизни, а также связанные с этой величиной основные функции и характеристики.

Во многих случаях для упрощения расчетов и теоретического анализа эмпирические функции выживания или интенсивности смертности описывают с помощью рассмотренных аналитических законов.

Поскольку страховая компания имеет дело с конкретными людьми, дожившими до определенного возраста, то обычно рассматривают не продолжительность жизни, а остаточное время жизни, а также связанные с этой величиной основные функции и характеристики.

Статистические данные о продолжительности жизни суммируются в таблицах продолжительности жизни. Рассмотрены следующие виды таблиц продолжительности жизни: таблицы, содержащие информацию о статистических свойствах времени жизни случайно выбранного человека, относительно которого известен только его возраст; таблицы отбора риска – таблицы продолжительности жизни для различных групп населения; таблицы с отбором ограниченного действия, поскольку зависимость характеристик смертности от времени, прошедшего с момента отбора, быстро уменьшается.

Для расчета премий, резервов и других величин, необходимых для ведения страхового дела необходимо знать функцию выживания для всех действительных значений аргумента. Однако реальная статистика доступна для округленного времени жизни 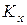, причем только для целых значений (в годах). Это связано как с удобством сбора статистических данных, так и с традиционной формой их представления в таблицах продолжительности жизни, где аргументы принимают только целочисленные значения. Соответственно возникает задача определения характеристик величины остаточного времени жизни, если известны характеристики величины округленного времени жизни. Для решения поставленной задачи было рассмотрено три вида интерполяции дробных возрастов.

Вопросы для самопроверки

1. Функция выживания. Определение, свойства.

2. Кривая смертей. Интенсивность смертности.

3. Макрохарактеристики продолжительности жизни.

4. Аналитические законы смертности.

5. Остаточное время жизни. Основные величины, связанные с остаточным временем жизни.

6. Округленное время жизни. Основные величины, связанные с округленным временем жизни.

7. Таблицы продолжительности жизни. Виды таблиц, основные характеристики таблиц.

8. Интерполяция для дробных возрастов: равномерное распределение смертей; постоянная интенсивность смертности; предположение Балдуччи.