Примеры функциональных пространств

Наиболее важным отличием между различными пространствами функций является вид введенной нормы, хотя это и не единственное различие. Все интересующие нас банаховы пространства функций строятся единообразным способом. Выбирается исходное пространство функций, на нем определяется вид нормы и далее к этому множеству присоединяются все пределы всех фундаментальных последовательностей. Осуществляется его пополнение. Получаемое нормированное пространство по построению оказывается полным, т.е. банаховым, а исходное множество - плотным в нем подмножеством. Конечно, в зависимости от введенной нормы состав элементов в получаемых пространствах различен, но главным для нас является различие в выражениях для нормы. Введение различных пространств продиктовано необходимостью конкретного выражения для нормы, а не «нехваткой» элементов пространств для тех, либо иных, описаний. Приведем пример.

Простейшим и одновременно наиболее употребляемым из всех рассматриваемых банаховых пространств является гильбертово пространствоL₂ (V), состоящее из всех квадратично интегрируемых в области V функций с нормой:

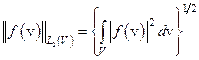
Оно выделяется по своим свойствам в связи с тем, что для любых двух элементов 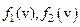определен линейный непрерывный функционал

,

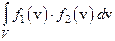называемый скалярным произведением. Скалярным произведением исчерпываются все линейные ограниченные функционалы на с. В соответствии с теоремой Риса этим и устанавливается то, что двойственным к L₂(V), которое мы отождествляем с сопряженным, служит само L₂(V). Другим распространенным банаховым пространством служит С(V), состоящее из всех непрерывных в области V функций с нормой

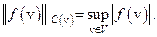
Множество L₂(V) и С(V) не совпадают, хотя их пересечение плотно, как в L₂ (V), так и в С(V). Для практических целей - описания объектов, возникающих в геофизических приложениях - наблюдаемых распределений физического параметра, хватило бы и этого пересечения. Но мы рассматриваем 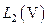, либо С(V) в связи с тем, что основной в этой книге часто рассматривается задача оптимизации вида:

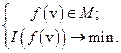
Для ее решения желательно, чтобы функционал 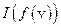имел вид нормы. Далее множество М часто представлено как 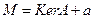, где заданный линейный оператор и 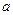элемент (функция) из его области определения. Для существования решения этой оптимизационной задачи требуется, чтобы множество М было замкнутым относительно функционала 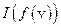. Последнее означает, что этот функционал, рассматриваемый как оператор из М во множество вещественных чисел, должен быть на множестве М замкнутым. Если 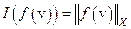, то для выполнения этого требования достаточно, чтобы А был непрерывен (при условии, что он линеен) на функциональном пространстве Х. Такого рода потребности и вынуждают рассматривать не только простейшие – гильбертовы пространства, которых по числу элементов, несомненно, хватает, но и более сложные и общие – пространства Банаха.

Обозначим 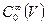- множество всех непрерывных и бесконечно дифференцируемых функций, образующихся в ноль на границе ∂V области V. На множестве 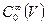введем норму:

.

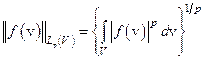Здесь 1≤p<∞. Пополним 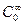относительно введенной нормы. В результате получим банахово пространство, обозначаемое 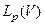. При p=2 получим уже упоминавшееся ранее гильбертово пространство L₂(V). Для случая p=∞:

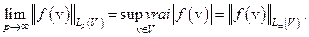
Здесь: “ 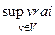” означает “существенная верхняя грань”, т.е. верхняя грань по множеству V, за исключением, может быть множества меры нуль (т.е. конечного или счетного числа точек из V). Пополнение 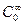по такой норме образует банахово пространство L_∞(V).

Пространство 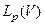состоит из всех функций с конечной величиной 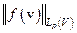. Иными словами, любая функция с конечной величиной 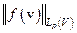может быть представлена как предел в норме 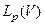последовательности элементов из .

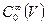Всякий линейный ограниченный функционал на 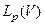имеет вид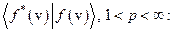

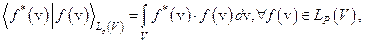
где 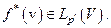Причем .

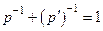Норма этого функционала в точности равна норме элемента 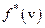, порождающего этот функционал в соответствии с теоремой Риса, и несколько условно можно записать:

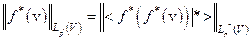
Таким образом, сопряженное к 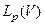пространство изометрически изоморфно пространству 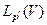. Последнее означает, что каждому элементу 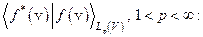соответствует один и только один элемент 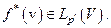Так, что

.

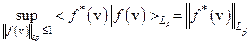В смысле этого изоморфизма и отождествляются 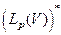и _.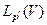

Из приведенного факта следует, что 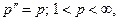так, что 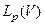- рефлексивно. Отсюда, в частности, следует и другой вывод. Поскольку

,

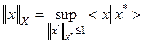то: .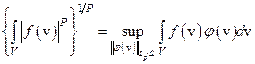

Банахово пространство называется сильновыпуклым, если для 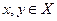, из условий 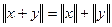следует 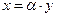, где α - число. Это определение совпадает с данным ранее для топологических пространств, в случае топологии нормы.

Банахово пространство называется равномерновыпуклым, если из того, что 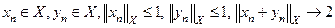следует .

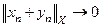Равномерновыпуклые пространстваодновременно и сильновыпуклы.

Пространства 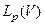(1<p<∞) являются равномерновыпуклыми и каждое равномерно-выпуклое пространство рефлексивно. Однако существуют рефлексивные пространства, не являющиеся равномерновыпуклыми.

Пространство L₁(V) и L_∞(V) не являются ни равномерновыпуклыми, ни рефлексивными. При этом сопряженным к L₁(V) служит L_∞(V) (в смысле указанного выше изометрического изоморфизма). Сопряженное к L_∞(V) образует специальное множество функций, которое обозначается ba, а нормой служит полная вариация. Пространство L₁(V) образует *- слабо плотное множество в ba и, таким образом, ba можно рассматривать как * - слабое замыкание L₁(V). Это обстоятельство нам потребуется в гл.7.

В связи с пространствами L_p важен результат, называемый теоремой Рисса о выпуклости. Мы приведем лишь один его частный случай.

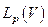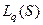Теорема Риса о выпуклости.Пусть А – линейное ограниченное отображение из в и 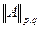- его норма. Пусть известно, что 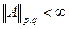для всех комбинаций p, q={0, 0; 0, 1; 1, 0; 1, 1}. Тогда 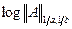- есть выпуклая функция от а, b при 0≤a, b≤∞.

Эта теорема позволяет делать вывод об ограниченности оператора в нормах промежуточных пространств, если известна его ограниченность в пространствах с индексами 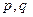равными 0 и 1.

Следующее неравенство известно, как

Неравенство Юнга. Пусть 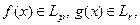где 1/p+1/r≥1, p≥1, r≥1. Тогда, для

,

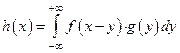имеем

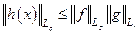
при

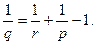
Пространство 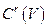является замыканием (пополнением) 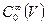относительно нормы:

,

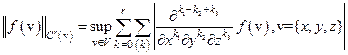где 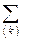означает суммирование по всевозможным комбинациям индексов 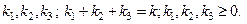Это пространство состоит из функций, непрерывных в V вместе со всеми своими производным до порядка r включительно (по любому из аргументов). Легко увидеть, что если 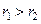, то 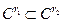. Наиболее распространен случай - 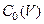, обозначаемый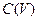

.

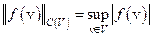Пространство 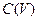не является ни рефлексивным, ни сильновыпуклым, и общий вид линейного функционала над C(V) имеет вид

,

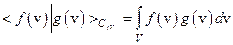где 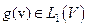. Так что L₁(V) можно отождествлять (в смысле изометрического изоморфизма) с .

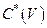Соболевское пространство 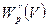состоит из пополнения 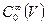по норме:

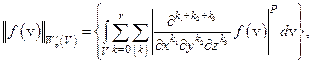
Для этого пространства не потребуется строить ему сопряженное, конструкция которого требует введения дополнительных понятий (пространства с отрицательной нормой по Лаксу). Важно лишь отметить, что единичная сфера в 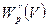компактна в L_p(V).

Обобщением конечномерных пространств 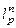, рассмотренных в приложении 1 служат множества, состоящие из сходящихся бесконечных числовых последовательностей 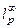, которые будем обозначать 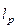. Пространства 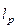определяются как пространства числовых последовательностей пронумерованных натуральным числовым рядом; 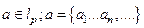и:

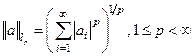
Для p=∞: .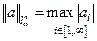

Сопряженное к 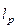пространство изометрически изоморфно 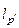, и общий вид линейного ограниченного функционала на 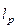задан соотношением

.

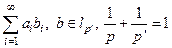Все 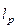рефлексивны.

В качестве примера использования пространства 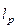построим сопряженный к оператору из 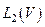в .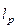

Оператор, аналогичный (2), в практических случаях приходится рассматривать с областью значений в 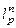. Приводимые ниже соотношения более общие, относятся к 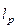и легко распространяются на случай 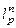. Это соответствует случаю, когда наблюдаемый гравитационный эффект измерен в в конечном числе n точек 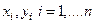. Для 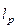число этих точек счетное.

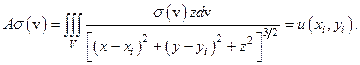
Будем считать, что 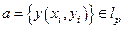. Поскольку 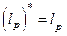, то для 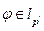имеем:

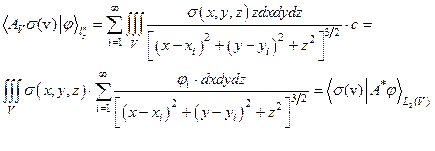
Таким образом, в случае такого задания оператора А, А^*φ отождествляется с отображением из 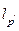в 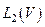по правилу:

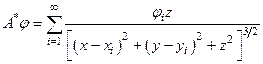
Экстремальные задачи

При решении обратных задач геофизики вариационные методы занимают ведущее место. Задачи на максимум или минимум, а в общем случае - задачи на нахождение экстремума, пронизывают все постановки и методы, используемые при анализе геофизической информации. Они являются главным средством для решения обратных задач, на их основе реализуется содержательная постановка задач. Это становится понятным, если вспомнить, что наблюдаемая компонента геофизического поля, подлежащая обработке и интерпретации, осложнена ошибками. Задачи анализа данных состоят чаще всего в наилучшей аппроксимации (подборе) этой наблюдаемой системой заданных элементов, образующих заданное множество 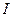. Наилучший подбор достигается тогда, когда невязка между наблюдаемой и искомым элементом из 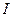становится минимальной. Если мера удаления наблюдаемой 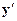от произвольного 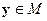оценивается функционалом 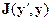, то задача обработки данных сводится к:

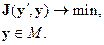
Например, это может выглядеть так:

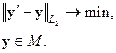
Рассмотрение такого рода задач составляет предмет теории экстремальных задач. Рассмотрим один достаточно простой пример.

Искомой является функция двух переменных, доставляющая минимум функционалу:

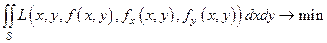(2.10)

Здесь 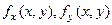обозначают, соответственно производные функции по х и у; S - область в R², L - некоторая функция, в данном случае, пяти переменных, которая в приложениях называется Лагранжевой плотностью. Это переменные 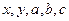, где вместо переменных 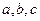подставлены 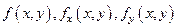соответственно. Предположим, что решение задачи (10) существует и есть . Предположим, далее, что функция 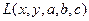достаточное число раз дифференцируема по всем своим переменным. Пусть 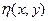- произвольная непрерывно-дифференцируемая функция, заданная в S и равная нулю на границе ∂S области S. Тогда

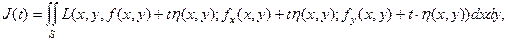[38] (2.11)

Где t - числовой параметр, есть обычная функция переменной t. Поскольку экстремум (10) достигается на , то экстремум (11) достигается при t=0. Тогда производная от (11) должна обращаться в нуль при t=0:

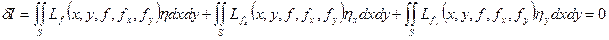
Здесь 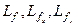- производные от функции 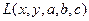по 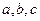соответственно, на место которых подставлены 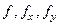. Далее

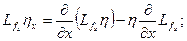
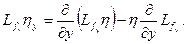
Тогда:

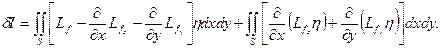
Второй интеграл, после применения формулы Грина, равен:

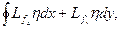
и обращается в нуль, поскольку значения 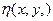равны нулю на ∂S по условию. Тогда равенство:

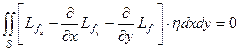
выполняется для всех 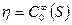. С другой стороны, 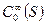плотно в L₂(S). Следовательно:

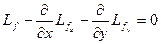. (2.12)

Это и есть искомое уравнение Эйлера, являющееся необходимым условием, которому удовлетворяет экстремаль (т.е. решение вариационной задачи) (10).

В том случае, когда на искомую экстремаль наложены дополнительные ограничения вида:

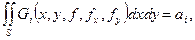(2.13)

задача минимизации функционала (10) при условии (13) сводится к безусловной минимизации (т.е. минимизации рассмотренного выше вида) функционала:

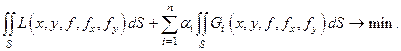(2.14)

Здесь 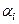- числа, которые называются множители Лагранжа. Это правило – замена задачи на условный экстремум (10,13) задачей на безусловный экстремум (14) называется «правило Лагранжа".

Числа 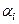– находятся из условия, чтобы экстремаль (14) удовлетворяла системе уравнений (13).

Предполагается, что 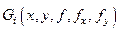также требуемое число раз дифференцируема по всем своим аргументам.

В приведенном примере мы столкнулись с тем обстоятельством, что отображение 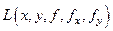следовало дифференцировать по функциям, как по переменным. Таковы производные 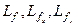. Это характерное обстоятельство. Введем соответствующее определение.

Пусть Х,Y – банаховы пространства, и А(х) - отображение (оператор) окрестности Q(х) точки 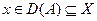в 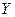. 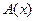называется дифференцируемым по Фреше (сильно- дифференцируемым) в точке , если существует такой линейный непрерывный оператор, 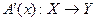А, что

,

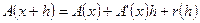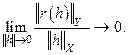
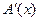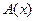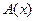называется производной Фрешеоператора в точке . Если оператор - дифференцируем по Фреше в окрестности точк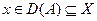и , и 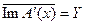, то А - регулярен в окрестности х. Следует помнить, что 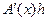суть линейный оператор, действующий на элементы 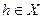. Если для всех точек из Q(х) существует 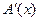и отображение 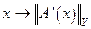непрерывно, то 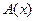называется непрерывно-дифференцируемым или отображением (оператором) класса .

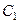Наряду с производной Фреше и следующими из нее понятиями, можно ввести и другое определение - производную Гато или слабую производную. Далее используется только сильная производная, поэтому термин «Фреше» зачастую опускается.

Благодаря введенному понятию, оправдывается дифференцирование некоторого отображения по функции, как по переменной. Так собственно и вычисляются производные. Рассмотрим пример.

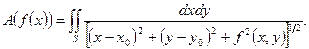
Это отображение можно рассматривать из подмножества в 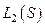функций, таких что 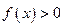. Для того, чтобы вычислить производную Фреше, продифференцируем это выражение по 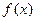, как по параметру. В результате получим:

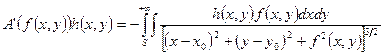
Пусть 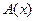- линейный оператор: 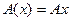.Тогда 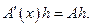Производная уже не зависит от , оператор действует на приращение 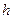, следовательно, во всех точках х производная одна и та же. Следует всегда помнить, что производная - это линейный оператор, действующий из Х в Y.

Следующая теорема называется правилом (принципом) Лагранжа и является основной в вариационном исчислении. Она является обобщением того приема, который был введен под тем же названием выше (задачи (10,13,14)).

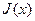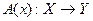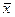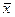Правило Лагранжа.Пусть функционал и отображение дифференцируемы по Фреше в окрестности точки , где - решение задачи:

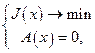
существование которого предполагается. Пусть 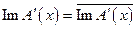. Тогда найдутся не равные одновременно нулю элементы 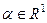и 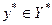, такие, что:

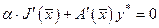. (2.15)

Если 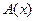непрерывно-дифференцируемо и регулярно в точке 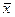, то 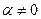, и можно считать, что .

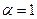Уравнение (15) называется уравнением Эйлера-Лагранжа.

Доказательство этого результата см. [А.Д.Иоффе, В.М.Тихомирова, стр.87-88]. Здесь, как и для уравнения (12), приведем лишь пояснения к результату.

Пусть 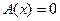. Построим вариацию 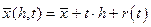такую, что

,

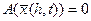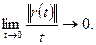
Тогда:

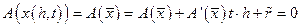
Где 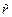- величина более высокого порядка малости, чем остальные члены,. Отсюда заключаем, что 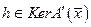. В условиях теоремы, т.е. в предположении замкнутости 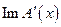непрерывности отображения 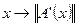в окрестности точки 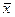, имеет место и обратное утверждение: совокупность векторов 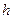из 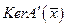обладает свойством:

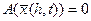
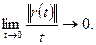
Теперь рассмотрим функцию параметра t:

.

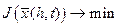По условию ее минимум должен достигаться при t=0 и, следовательно, вычисляя производную по t при t=0:

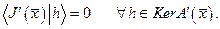
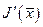- есть линейный функционал над Х, и его мы записали для наглядности в виде 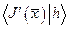. Элемент 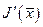, таким образом, отождествляется в смысле изометрического изоморфизма с некоторым элементом из Х^*. Из последнего условия, по теореме о ядре 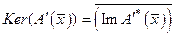, получаем 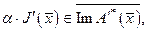где - некоторое число[39]. Следовательно, в регулярном случае 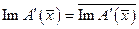, откуда следует, 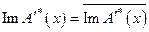существует элемент 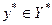и 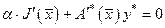. Это и требовалось показать.

Здесь важно отметить то, что требование регулярности оператора 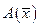в окрестности точки 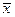является весьма жестким. И хотя, фактически, результат теоремы чаще всего справедливым остается и когда 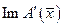незамкнуто, строгое ее применение неправомерно. Из замкнутости 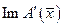следует корректная разрешимость факторизованного уравнения

,

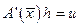которая называется нормальной разрешимостью.

Последнее означает корректную разрешимость уравнения относительно фактор пространства пространства Х по ядру оператора, или корректность решения задачи

,

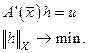Зачастую при постановках обратных геофизических задач нормальная разрешимость места не имеет. Так, например, приведенный результат нельзя применять к задаче:

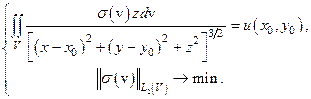
Приведенный выше результат - теорема Лагранжа (принцип Лагранжа) - это необходимые условия экстремума. Для его корректного применения следует еще доказать, что соответствующая конкретная задача имеет решение и записанные условия достаточны. Доказать это удается, как правило, лишь в весьма жестких предположениях относительно функционала и оператора 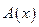. Оказывается, что для специальных случаев, к которым могут быть сведены многие геофизические задачи, соответствующие результаты можно доказать, исходя из других принципов, не используя производных.

В большинстве рассматриваемых в приложениях случаях, функционал имеет специальный вид - вид нормы в банаховом пространстве. Рассмотрим следующую задачу, называемую задачей о наилучшем приближении.

Пусть Х – банахово пространство, М – его подмножество и х₀ - элемент из Х, не принадлежащий М. Назовем элемент 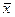наилучшим приближением к х₀ (аппроксимацией х₀) на множество М, если

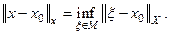(2.16)

Для того чтобы такой элемент существовал всегда, необходимо, чтобы М было замкнуто. Следующая цепочка результатов характеризует условия существования и единственности решения задачи (16).

Пусть М - замкнутое множество в банаховом пространстве Х (например, М - подпространство). Тогда решение 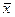задачи (16) существует. Если М дополнительно выпукло, то множество решений задачи (16) образует замкнутое выпуклое множество, если пространство Х дополнительно сильно выпукло (например, равномерно-выпуклое), то решение задачи (16) единственно. Напомним, что равномерно-выпуклые пространства являются сильновыпуклыми. Сюда относятся все пространства L_p при 1<p<∞.

Наиболее типичными примерами задач, рассматриваемых далее, являются следующие:

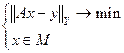(2.17)

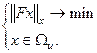(2.18)

Здесь А, F - некоторые операторы, М, Ω_u- подмножества в банаховом пространстве Х. Задача (17) возникает при подборе параметров модели среды из класса моделей М по требованию наилучшего согласия наблюдаемой у и рассчитанной от элемента х по правилу Ах поля.

Теорема 4. Если 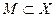– замкнутое выпуклое множество, Х – рефлексивно, Y – сильно выпукло (Х,Y - банаховы пространства). А: Х→Y – взаимнооднозначен и непрерывен, то решение задачи (17) существует и единственно.

Доказательство*. При доказательстве этого результата существенно используется понятие слабой топологии.

Поскольку М - замкнуто и выпукло, Х - рефлексивно, то М - слабокомпактно. Поскольку А - непрерывен, то и слабонепрерывен, следовательно, слабокомпактные множества переводит в слабокомпактные. Таким образом, оказывается, что S - образ М при отображении А является слабозамкнутым. Поскольку в силу выпуклости М выпукло и S, то множество S будет замкнуто сильно (слабозамкнутое выпуклое множество сильнозамкнуто).

Следовательно, решение задачи:

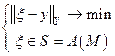(2.19)

существует и единственно, поскольку минимум сильно выпуклого функционала на замкнутом выпуклом множестве достигается и единственен. Обозначим его 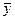. Поскольку А - взаимнооднозначен на М, и 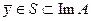, то существует единственный элемент 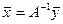, являющийся решением (17). Что и требовалось доказать.

Задача (19) – это преобразованная задача (17), и она по форме аналогична (16). Это второе обстоятельство, которое мы хотели проиллюстрировать.

Обозначим 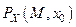оператор, ставший в соответствие элементу 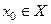решением задачи (16). Тогда решение задачи (19) суть 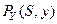и решение задачи (17) можно представить в виде:

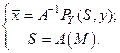(2.20)

Если А - взаимнооднозначен, непрерывен и М - компактно, то, в соответствии с теоремой о гомеоморфизме (20), оказывается непрерывным. Рассмотрения, развивающие приведенные, имеются в п.3.2 и составляют теоретическую основу методов квазирешений.

Рассмотрим теперь задачу (18), предполагая, что

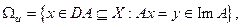
где А - линейный ограниченный оператор из Х в Y (Х,Y- банаховы пространства). Ω_u есть сдвиг КerA и, в силу непрерывности А, КerA замкнуто в Х. Следовательно, замкнуто и выпукло Ω_u. Если F- гомеоморфизм, то образ Ω_u при отображении F есть также замкнутое выпуклое множество. Тогда задача (18) записывается в эквивалентной форме:

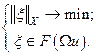(2.21)

Решение (18) есть 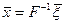, где - решение (21). Таким образом, и (17), и (18) сводятся к задаче (16).

Следующий результат касается задачи (16) и является для нее основным.

Теорема двойственности. Пусть М - замкнутое выпуклое множество линейного нормированного пространства Х. Для того, чтобы элемент 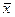был наилучшим приближением в М к х₀, т.е. являлся решением задачи:

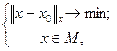(2.22)

необходимо и достаточно, чтобы в сопряженном к пространстве Х^* существовал элемент 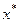, определяющий линейный функционал на 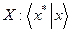такой, что:

а)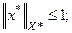

б) 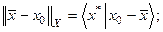(2.23)

в) .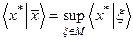

Условие (в) в приведенном результате может быть, как это нетрудно видеть, заменено эквивалентным

в’)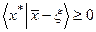

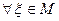
В том частном случае, когда М – линейное подпространство в Х, условие (в), либо ему эквивалентное (в’), заменяется на

в’’)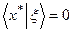

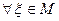
Действительно, если предположить возможность строгого неравенства в (в’), то в силу линейности М, оно всегда может быть обращено для некоторого другого ξ, и, следовательно, возможно только равенство.

Приводимое ниже следствие из теоремы двойственности является одним из главных результатов, используемых в гл.5,7.

Следствие. Если А – линейный ограниченный оператор из Х в Y, где Х,Y- банаховы пространства и

,

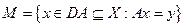то условие (в) в теореме двойственности заменится на

в’’’)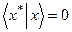

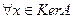
Докажем этот результат.

Пусть 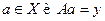. Тогда 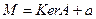и

.

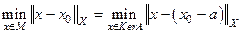Решение задачи (23) есть 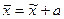, где 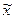- решение задачи

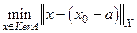(2.24)