Основные числа теории графов

1. Хроматическое число графа.
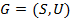– неориентированный граф без петель.
Граф 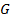называется правильно раскрашенным, если каждой его вершине приписан какой-либо цвет, а две соседние вершины окрашены в разные цвета. Минимальное число цветов, в которое может быть окрашен правильно раскрашенный граф, называется хроматическим числом графа . Если , тогда 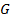называют хроматическим.
Теорема: для того, чтобы связный неориентированный граф без петель являлся бихроматическим необходимо и достаточно, чтобы он не содержал простых циклов нечетной длины.
Доказательство:
I Необходимость
Пусть 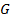– бихроматический.
Предположим противное: пусть в нем содержится простой цикл нечётной длины

Получено противоречие.
II Достаточность
Пусть 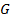не содержит простых циклов нечетной длины
Удаляем ребра в циклах так, чтобы удалить циклы и граф 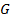стал деревом
- бихроматический
В силу четности циклов вершины, которые соединяют удалённые ребра, буду окрашены в разные цвета. И поэтому правильная раскраска графа не нарушится. ч.т.д.
Рассмотрим некоторую вершину 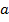. Через обозначим степень вершины, то есть число инцидентных ей ребер (если при это вершина содержит петлю, то считаем её дважды).



Если стеки всех вершин графа чётные, то граф называют чётным.
Через обозначим наибольшую из степеней вершин графа.
Тогда справедлива Теорема:
Для любого неориентированного графа справедлива следующая оценка: .
Определение: плоским называется граф, вершины которого являются точками плоскости, а ребра – непрерывными плоскими линиями без самопересечения, такими, что никакие 2 ребра не имеют общих точек, кроме инцидентных или общих вершин.
Любой граф изоморфный плоскому называют планарным графом.
Гипотеза: всякий планарный граф можно раскрасить не более чем 4 красками.
Если окрашены уже вершины , то новые произвольно взятые вершины мы приписываем минимальный из цветов, в который не окрашены соседние с ней вершины.

2. Число внутренней и внешней устойчивости.
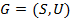- ориентированный граф.
Рассмотрим

Подмножество вершин J называется внутренне устойчивым, если J , то есть множество J не содержит соседние вершины.
Числом внутренней устойчивости графа 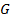называется
J - максимальная мощность внутренней устойчивости
Подмножество E вершин графа называется внешне устойчивым множеством, если E

3. Цикломатическое число графа

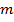- число дуг, 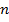– число вершин, - число компонентов связности

Транспортные сети.

Говорят, что задана транспортная сеть, если заданы 2 объекта:

v Ориентированный связный граф 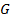, обладающий следующими свойствами

Ø 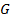не содержит циклов

Ø - источник, не имеющая предшественников,

Ø – сток, не имеющая последователей,

v Функция , действующая из множества дуг в расширенный натуральный ряд, ,
- пропускная способность дуги.

– множество дуг, входящих в

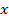
– множество дуг, исходящих из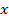

Функция , называется потоком, если

·

· справедливо условие баланса

·

Тогда величина

- величина потока

Поток 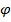называется максимальным, если его величина .

Величина - остаточная пропускная способность дуги 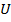, если , дуга называется насыщенной; а поток 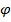, из которого каждый путь, идущий из 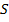в содержит хотя бы одну насыщенную дугу называется полным потоком.

Рассмотрим некоторое подмножество вершин графа .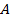

Множество дуг, начало которых лежит в множестве 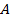, а концы в множестве , называется ориентированным разрезом:

– разрез

Пропускной способностью (величиной) разреза называется

Сам разрез , называется – разрезом, если .

– разрез называется минимальным, если его пропускная способность меньше любого – разреза

Теорема: пусть множество вершин , тогда для любого потока 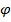справедливо:

Доказательство: докажем, что величина потока для любого разреза есть

Рассмотрим тогда справедливо условие:

Включим 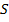, прибавка только в первую сумму на величину потока:

Если начальная и конечная вершина дуги графа принадлежит множеству 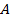, то потоки по этим дугам учитываются в первой и второй суммах, и поэтому взаимно уничтожаются, откуда и следует искомое соотношение:

Следствие:

1) Теорема Форда Фалкерсона:
Если для некоторого потока и разреза выполняется равенство:
, то , .

2) Если для некоторого потока 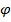и – разреза выполняется

все дуги, входящие в этот разрез должны быть насыщенными,
и наоборот.

Доказательство: 1) пусть - максимальный поток, - величина данного потока, необходимо найти разрез равный . Докажем, что существует такой разрез: .

Строим множество :

1)разрез должен быть – разрезом, поэтому

2)если вершина попала в

2а) и есть дуга , по которой , то тогда

2б) и причём , то .

Покажем, что разрез является – разрезом:

по условию, покажем, что .

Предположим противное: пусть попала в , тогда существует путь (цепь) из 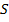в , все вершины которого лежат в , тогда рассмотрим 2 соседние вершины (все пары) и . Для всех дуг, соединяющие эти вершины, посчитаем:

Теперь в качестве и построим другой поток.

Поток по каждой прямой дуге, попавшей по причине 2а увеличим на , по причине 2б – уменьшим на .

Тогда мы построим новый поток, условие баланса не нарушено:

Получено противоречие.

Покажем, что величина разреза совпадает с величиной потока. Рассмотрим дуги - лежащие в разрезе:
1) , если согласно 2а - противоречие.
– насыщенная.

2) , , согласно 2б - противоречие,
для всех вершин.

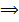по теореме